В настоящее время информация передается по каналам связи в основном в цифровой форме. Числа при передаче с периодом Т поступают от источника информации и называются символами (symbol), а частота передачи символов – символьной скоростью
(symbol rate) fT=1/T. В практике передачи данных распространена двоичная (binary) последовательность символов, где числа передаются значениями 0 и 1.Символьные последовательности являются дискретными квантованными сигналами, которые обычно передаются следующим образом. Каждому из возможных символов устанавливается определенный набор параметров несущего колебания, которые поддерживаются постоянными на интервале Т до прихода следующего символа. Это означает преобразование последовательности чисел в ступенчатый сигнал (кусочно-постоянная интерполяция) который используется в качестве модулирующего сигнала. Соответственно, параметры несущего колебания, на которые переносится ступенчатый сигнал, также меняются скачкообразно. Такой способ модуляции несущей называется манипуляцией (keying), и может выполняться с использованием всех рассмотренных методов модулирования.
Амплитудно-манипулированные сигналы
простейшего типа представляют собой последовательности радиоимпульсов, разделенные паузами. Такие сигналы используются в радиотелеграфии и в системах передачи дискретных данных. Форма огибающей радиоимпульсов в общем случае может быть произвольной, паузы могут отличаться по длительности от радиоимпульсов.На рис. 9.5.1. приведен пример амплитудно-манипулированного сигнала:
u(t) = UmЧ cos(2pfot),
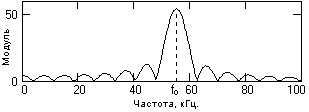
Рис. 9.5.1. АМП-сигнал. Рис. 9.5.2. Модуль спектра АМП-сигнала.
с прямоугольной П-формой огибающей. Соответственно, в частотной области спектр АМП – сигнала образуется сверткой спектра огибающей функции (в данном случае – спектра прямоугольного импульса) со спектром косинусного колебания (дельта - функции на частоте f
o). Модуль спектральной плотности сигнала приведен на рис. 9.5.2. Спектр прямоугольного импульса довольно слабо затухает и простирается неограниченно далеко, а поэтому его использование в качестве огибающей АМП - сигнала не рекомендуется, хотя и является наиболее простым по техническому исполнению.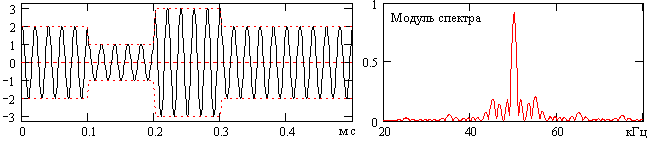
Рис. 9.5.3. Рис. 9.5.4.
На рис. 9.5.3. приведен пример формы классического АМП сигнала при передаче нескольких символов, каждому из которых соответствует индивидуальная амплитуда несущей частоты при постоянной длительности интервалов посылки. Модуль спектра сигнала приведен на рис. 9.5.4 и тоже имеет достаточно большую ширину значимой части спектра вокруг несущей частоты.
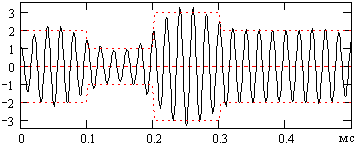
Естественно, что при передаче данных частотный диапазон канала передачи данных ограничивается значимой частью спектра, ширина которого устанавливается по допустимой степени искажения приемных сигналов. Степень искажения сигналов существенно зависит от длительности посылок. Пример искажения вышеприведенного сигнала при ограничении спектра интервалом 40-60 кГц приведен на рис. 9.5.5.
Угловая манипуляция, как правило, использует частотные методы модулирования, в которых каждому возможному значению передаваемого символа сопоставляется индивидуальное значение частоты гармонической несущей. При этом в точках сопряжения интервалов посылок могут происходить скачки напряжения, с соответствующим усложнением спектра модулированного сигнала. Самый простой способ – синусоидальное начало несущей на каждом интервале с кратным количеством периодов несущей в посылке. При более сложных способах, независимых от точного сопряжения несущих частот с интервалами посылок, осуществляется управление скоростью изменения фазы несущих на границах посылок.
Демодуляция сигналов осуществляется корреляционными методами. Сущность методов – вычисление взаимной корреляции между принимаемым сигналом и набором опорных частот, используемых при модулировании, с идентификацией символов по максимумам взаимной корреляции.
Для повышения помехоустойчивости передачи данных желательно, чтобы разносимвольные посылки были некоррелированны. Если для бинарных символов 0 и 1 принять частоты посылок равными
s0(t) = cos wo(t), s1(t) = cos w1(t),
то их ВКФ при нулевом временном сдвиге определится выражением:
B01(0) =
s0(t) s1(t) dt = Ѕ (sin (ω1+ωo)T)/(ω1+ωo) + Ѕ (sin (ω1-ωo)T)/(ω1-ωo).
При (ω
1+ωo)T >> 1 первым слагаемым можно пренебречь, оно много меньше второго. А второе слагаемое обращается в нуль при (ω1+ωo)T = πk, где k = 1, 2, ... – целое число. Отсюда, минимальное значение между частотами манипуляции для некоррелированных посылок определяется выражениями:D
ωmin = p/T, Dfmin = 1/2T = fT/2,где f
T – символьная скорость.Фазовая манипуляция применяется значительно реже, в связи со значительными сложностями измерения абсолютных значений начальных фаз в посылках. Проще определяется относительный фазовый сдвиг в соседних посылках, поэтому обычно используется фазоразностная манипуляция.
литература
1. Баскаков С.И. Радиотехнические цепи и сигналы
: Учебник для вузов.- М.: Высшая школа, 1988.2. Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2003. – 608 с
.
|
|
 |
