Внутриимпульсная частотная модуляция

Сигнал с внутриимпульсной частотной модуляцией – это радиоимпульс, высокочастотное заполнение которого имеет переменную частоту.

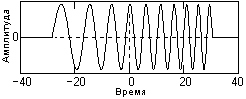
ЛЧМ – сигналы. Если закон изменения мгновенной частоты заполнения имеет линейный характер, то такие сигналы носят название ЛЧМ – сигналов (линейная частотная модуляция). Наиболее широкое применение они получили в радиолокации. Пример ЛЧМ – сигнала с огибающей прямоугольной формы приведен на рис. 9.3.1.

ЛЧМ – сигналы имеют одно замечательное свойство. Если сигнал подать на частотно-зависимую линию задержки, время задержки сигнала которой велико на малых частотах (в начальной части ЛЧМ – сигнала) и уменьшается по мере нарастания частоты в ЛЧМ – сигнале, то на выходе такой линии происходит "сжатие" сигнала в один период высокочастотного колебания путем суммирования амплитудных значений всех периодов сигнала. При этом происходит увеличение амплитуды выходного сигнала и уменьшение статистических шумов, так как суммируемые одновременно по этим же периодам шумы не коррелированны.

Для модели радиоимпульса с прямоугольной огибающей примем его длительность равной t_и, и точку t = 0 поместим в центр радиоимпульса. Допустим также, что частота заполнения линейно нарастает от начала импульса к его концу со скоростью m (с^-2), при этом:

w(t) = w_o + mt. (9.3.1)

Девиация частоты за время длительности импульса и полная фаза сигнала:

Dw = mЧ t_и. (9.3.2)

y(t) = w_ot + mt²/2. (9.3.3)

Уравнение ЛЧМ – сигнала:

u(t) = 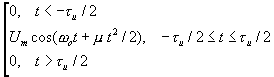(9.3.4)

Спектр прямоугольного ЛЧМ – сигнала вычисляется через преобразование Фурье. Девиация частоты за время длительности импульса по сравнению с несущей частотой обычно мала (Dw << w_o) и форма спектра зависит от так называемой базы импульса:

DwЧ t_и = mЧ t_и². (9.3.5)

На рис. 9.3.2 приведен пример формы спектральной плотности ЛЧМ – сигнала при малом значении базы в области несущей частоты сигнала.

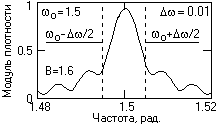
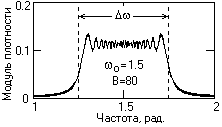
Рис.9.3.2. Спектр ЛЧМ- сигнала. Рис. 9.3.3. Спектр при B>>1.

На практике значение базы сигналов обычно много больше 1. Увеличение базы сопровождается расширением полосы спектра Dw, при этом в пределах этой полосы модуль спектральной плотности практически постоянен и равен U_mЧ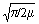. Пример спектра приведен на рис. 9.3.3.

к оглавлению

Знаете ли Вы, что низкочастотные электромагнитные волны частотой менее 100 КГц коренным образом отличаются от более высоких частот падением скорости электромагнитных волн пропорционально корню квадратному их частоты от 300 тысяч кмилометров в секунду при 100 кГц до примерно 7 тыс км/с при 50 Гц.

НОВОСТИ ФОРУМА

Рыцари теории эфира