Дискретизация сигналов и функций
Введение
В первой половине ХХ века при регистрации и обработке информации использовались, в основном, измерительные приборы и устройства аналогового типа, работающие в реальном масштабе времени, при этом даже для величин, дискретных в силу своей природы, применялось преобразование дискретных сигналов в аналоговую форму. Положение изменилось с распространением микропроцессорной техники и ЭВМ. Цифровая регистрация и обработка информации оказалась более совершенной и точной, более универсальной, многофункциональной и гибкой. Мощь и простота цифровой обработки сигналов настолько преобладают над аналоговой, что преобразование аналоговых по природе сигналов в цифровую форму давно стало производственным стандартом.
Под дискретизацией сигналов понимают преобразование функций непрерывных переменных в функции дискретных переменных, по которым исходные непрерывные функции могут быть восстановлены с заданной точностью. Роль дискретных отсчетов выполняют, как правило, квантованные значения функций в дискретной шкале координат. Под квантованием понимают преобразование непрерывной по значениям величины в величину с дискретной шкалой значений из конечного множества разрешенных, которые называют уровнями квантования. Если уровни квантования нумерованы, то результатом преобразования является число, которое может быть выражено в любой числовой системе. Округление с определенной разрядностью мгновенных значений непрерывной аналоговой величины с равномерным шагом по аргументу является простейшим случаем дискретизации и квантования сигналов при их преобразовании в цифровые сигналы.
Для производственных задач обработки данных обычно требуется значительно меньше информации, чем ее поступает от измерительных датчиков в виде непрерывного аналогового сигнала. При статистических флюктуациях измеряемых величин и конечной погрешности средств измерений информация о величине сигнала всегда ограничена. Рациональное выполнение дискретизации и квантования исходных данных дает возможность снизить затраты на хранение и обработку информации. Использование цифровых сигналов позволяет применять методы кодирования информации с возможностью последующего обнаружения и исправления ошибок при обращении информации. Цифровая форма сигналов облегчает также унификацию операций преобразования информации на всех этапах ее обращения.
Задачи дискретизации функций. Принципы дискретизации
Сущность дискретизации аналоговых сигналов заключается в том, что непрерывность во времени аналоговой функции s(t) заменяется последовательностью коротких импульсов, амплитудные значения которых cn определяются с помощью весовых функций, либо непосредственно выборками (отсчетами) мгновенных значений сигнала s(t) в моменты времени tn.Представление сигнала s(t) на интервале Т совокупностью дискретных значений cn записывается в виде:
(с1, с2, ... , cN) = А[s(t)],
где А - оператор дискретизации. Запись операции восстановления сигнала s(t):
s'(t) = В[(с1, с2, ... , cN)].
Выбор операторов А и В определяется требуемой точностью восстановления сигнала. Наиболее простыми являются линейные операторы. В общем случае:
с
n =где q
n(t) - система весовых функций.Отсчеты в выражении (5.1.1) связаны с операцией интегрирования, что обеспечивает высокую помехоустойчивость дискретизации. Однако в силу сложности технической реализации "взвешенного" интегрирования, последнее используется достаточно редко, при высоких уровнях помех. Более широкое распространение получили методы, при которых сигнал s(t) заменяется совокупностью его мгновенных значений s(t
n) в моменты времени tn. Роль весовых функций в этом случае выполняют гребневые (решетчатые) функции. Отрезок времени Dt между соседними отсчетами называют шагом дискретизации. Дискретизация называется равномерной с частотой F=1/Dt, если значение Dt постоянно по всему диапазону преобразования сигнала. При неравномерной дискретизации значение Dt между выборками может изменяться по определенной программе или в зависимости от изменения каких-либо параметров сигнала.Воспроизведение непрерывного сигнала
Воспроизведение непрерывного сигнала по выборкам может проводиться как на основе ортогональных, так и неортогональных базисных функций. Воспроизводящая функция s'(t) соответственно представляется аппроксимирующим полиномом:
s'(t) =![]() cn vn(t), (5.1.2)
cn vn(t), (5.1.2)
где v
n(t) - система базисных функций. Ортогональные базисные функции обеспечивают сходимость ряда к s(t) при n Ю Ґ . Оптимальными являются методы дискретизации, обеспечивающие минимальный числовой ряд при заданной погрешности воспроизведения сигнала. При неортогональных базисных функциях используются, в основном, степенные алгебраические полиномы вида: s'(t) =![]() cn tn. (5.1.3)
cn tn. (5.1.3)
Если значения аппроксимирующего полинома совпадают со значениями выборок в моменты их отсчета, то такой полином называют интерполирующим. В качестве интерполирующих полиномов обычно используются многочлены Лагранжа. Для реализации интерполирующих полиномов необходима задержка сигнала на интервал дискретизации, что в системах реального времени требует определенных технических решений. В качестве экстраполирующих полиномов используют, как правило, многочлены Тейлора.
Естественным требованием к выбору частоты дискретизации является внесение минимальных искажений в динамику изменения сигнальных функций. Логично полагать, что искажения информации будут тем меньше, чем выше частота дискретизации F. С другой стороны также очевидно, что чем больше значение F, тем большим количеством цифровых данных будут отображаться сигналы, и тем большее время будет затрачиваться на их обработку. В оптимальном варианте значение частоты дискретизации сигнала F должно быть необходимым и достаточным для обработки информационного сигнала с заданной точностью, т.е. обеспечивающим допустимую погрешность восстановления аналоговой формы сигнала (среднеквадратическую в целом по интервалу сигнала, либо по максимальным отклонениям от истинной формы в характерных информационных точках сигналов).
Равномерная дискретизация. Спектр дискретного сигнала
Допустим, что для обработки задается произвольный аналоговый сигнал s(t), имеющий конечный и достаточно компактный фурье-образ S(f). Равномерная дискретизация непрерывного сигнала s(t) с частотой F (шаг
Dt = 1/F) с математических позиций означает умножение функции s(t) на гребневую функцию ШDt(t) = sDt(t) = s(t)Ч ШDt(t) = s(t)![]() d(t-kDt) =
d(t-kDt) =![]() s(kDt)d(t-kDt). (5.2.1)
s(kDt)d(t-kDt). (5.2.1)
С учетом известного преобразования Фурье гребневой функции
Ш
Dt(t) Ы (1/T)фурье-образ дискретной функции s
Dt(t):SF(f) = S(f) * FЧ ШF(f). (5.2.3)
Отсюда, для спектра дискретного сигнала имеем:
SF(f) = FЧ S(f) *![]() d(f-nF) = F
d(f-nF) = F![]() S(f-nF). (5.2.4)
S(f-nF). (5.2.4)
Из выражения следует, что спектр дискретного сигнала представляет собой непрерывную периодическую функцию с периодом F, совпадающую (при определенных условиях конечности спектра непрерывного сигнала) с функцией F
Ч S(f) непрерывного сигнала s(t) в пределах центрального периода от -fN до fN, где fN = 1/2Dt = F/2. Частоту fN (или для круговой частоты wN = p/Dt) называют частотой Найквиста. Центральный период функции SF(f) называют главным частотным диапазоном.Интуитивно понятно, что если спектр главного частотного диапазона с точностью до постоянного множителя совпадает со спектром непрерывного сигнала, то по этому спектру может быть восстановлена не только форма дискретного сигнала, но и форма исходного непрерывного сигнала. При этом шаг дискретизации и соответствующее ему значение частоты Найквиста должны иметь определяющее значение.
Как правило, шаг дискретизации сигнала (шаг числовых массивов) условно принимают равным
Dt = 1, при этом главный частотный диапазон занимает интервал -0.5 Ј f Ј 0.5, или, в шкале угловых частот, соответственно -p Ј w Ј p.Физическая сущность формирования спектров дискретных сигналов достаточно проста. Наиболее наглядно это можно увидеть, если воспользоваться программой Mathcad (см. рис. 5.2.1).
Сначала представим себе непрерывный сигнал постоянной единичной амплитуды c(t) = const = 1 на произвольном интервале 0-Т, например, при Т=100. Начнем дискретизировать сигнал с равномерным шагом
Dt=1. Вычислим спектр первого дискретного отсчета c0 = 1. При N=1 сигнал является импульсом Кронекера, а, соответственно, модуль спектра отсчета с0=1 представляет собой непрерывное частотное распределение |С(w)| = const в диапазоне от -Ґ до +Ґ (показан только участок от -6p до +6p с нормировкой на N для наглядности сравнения спектров). Все частоты сигнала имеют нулевую фазу и при сложении взаимно компенсируются во всех временных точках за исключением точки t=0, в которой амплитуды частот суммируются, создавая единичный отсчет с0.Добавим к сигналу второй дискретный отсчет с
1=1 (N=2). Если вычислить спектр только второго отсчета, то его модуль будет равен модулю первого отсчета (так как с1=с0), но нулевые фазы гармоник этого спектра переместятся в точку t=1, т.е. относительно точки t=0 фазы гармоник второго отсчета изменятся на -wDt в соответствии с теоремой запаздывания преобразования Фурье. При сложении этих двух спектров первого и второго отсчета наблюдается интерференция частот и возникают пульсации частотного спектра с максимумами на частотах, кратных F=1/Dt или в угловых единицах 2p/Dt, где фазы спектров первого и второго отсчетов совпадают и равны нулю. Форма модуля результирующего спектра при N=2 приведена на рисунке.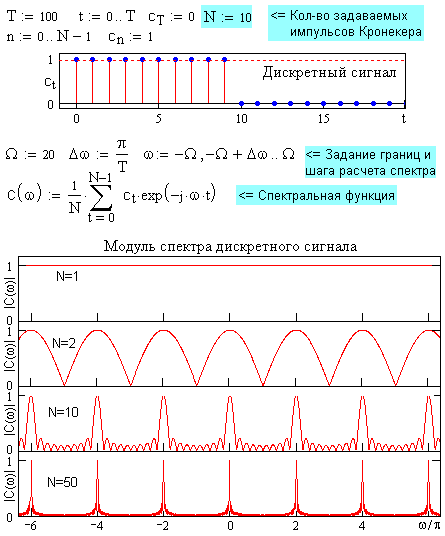
При дальнейшем увеличении количества отсчетов периодичность совпадения нулевых фаз и положения максимумов сохраняется, а интерференция частот между максимумами усложняется, при этом ширина главных пиков по всему частотному диапазону спектра от минус до плюс бесконечности становится все уже. На рис. 5.2.1 приведены примеры спектров сигналов при N=10 и N=50. В пределе, при двусторонней временной шкале ±Т
® ±Ґ и N® Ґ , гребневая функция из импульсов Кронекера во временной области ct ® ШDt(t) =Физический смысл интерференции частот остается тем же самым, если мы на произвольном интервале Т зададим произвольный сигнал, например – синусоиду u(t)
Ы U(f), и выполним его дискретизацию, т.е. умножим сигнал на непрерывную последовательность импульсов Кронекера c(t)Ч u(t) ® u(t)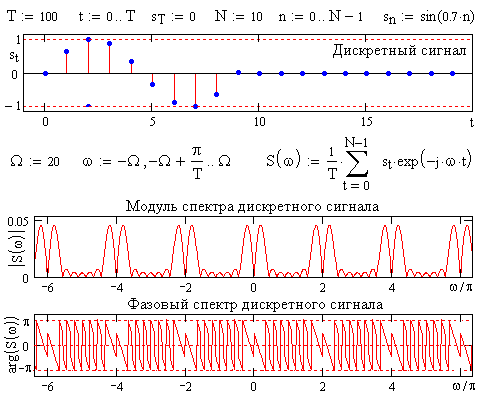
Математически произведение двух функций во временной области отображается сверткой спектров этих функций в частотном представлении, т.е. сверткой спектра сигнала u(t) с частотной гребневой функцией спектра, порожденной временной гребневой функцией дискретизации u(t)Ш
Dt(t) Ы U(f) * FЧ ШF(f), откуда и следует формула (5.2.4). Пример дискретизации одного периода синусоиды приведен на рис. 5.2.2.Вернемся к значению и роли частоты Найквиста при дискретизации сигналов.
На рис. 5.2.3 и 5.2.4. приведены примеры равномерной дискретизации аналоговых сигналов s
1(t) = exp(-a|t|) и s2(t) = exp(-bt2) (дискретные отсчеты нанесены кружками) и спектры этих дискретных сигналов.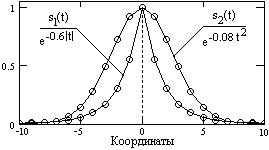
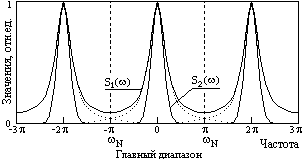
Рис. 5.2.3. Дискретные сигналы. Рис. 5.2.4. Спектры дискретных сигналов.
Для того чтобы периодическое повторение спектра, вызванное дискретизацией аналогового сигнала, не изменяло спектр в главном частотном диапазоне (по отношению к спектру исходного аналогового сигнала), необходимо и достаточно, чтобы максимальные частотные составляющие f
max в спектре аналогового сигнала не превышали частоты Найквиста (fmax Ј fN = F/2). Это означает, что частота дискретизации сигнала должна быть минимум в два раза выше максимальной частотной составляющей в спектре сигнала:F = 1/Dt і 2fmax, (5.2.5)
что обеспечивает выход спектра на нулевые значения на концах главного диапазона, как это имеет место для спектра S
2(w) на рис. 5.2.4.Другими словами, на одном периоде колебаний с частотой f
max должно быть минимум две точки отсчета. Это и понятно – по одной точке отсчета на периоде гармонического сигнала определение трех неизвестных параметров данной гармоники (амплитуда, частота, фаза) невозможно.Если условие (5.2.5) нарушается, искажения частотного спектра исходного аналогового сигнала неизбежны. На рис. 5.2.4 наглядно видно, что частота дискретизации для сигнала s
1(t) данному условию не удовлетворяет, спектры периодов перекрылись, и результирующий спектр дискретных отсчетов сигнала s1(t) отличается от фактического спектра сигнала s2(t) (фактический спектр и его периодические повторения в области перекрытия спектра главного частотного диапазона со спектрами боковых диапазонов показаны пунктиром).Характер возникающих искажений во временной области при нарушении условия (5.2.5) можно наглядно видеть на рис. 5.2.5. На рисунке показаны три возможных варианта соотношения частот гармонических сигналов с постоянной частотой их дискретизации.
1. График А – частота гармонического сигнала меньше частоты Найквиста. Дискретным отсчетам может соответствовать только исходная гармоника, амплитуда, частота и фаза которой могут быть однозначно определены по любым трем последовательным точкам (три уравнения, три неизвестных).
2. График В – частота гармонического сигнала равна частоте Найквиста. Это означает периодическое повторение каждой пары последовательных отсчетов, а, следовательно, для решения имеется только два уравнения с тремя неизвестными с возможностью определения только частоты, и то
при условии, что начальная фаза сигнала не совпадает с начальной фазой частоты дискретизации (в этом случае все отсчеты нулевые). Амплитуда и фаза сигнала определяются однозначно только при условии совпадения отсчетов с экстремумами гармоники.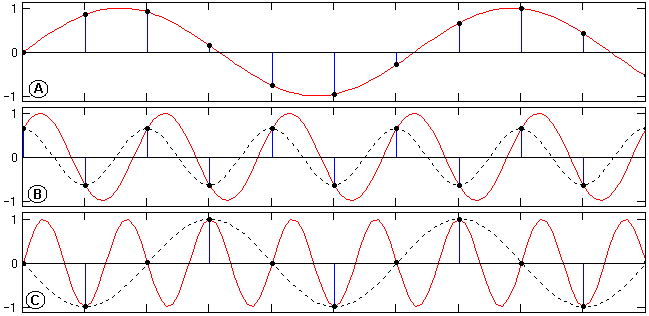
Рис. 5.2.5. Дискретизация гармоник с разной частотой.
3. График С – частота гармонического сигнала больше частоты Найквиста. Решение трех уравнений по трем последовательным точкам позволяет определить амплитуду гармоники, но дает искаженные значения частоты и фазы колебания (показано пунктиром). Это так называемый эффект появления ложных (кажущихся) частот
(aliasing). Частоты гармонических колебаний выше частоты Найквиста как бы зеркально "отражаются" в главный частотный диапазон от его границ (на частоте Найквиста), что можно видеть на рис. 5.2.4 для действительного спектра сигнала S1(w), показанного точками. Этот эффект аналогичен всем известному эффекту обратного вращения колес автомобиля (и любых других быстро вращающихся объектов) на экранах кино и телевизоров, когда скорость их вращения начинает превышать частоту смены кадров.Интерполяционный ряд Котельникова-Шеннона
Спектр дискретизированного сигнала (5.2.4) представляет собой сумму сдвинутых копий исходного аналогового сигнала с шагом сдвига, равным частоте дискретизации. Очевидно, что если спектры копий не перекрываются, то по центральной копии дискретного спектра можно восстановить исходный аналоговый сигнал с абсолютной точностью. Умножая функцию (5.2.3) на прямоугольную весовую функцию П
F(f), равную 1 в пределах главного частотного диапазона [-F/2,F/2] и нулю за его пределами, получаем непрерывный спектр в бесконечных по частоте границах, равный спектру FЧ S(f) в пределах главного частотного диапазона:FЧ S(f) = FЧ [S(f) * ШF(f)]Ч ПF(f). (5.2.6)
Обратное преобразование Фурье такого спектра должно давать конечный и непрерывный сигнал. Произведем обратное преобразование обеих частей равенства (5.2.6):
F·[S(f) * ШF(f)] Ы sDt(t), ПF(f) Ы FЧ sinc(pFt).
FЧ s(t) = sDt(t) * FЧ sinc(pFt).
s(t) = sinc(pFt) *![]() s(kDt)d(t-kDt),
s(kDt)d(t-kDt),
Дискретизированный сигнал s
Dt(t) =d
(t-kDt) * sinc(pFt) = sinc[pF(t-kDt)],выходной сигнал будет представлять собой сумму сдвинутых весовых импульсных откликов системы, где значение веса определяется отсчетами дискретного сигнала:
s(t) =![]() s(kDt) sinc[pF(t-kDt)] =
s(kDt) sinc[pF(t-kDt)] =![]() s(kDt) sinc[p(t/Dt-k)]. (5.2.7)
s(kDt) sinc[p(t/Dt-k)]. (5.2.7)
Эта конечная формула носит название интерполяционного ряда Котельникова-Шеннона. Из нее следует, что если наибольшая частота в спектре произвольной непрерывной функции s(t) не превышает частоты ее дискретизации, то она без потери точности может быть представлена в виде числовой последовательности дискретных значений s(k
Dt), k = 0,1,2,... , и однозначно восстановлена по этой последовательности. В этом и состоит сущность теоремы отсчетов Котельникова. В зарубежной литературе она называется также теоремой Шеннона или теоремой дискретизации (sampling teorem).Академик В.А.Котельников, 1908-2005.
Крупнейший ученый в области радиотехники, радиофизики и информатики. Окончил Московский энергетический институт в 1931 году. С 1931 г. по 1941 г. преподает в МЭИ и ведет научную работу в ЦНИИ связи. В 1933 г. формулирует знаменитую теорему отсчетов, которая носит его имя. В период Великой Отечественной войны (1941-1945 гг.) работал над созданием специальной аппаратуры связи. С 1948 г. по 1953 г. директор и главный конструктор ОКБ МЭИ. В 1953 году избран академиком АН СССР. С 1954 года - директор Института радиотехники и электроники АН СССР. Занимался теорией помехоустойчивой радиосвязи и радиолокации, радиолокационным исследованием планет. Лауреат Ленинской премии, дважды лауреат Государственной премии СССР. Дважды удостоен звания Героя Социалистического труда, награжден шестью орденами Ленина, орденом "За заслуги перед Отечеством" I степени.По существу, ряд (5.2.7) представляет собой частный случай разложения сигнала в соответствии с формулой (5.1.2) по системе ортогональных функций интегрального синуса v(t, k
Dt)= sinc(pF(t-kDt))= sinc(p(t/Dt – k)), образующих базис пространства сигналов s(t). Для проверки ортогональности достаточно вычислить скалярное произведение базисных функций:![]() v(t,nDt) v(t,mDt) dt =
v(t,nDt) v(t,mDt) dt = ![]() .
.
Разложение (5.2.7) проще и понятнее, чем разложение в ряды Фурье, что можно видеть на рис. 5.2.6. Вес каждой функции отсчетов sinc[
pF(t-kDt)] формирует пиковое значение интегрального синуса в каждой текущей точке t= kDt, равное значению сигнала s(kDt), при этом во всех остальных точках дискретных отсчетов sinc[pF(t-(k±j)Dt))], j= 1,2,… значения интегрального синуса равны нулю. Ряд числовых значений интегрального синуса для дискретных значений t= nDt при суммировании по k полностью эквивалентен гребневой функции:![]() sinc[pF(nDt-kDt)] є ШDt(t).
sinc[pF(nDt-kDt)] є ШDt(t).
Однако, в отличие от гребневой функции, в интервале между дискретными отсчетами интегральный синус имеет не нулевые, а определенные осциллирующие значения. Суперпозицией этих значений по текущим значениям t от всех интегральных синусов, осцилляции которых доходят до данного значения t, и образуются значения аналогового сигнала в интервалах между отсчетами.

Рис. 5.2.6. Восстановление непрерывного сигнала по дискретным отсчетам.
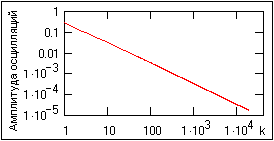
В принципе, функции отсчетов имеют бесконечные осцилляции, и восстанавливают аналоговый сигнал, бесконечный по аргументу. Амплитуда осцилляций функций отсчетов затухает достаточно медленно (см. рис. 5.2.7). Однако на рис. 5.2.6 нетрудно заметить, что, в силу знакопеременности функций отсчетов по интервалам дискретизации, осцилляции восстанавливаемых кривых с финитным спектром затухают достаточно быстро, и для данных без существенных выбросов и больших перепадов значений определяются, в основном, отсчетами, ближайшими к интерполируемому интервалу. Это позволяет ограничивать интервал суммирования в формуле (2.5.7) определенными окрестностями текущих точек интерполяции.
Курсовая работа 1 – Исследование и разработка основных правил ограничения интервала суммирования при интерполяции данных рядом Котельникова-Шеннона.
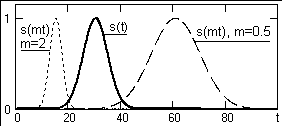
Ряд (5.2.7) позволяет простым введением масштабного множителя в аргумент интегрального синуса изменять представление сигнала на временной оси, растягивать или сжимать сигнал:
s(t) =![]() s(kDt) sinc[pF(m·t-kDt)].
s(kDt) sinc[pF(m·t-kDt)].
По аналогичной формуле может выполняться пересчет дискретных данных на другой интервал дискретизации:
s(n·Dtnew) = ![]() s(kDt) sinc[pF(n·Dtnew-kDt)].
s(kDt) sinc[pF(n·Dtnew-kDt)].
Примеры восстановления аналоговой форму произвольного финитного сигнала и изменения шага дискретизации данных приведены на рис. 5.2.9.
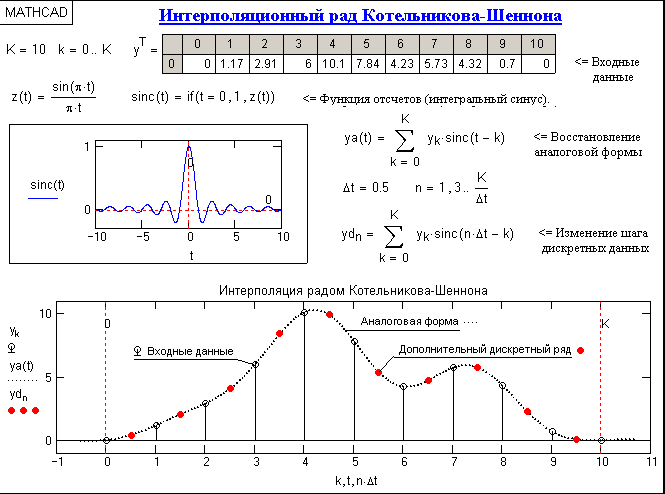
Рис. 5.2.9. Интерполяция по Котельникову-Шеннону.
На рис. 5.2.10 приведено моделирование дискретизации аналогового сигнала, влияние наложение спектров боковых периодов на спектр главного диапазона дискретного сигнала и восстановление из этого спектра аналоговой формы сигнала.
Графики А и Б рисунка – модельный аналоговый сигнал, точки его дискретизации и модуль спектра дискретного сигнала. Вычисление спектра выполнено быстрым преобразованием Фурье (БПФ) и отображает, соответственно, частотный диапазон 0-2f
N. Дискретизация выполнена корректно, с выполнением условия (5.2.5), о чем можно судить и по спектру дискретного сигнала (график Б, выход на незначимые значения к частоте Найквиста fN).Кривая S1 на графике В – спектр модельного дискретного сигнала при нарушении условия (5.2.5). В данном случае это произойдет при увеличении шага дискретизации в 2 раза, что вызовет уменьшение в 2 раза новой частоты Найквиста и перемещение границы главного диапазона на отметку 0.5f
N на графике Б, при этом произойдет перекрытие спектров поддиапазонов. На графике приведены кривые S1a и S1b, которые являются раздельными спектрами правой половины главного диапазона без сложения со спектром правого бокового диапазона (интервал 0-2fN, где fN – частота Найквиста новой дискретизации), и левой половины правого бокового диапазона на том же интервале 0-2fN без сложения со спектром главного диапазона. Хорошо видны “хвосты” спектров, выходящие за границы интервала Найквиста от центров диапазонов и заходящие в соседние диапазоны. Сложением этих спектров в интервале 0-2fN нетрудно убедиться, что полученный результат будет полностью соответствовать спектру S1 новой дискретизации исходного сигнала. Обратим внимание, что сложение спектров рядом расположенных диапазонов может вызывать не только увеличение высокочастотных составляющих (как это можно было видеть на рис. 5.2.4 – спектр S1), ни и их взаимную компенсацию, как имеет место для спектра S1 в данном случае (кривая точками на графике В).Перекрытие спектров диапазонов вызовет искажение аналоговой формы сигнала, восстановленного из его дискретных отсчетов, что можно видеть на графике Г – кривая s2. В данном случае, при частичной взаимной компенсации перекрывающихся частей спектров, наиболее сильное искажение произошло во второй, высокочастотной части сигнала.
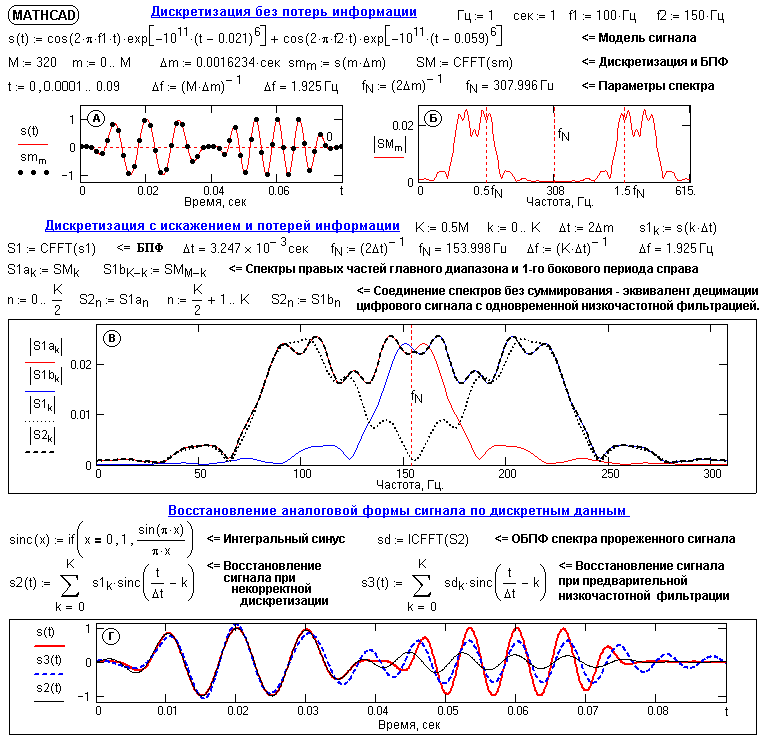
Рис. 5.2.10. Моделирование дискретизации аналогового сигнала.
Дискретизируемые сигналы, как правило, содержат широкополосные шумы, высокочастотные составляющие которых неизбежно перекрываются при периодизации спектра, и увеличивают погрешность восстановления сигналов. Для исключения этого фактора перед проведением дискретизации должно быть обеспечено подавление всех частот выше частоты Найквиста, т.е. выполнена низкочастотная фильтрация сигнала. Если последнее не проведено, то при дискретизации целесообразно в 2-4 раза уменьшить интервал дискретизации относительно оптимального и первой операцией обработки данных выполнить низкочастотную цифровую фильтрацию, после чего можно провести децимацию данных.
Увеличение интервала дискретизации сигналов является довольно распространенной операцией при цифровой обработке данных, и не только при подготовке данных для хранения с целью сокращения их количества. При комплексной обработке данных различной природы интервалы дискретизации этих данных могут оказаться различными, и производится их приведение к одному значению. Аналогичная операция выполняется, как правило, и при создании многослойных информационных пакетов. В таких случаях снижение частоты дискретизации каких-либо данных является вынужденной необходимостью даже с потерей части высокочастотных составляющих информации. Предварительное отфильтровывание отбрасываемых данных перед децимацией (для исключения их попадания в главный частотный диапазон и искажения основной информации) в этом случае является обязательным, особенно при достаточно высокой энергии этих составляющих сигнала. Пример такой децимации приведен на рис. 5.2.10 на графиках В и Г - спектр S2(f) децимированных данных и аналоговый сигнал s2(t), восстановленный по дискретным отсчетам sd(k
Dt) ↔ S2(f). Децимация выполнена непосредственно в частотной области путем смыкания на частотной части 0-fN спектра SM(f) исходного сигнала sm(mDm) с сопряженной частью на интервале 1.5fN- fN, что сокращает новый интервал Найквиста в 2 раза и формирует спектр S2(f), соответствующий дискретному сигналу с увеличенным в два раза интервалом дискретизации данных с полностью подавленной частью спектральных составляющих от 0.5fN до 1.5fN. Такой метод может применяться для децимации (передискретизации) данных с любой кратностью.Дискретизация с усреднением
Если дискретизация сигнала производится импульсами конечной ширины, то таким импульсам соответствуют средние значения сигнала на интервале длительности импульсов. При длительности импульсов r имеем:
s(kDt) = (1/r)![]() s(t) dt. (5.2.8)
s(t) dt. (5.2.8)
С использованием селектирующей и гребневой функций эта операция отображается следующим образом:
sDt(t) = (1/r)[s(t) * Пr(t)]ШDt(t). (5.2.9)
Соответственно спектр дискретной функции:
SF(f) = [S(f)Ч sinc(pfr)] * FЧ ШF(f). (5.2.10)
Отсюда следует, что при дискретизации с усреднением спектр S(f) заменяется спектром S(f)
Ч sinc(pfr), периодическое продолжение которого и образует спектр дискретной функции. При обратном преобразовании Фурье и при использовании интерполяционной формулы Котельникова-Шеннона, вместо исходной функции s(t) получаем функцию s'(t) = s(t) * Пr(t)/r, что эквивалентно пропусканию сигнала через фильтр с откликом h(t) = Пr(t)/r, т.е. через низкочастотный сглаживающий фильтр "скользящего" среднего с окном r.Допустим r=
lDt, lЈ 1, F=2afmax, aі 1. Для этих условий частотная передаточная функция фильтра записывается в следующем виде: H(f) = sinс[(pl/2a)(f/fmax)]. Если потеря составляющих сигнала на всех частотах не должна превышать 3%, необходимо выполнить условие: sinc(pl/2a)і 0,97. При a=1 отсюда следует, что значение l должно быть равно lЈ 0.27, т.е. ширина импульса дискретизации может составлять до 27 % интервала дискретизации.Отметим, что в выражении (5.2.8) значения отсчетов относится к центру интервалов r импульсов дискретизации. Если отсчет будет относиться к концу интервалов r, что имеет место при обработке информации в режиме реального времени, то в выходной функции (5.2.9) появится сдвиг на интервал r/2, а в ее спектре соответственно сдвиг фаз на
wr/2 (в правой части выражения (5.2.10) добавится множитель exp(-jpfr)).Дискретизация спектров
Теоремы, доказанные для прямого преобразования Фурье, в такой же мере действительны и для обратного. При дискретизации спектра сигнала с шагом Df динамическое представление сигнала также становится периодическим с периодом Т = 1/Df. Для сохранения возможности точного восстановления сигнала в пределах главного периода (без наложения сигналов соседних периодов) частотный шаг дискретизации должен удовлетворять условию:
D
f Ј 1/T. (5.2.11)Попутно отметим, что для временной формы каузального сигнала главным периодом принимают интервал от 0 до Т, хотя при обработке данных на ЭВМ это не имеет значения и главный период может устанавливаться от -Т/2 до Т/2.
Информационная тождественность динамической и частотной форм дискретного представления сигнала непосредственно следует из теоремы Котельникова-Шеннона.
Основой любых преобразований при обработке данных обычно является финитный (конечный по длительности) сигнал, зарегистрированный на интервале 0-Т и состоящий из определенных частотных составляющих от 0 до f
max. Оптимальная дискретизация аналогового сигнала без потери точности его восстановления, как рассмотрено выше, соответствует двум отсчетам на периоде максимальной частотной составляющей:D
t = 1/2fmax, Nt = T/Dt. (5.2.12)где N
t – общее количество отсчетов на интервале Т задания сигнала. Если сигнал зарегистрирован непосредственно в дискретной форме, то он автоматически ограничен по максимальной частоте, т.е. максимальные частоты в таком сигнале равны fmax Ј 1/2Dt.При переводе дискретного сигнала в частотную форму спектр сигнала непрерывен и периодичен с периодом 1/
Dt = 2fN. Для оптимальной дискретизации по частоте без потери точности восстановления непрерывного спектра должны выполняться условия:D
f = 1/T = 1/(DtNt), fN = 1/2Dt, (5.2.13)Nf = 2fN/Df = Nt. (5.2.14)
Спектр сигнала подвергается каким-либо преобразованиям (обработке), как правило, только в главном частотном диапазоне и тем самым превращается в непериодический сигнал, существующий только в интервале 2f
N (от -fN до fN). Значения спектра за пределами главного диапазона по умолчанию полагаются равными нулю. При обратном переводе такого сигнала из частотной формы в динамическую сигнал также является непрерывным и периодическим с периодом 1/Df = T, при этом оптимальная дискретизация по координатам без потери точности восстановления непрерывной формы соответствует условиям:D
t = 1/2fN, T = 1/Df, (5.2.15)Nt = T/Dt = Nf. (5.2.16)
При осуществлении преобразований s(k
Dt) Ы S(nDf), равно как и S(nDf) Ы s(kDt), условие Nf = Nt является необходимым и достаточным для полного сохранения информации при преобразованиях сигнала из одной формы представления в другую. Условия (5.2.12-5.2.16) задают оптимальность преобразований без потерь информации. Если исходный сигнал дискретизирован оптимально и представлен N отсчетами, то уменьшение количества отсчетов при преобразовании неизбежно приводит к определенным потерям информации.
Что касается увеличения числа отсчетов при преобразовании функций (уменьшение интервалов дискретизации), то оно всегда возможно, т.к. выходной сигнал преобразования финитных сигналов является непрерывной функцией и, в принципе, интервал дискретизации может быть установлен бесконечно малым. Однако увеличение числа отсчетов не увеличивает ни количества информации, заключенной в исходном сигнале, ни точности ее представления.
По существу, такая операция полностью эквивалентна интерполяции исходного сигнала рядом Котельникова-Шеннона. Пример такой операции приведен на рис. 5.2.11.Отсчеты s(k
Dt) и огибающая их кривая на рисунке 5.2.11 повторяют (в более детальном масштабе) сигнал s1(t) на рис. 5.2.3, дискретизированный с шагом Dt = 1. Как уже отмечалось, интервал дискретизации данного сигнала оказался завышенным, и спектр сигнала искажен (рис. 5.2.4). При выполнении операции s(kDt) Ю S(nDf) количество точек дискретизации спектра S(nDf) было увеличено в 5 раз по отношению к количеству точек сигнала s(kDt), т.е. Nf = 5Nt. При обратном преобразовании S(nDf) Ю z(kDt), были выполнены условия (5.2.15-5.2.16), при этом шаг дискретизации сигнала при его восстановлении оказался также в 5 раз меньше исходного (Dt = 0.2). Результат можно видеть на рис. 5.2.11 (кривая z(kDt)). Абсолютно такой же результат дает и интерполяция сигнала s(kDt) рядом Котельникова-Шеннона с переводом на шаг Dt = 0.2. Искажение аналогового сигнала закладывается при его дискретизации, если шаг дискретизации не удовлетворяет условию (5.2.5), и при любых дальнейших преобразованиях уже не может быть исправлено, т.к. информация о первоначальной форме аналогового сигнала при некорректной дискретизации утрачивается безвозвратно.Дискретизация усеченных сигналов
При выполнении условия (5.2.5) для сигналов с ограниченным спектром аналоговая форма сигнала может быть восстановлена по дискретным отсчетам, если сигнал на интервале Т его задания является финитным или, по крайней мере, настолько быстро затухающим, что отсчеты сигнала за пределами интервала Т практически равны нулю. Задача дискретизации усложняется для медленно затухающих сигналов, сигналов бесконечной длительности и сигналов со спектром, неограниченным по частоте. Последнее имеет место, если в сигнале присутствуют разрывы и резкие скачки.
В общем случае, длительность сигнала и ширина его спектра не могут быть одновременно ограничены конечными интервалами. Если длительность сигнала ограничена и сигнал урезан в области не нулевых значений, то спектр сигнала неограничен и наоборот. Однако обработка реальных сигналов возможна только с их ограничением, как по координатам, так и по ширине спектра. При этом в качестве оценки корректности ограничения сигналов используется энергетический критерий, согласно которому длительность сигнала Т и практическую ширину спектра
W устанавливают такими, чтобы в них была сосредоточена подавляющая часть энергии сигнала. Это достигается при выполнении условий:![]() |s(t)|2 dt = k
|s(t)|2 dt = k![]() |s(t)|2 dt, (5.2.17)
|s(t)|2 dt, (5.2.17)
![]() |S(w)|2 dw = k
|S(w)|2 dw = k![]() |S(w)|2 dw, (5.2.17')
|S(w)|2 dw, (5.2.17')
где k- коэффициент представительности (качества) задания сигнала, значение которого, в зависимости от целевых задач обработки сигналов, может устанавливаться от 0,9 до 0,99.
Допустим, что произвольный сигнал s(t) рассматривается в пределах конечного интервала [0, Т] и принимается равным нулю за его пределами. Такой сигнал может быть получен умножением сигнала s(t) на прямоугольную весовую функцию П
T(t):sT(t) = s(t) ПT(t).
Для спектра S
T(f) функции sT(f) соответственно имеем:ST(f) = S(f) * ТЧ sinc(pfT). (5.2.18)
Спектр
ST(f) неограничен, поскольку неограничен носитель функции sinc(pfT). Отсюда следует, что частота дискретизации функции sT(t) в принципе должна быть бесконечно большой, т.е. корректная дискретизация невозможна. На практике полагают, что спектр ST(f) также определен в конечной области [-W,W]:S'T(f) = ST(f)Ч П2W(f),
при этом вне этой области, по оценке Шеннона, для спектра S
T(f) справедлива формула:|ST(f)| » 1/WТ, f П (-W,W). (5.2.19)
Но усеченная часть спектра определяет разность значений между исходной функцией sТ(t) и функцией s'Т(t), восстановленной по усеченному спектру S'
T(f), т.к. отсеченных гармоник спектра будет недоставать для полного восстановления функции sT(f):e
T(t) = sT(t) – s'T(t).Соответственно, оценка дисперсии погрешности аппроксимации определяется выражением:
s2
=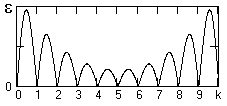
Эти выражения определяют порядок среднеквадратической погрешности аппроксимации, которая является интегральной по интервалу Т, а не локальной разностью значений s
T(t)–s'T(t). Типичный вид погрешности аппроксимации усеченных сигналов приведен на рис. 5.2.12. В точках дискретизации погрешность равна нулю, максимальна на центрах интервалов дискретизации и нарастает при приближении к границам интервала Т.Физические данные обычно регистрируются по определенным интервалам Т и, как правило, не выходят на нулевые значения на границах интервалов. В этом случае ограничение ширины спектра можно проводить по (5.2.20) с учетом допустимой среднеквадратической погрешности аппроксимации данных. Частота
W при усечении спектра может рассматриваться в качестве частоты Найквиста для сигнала sT(t) при его дискретизации, что определяет частоту дискретизации не менее F = 2W и количество точек дискретизации не менее N=TF=2WT.В силу тождественности свойств прямого и обратного преобразования Фурье аналогичная методика может применяться и для оценки условий дискретизации спектров.
Таким образом, дискретизация усеченных сигналов возможна, однако при обработке усеченных сигналов необходимо проявлять осторожность и контролировать как значение среднеквадратической ошибки искажений, так и характер возникающих искажений сигнала и его спектра. Так, например, при усечении функции автокорреляции в спектре мощности сигнала могут появиться отрицательные значения, т.к. функция отсчетов sinc(
pfT) в (5.2.18) является знакопеременной. Другой пример - проектирование частотных полосовых фильтров. При задании передаточной функции фильтра H(f) в частотной области в виде П-образной функции H(f) = Пr(f) обратное преобразование Фурье дает импульсный отклик фильтра h(t) Ы H(f) бесконечно большой длины. Усечение отклика hT(t) = h(t)ПT(t) вызывает изменение передаточной функции фильтра (явление Гиббса): HT(f) = Пr(f) * ПT(f) Ю Пr(f)Ч ТЧ sinc(pfT), при этом по краям скачков П-функции появляются затухающие флюктуации с амплитудой первого выброса до 9% от значений коэффициента передачи фильтра в полосе пропускания.Так как частотный характер искажений, возникающих при усечении сигнала, определяется весовой функцией П
T(t) Ы ТЧ sinc(pfT), то допустимый уровень и форму искажения сигнала можно устанавливать не только подбором интервала Т, но и применением других весовых функций. Так, для исключения появления отрицательных значений в спектрах мощности усечение функций автокорреляции целесообразно выполнять весовыми функциями, которые не имеют отрицательных значений в своих спектрах. Одной из таких функций является, например, треугольная весовая функция (окно Бартлетта).Соотношение спектров одиночного и периодического сигналов
Спектр S
T(f) = S(kDf) периодического сигнала sT(t) с периодом Т дискретен (Df = 1/T). Спектр S(f) одиночного сигнала s(t), заданного на интервале Т, непрерывен и представляет собой спектральную плотность сигнала при T Ю Ґ . Но периодический сигнал можно представить и в виде свертки одного периода с гребневой функцией Дирака:sT(t) = s(t) * ШT(t).
При переходе в частотную область получаем
:ST(f) = (1/T)Ч S(f)Ч Ш1/T(f) = S(kDf),
ST(f) = (1/T)![]() S(f)d(f-k/T). (5.2.21)
S(f)d(f-k/T). (5.2.21)
Отсюда следует, что спектр периодического сигнала представляет собой дискретизированный спектр одиночного сигнала, нормированный на длительность периода.
С другой стороны, одиночный сигнал s(t) может быть получен из периодического сигнала s
T(t) умножением на селектирующий прямоугольный импульс ПT(t):s(t) = sT(t)Ч ПT(t).
Спектр одиночного сигнала:
S(f) = TЧ ST(f) * ПT(f) = Т![]() S(kDf)Ч sinc[pT(f-k/T)], (5.2.22)
S(kDf)Ч sinc[pT(f-k/T)], (5.2.22)
т.е. непрерывный спектр одиночного сигнала однозначно устанавливается по спектру периодического сигнала (интерполяция рядом Котельникова-Шеннона в частотной области).
Дискретизация по критерию наибольшего отклонения
Задача абсолютно точного восстановления сигнала на практике обычно не ставится, в отличие от задачи минимального физического объема информации, при котором сохраняется возможность ее восстановления в непрерывной форме с определенным допустимым значением погрешности. Такая задача актуальна всегда, и особенно при дистанционных методах регистрации и обработки информации, передаче сигналов по каналам связи и при подготовке информации к
длительному хранению. Одним из методов решения этой задачи является дискретизация сигналов по критерию наибольшего отклонения.В процессе дискретизации по критерию наибольшего отклонения задается допустимое значение погрешности восстановления сигнала
s. При восстановлении сигнала непрерывная функция s(t) аппроксимируется, как правило, степенными полиномами n-го порядка. Погрешность восстановления функции s(t) полиномом sa(t) определяется остаточным членом L(t):L(t) = s(t) - sa(t) = s(t).
Шаг дискретизации выбирается из условия обеспечения L(t) <
s по всему интервалу определения функции s(t). Как правило, динамика функции s(t) может существенно изменяться в различные моменты времени по интервалу регистрации, при этом шаг дискретизации также может изменяться, при условии не превышения заданной погрешности на каждом шаге. При установленном значении s уменьшение числа отсчетов обеспечивается повышением степени аппроксимирующего многочлена. На практике обычно ограничиваются ступенчатой, линейной и параболической аппроксимацией полиномами соответственно нулевой, первой и второй степеней.В качестве интерполирующих многочленов используют многочлены Лагранжа. Для многочленов Лагранжа нулевой степени значение s
a(t) в момент времени t на интервале ti<t<ti+1 между двумя последовательными отсчетами функции принимается равным отсчету s(ti+1). Если восстановление сигнала s(t) проводить по двум отсчетам: sa(ti) = [s(ti+1)-s(ti)]/2, то при том же шаге дискретизации погрешность восстановления сигнала уменьшается вдвое. Но при использовании двух последовательных отсчетов лучше использовать многочлены Лагранжа первой степени, т.е. соединение двух последовательных отсчетов прямой линией, что дает еще большее уменьшение погрешности восстановления аналоговой формы сигнала.В качестве экстраполирующих многочленов используется многочлены Тейлора. Для многочлена Тейлора нулевой степени условия восстановления сигнала практически не отличаются от многочлена Лагранжа, за исключением направления (от текущего зарегистрированного отсчета и вперед по t). Для многочленов Тейлора более высоких степеней при восстановлении сигнала помимо отсчета s(t
i) используется также соответствующие значения производных в точке отсчета. Восстановление сигнала многочленами Тейлора происходит без задержки во времени. Однако при использовании многочленов выше нулевой степени для точного восстановления сигнала по сравнению с интерполяционными методами требуется в два раза более высокая частота дискретизации.Адаптивная дискретизация
Частота равномерной дискретизации информации рассчитывается по предельным значениям частотных характеристик сигналов. Адаптивная дискретизация ориентирована на динамические характеристики сигнала, что позволяет обеспечивать его восстановление при минимальном числе выборок. В основе принципов адаптивной дискретизации лежит слежение за текущей погрешностью восстановления сигнала. Наиболее широкое применение получили алгоритмы дискретизации с адаптацией по длине интервала аппроксимации. Сущность дискретизации заключается в последовательном наращивании интервала аппроксимации с непрерывным сравнением сигнала s(t) с воспроизводящей функцией s
a(t). При достижении заданного значения s наращивание интервала прекращается, и производится отсчет значения s(ti), т.е. дискретизация является неравномерной. Для воспроизведения сигналов нерегулярной дискретизации обычно используются степенные алгебраические полиномы нулевой и первой степени в интерполяционном или в экстраполяционном вариантах.Наиболее простой является техника адаптивной дискретизации с использованием многочлена нулевой степени. На момент t
i начала каждого интервала аппроксимирующий полином sa(t) принимается равным s(ti), вычисляется текущая разность L(t) = s(t)-sa(t) и производится сравнение ее значения с заданным значением s. При фиксировании равенства L(t) = s производится очередной отсчет и начинается следующий интервал.При использовании аппроксимирующего многочлена первой степени вычисляется значение s
a(t) = s(ti)+s'(ti), где s'(t) - производная сигнала. Момент очередного отсчета определяется выполнением равенства s(t)-s(ti)-s'(ti) = s . Следует иметь в виду, что данный алгоритм неэффективен при наличии высокочастотных помех, к которым весьма чувствительна операция дифференцирования.Курсовая работа 2 – Исследовать и разработать программу оценки спектра дискретного сигнала при неравномерном шаге дискретизации.
Самыми простыми способами восстановления сигналов при адаптивной дискретизации являются линейная и квадратичная интерполяции, которые выполняются по уравнениям:
f(x)лин = а0 + а1х. f(x)кв = а0 + а1х + а2х2.
Эти уравнения являются частным случаем полиномиальной интерполяции с помощью аппроксимирующего полинома:
f(x) = а0 + а1х + а2х2 + … + anxn =![]() ai·xi. (5.4.1)
ai·xi. (5.4.1)
Для выполнения полиномиальной интерполяции достаточно по выражению (5.4.1) составить систему линейных уравнений для n последовательных отсчетов и определить n значений коэффициентов a
i. При глобальной интерполяции, по всем N точкам задания функции, степень полинома равна N-1. Глобальная интерполяция обычно выполняется для достаточно коротких (не более 8-10 отсчетов) массивов данных. Пример выполнения глобальной интерполяции приведен на рис. 5.4.1.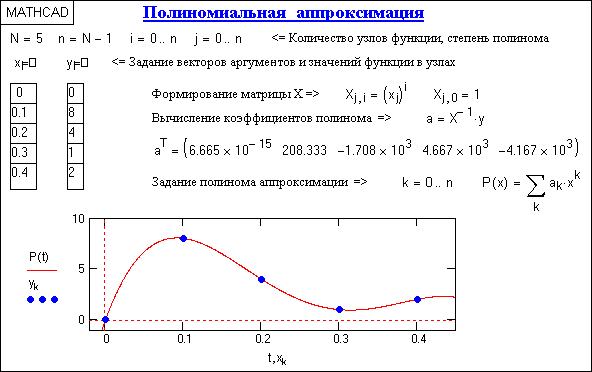
Рис. 5.4.1. Интерполяция данных.
Большие массивы данных интерполируются последовательными локальными частями или в скользящем по массиву данных окне интерполяции, как правило, с нечетным значением N и вычислением требуемых значений сигнала в определенном интервале центральной части окна.
Курсовая работа 3 – Исследовать и обосновать оптимальный метод полиномиальной интерполяции произвольных данных с равномерным шагом дискретизации. Разработать программу интерполяции.
Курсовая работа 4 – Исследовать и обосновать оптимальный метод полиномиальной интерполяции произвольных данных с неравномерным шагом дискретизации. Разработать программу интерполяции.
Для практического использования более удобны формулы аппроксимации, не требующие предварительного определения коэффициентов аппроксимирующих полиномов. К числу таких формул относится интерполяционных многочлен по Лагранжу /30/. При аппроксимации функции у(х) многочленом n-ой степени f(x):
f(x) = ![]() +
+ ![]() +…
+…
…+ ![]() . (5.4.2)
. (5.4.2)
Пример интерполяции по Лагранжу приведен на рис. 5.4.2.

Рис. 1.2.2. Интерполяция по Лагранжу.
Курсовая работа 5 – Исследовать и обосновать оптимальный метод интерполяции по Лагранжу произвольных данных с неравномерным шагом дискретизации. Разработать программу интерполяции.
Квантование сигналов
Дискретизация аналоговых сигналов с преобразованием в цифровую форму связана с квантованием сигналов. Сущность квантования состоит в замене несчетного множества возможных значений функции, в общем случае случайных, конечным множеством цифровых отсчетов, и выполняется округлением мгновенных значений входной функции s(ti) в моменты времени ti до ближайших значений si(ti) = niDs, где Ds- шаг квантования шкалы цифровых отсчетов. Квантование с постоянным шагом Ds называется равномерным. Математически операция квантования может быть выражена формулой:
si(ti) = ![]() ,
,
где скобки [..] означают целую часть значения в скобках.
При квантовании сигналов в большом динамическом диапазоне значений шаг квантования может быть и неравномерным, например, логарифмическим, т.е. пропорциональным логарифму значений входного сигнала. Установленный диапазон шкалы квантования от s
min до smax и шаг квантования Ds определяют число делений шкалы Ns = (smax-smin)/Ds и соответственно цифровую разрядность квантования. В результате дискретизации и квантования непрерывная функция s(t) заменяется числовой последовательностью {s(kDt)}. Погрешность округления ei = s(kDt)-si(kDt) заключена в пределах -Ds/2<e <Ds/2 и называется шумом квантования. Требуемая точность квантования оценивается по влиянию возникающего шума квантования на последующую обработку сигналов.При достаточно малом шаге квантования любое значение в его пределах можно считать равновероятным, при этом значения
e распределены по равномерному закону:p(e) = 1/Ds, -Ds/2 Ј e Ј Ds/2.
Соответственно, дисперсия и среднее квадратическое значение шума квантования:
e
2 = Ds2/12,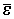 » 0.3 Ds. (5.5.1)
» 0.3 Ds. (5.5.1)
При задании уровня шума квантования с использованием выражения (5.5.1) нетрудно определить допустимое значение шага квантования.
Входной сигнал содержит, как правило, аддитивную смесь собственно сигнала s(t) и помехи q(t) с дисперсией соответственно
sq2. Если помехи не коррелированны с сигналом, то после квантования суммарная дисперсия шумов:s
2 = sq2+e2.На практике шаг квантования выбирают обычно таким, чтобы не происходило заметного изменения отношения сигнал/шум, т.е.
e2<<sq2.Децимация и интерполяция данных
Децимацией (прореживанием, сокращением) цифровых данных принято называть уплотнение данных с удалением избыточной информации. Последнее имеет место, если шаг дискретизации данных был установлен излишне подробным и fN = 1/2Dt >> fmax сигнала. Информация высокочастотной части сигнала может быть ненужной, если основная энергия полезной части сигнала заключена в низкочастотной области. Децимация может потребоваться и в том случае, если массивы данных представлены с разным шагом дискретизации.
Децимации должна предшествовать низкочастотная фильтрация данных. Это связано с тем, что в процессе децимации шаг дискретизации Dt заменяется на новый шаг Dt' = pDt, где p>1, с соответствующим сжатием главного частотного диапазона, при этом появляется опасность отражения отбрасываемых частотных составляющих и высокочастотных шумов в главный диапазон (как и при неправильном выборе шага дискретизации). Точка отсечки низкочастотного фильтра устанавливается по новой частоте Найквиста: fN'=1/(2pDt).
Значение коэффициента р при децимации может быть произвольным, но, как правило, используются целочисленные значения, и децимация выливается в простое прореживание данных. При нецелочисленном значении р децимация может проводиться с использованием интерполяционного ряда Котельникова-Шеннона (равно как и любого другого интерполяционного многочлена) или преобразования Фурье. Последнее выполняется путем перевода сигнала в частотную форму и возвращением в координатную форму с новым шагом
Dt' = pDt, при этом низкочастотная фильтрация может производиться непосредственно в частотном диапазоне. Возможно также и прямое усечение главного частотного диапазона с N точек до N' = N/p с возвратом из нового частотного диапазона в координатную форму с количеством точек N', но при этом следует учитывать последствия усечения спектральной функции (умножения на прямоугольное селектирующее окно) на форму восстанавливаемого по ней сигнала (свертка исходного сигнала с фурье-образом прямоугольного селектирующего окна).Интерполяция данных отличается от децимации только значением коэффициента р<1, с соответствующим увеличением частоты Найквиста, и не требует низкочастотной фильтрации.
Для децимации и интерполяции данных разработаны также специальные высокоскоростные методы и алгоритмы (цифровые фильтры) - экспандеры и компрессоры /4,5/.
Литература
4. Гольденберг Л.М. и др. Цифровая обработка сигналов: Справочник. - М.: Радио и связь, 1985.
5. Гольденберг Л.М. и др. Цифровая обработка сигналов: Учебное пособие для вузов.- М.: Радио и связь, 1990.- 256 с.
10. Дмитриев В.И. Прикладная теория информации: Учебник для вузов. - М.: Высшая школа, 1989.
16. Макс Ж. Методы и техника обработки сигналов при физических измерениях. - М.: Мир, 1983.
17. Никитин А.А. Теоретические основы обработки геофизической информации: Учебник для вузов.- М.: Недра, 1986.- 342 с.
21
. Рапопорт М.Б. Вычислительная техника в полевой геофизике: Учебник для вузов.- М.: Недра, 1993. - 350 с.30. Корн Г., Корн Е. Справочник по математике для научных работников и инженеров. – М.: Наука, 1984.
Copyright ©2006 Davydov А.V.
Реально идет речь о том, что релятивистские формулы не соответствуют астрономическим наблюдениям, давая на порядок и более меньшую массу и меньшую энергию. Отсюда сделан фокуснический вывод, что есть "темная материя" и "темная энергия", но не вывод, что релятивистские формулы не соответствуют реалиям. Подробнее читайте в FAQ по эфирной физике.
|
|
