ПРЕОБРАЗОВАНИЕ СИГНАЛОВ В СИСТЕМАХ
Введение.
4.1. Понятие систем. Линейные системы. Основные системные операции. Инвариантность систем к сдвигу. Математическая модель системы. Нерекурсивные системы. Рекурсивные системы.
4.2. Нерекурсивная фильтрация сигналов. Частотные характеристики фильтров. Расчет операторов нерекурсивных фильтров.
Литература.
введение
Преобразование и обработка сигналов осуществляется в системах. Понятия сигнала и системы неразрывны, так как любой сигнал существует в какой-либо системе его обращения. Система обработки сигналов может быть реализована как в материальной форме (специальное устройство, измерительный прибор и т.п.), так и программно на ЭВМ или на любом другом вычислительном устройстве. Существуют и комплексные измерительно-вычислительные системы (ИВС), которые выполняют как регистрацию и первичную обработку сигналов непосредственно в материальной форме их представления, так и преобразование сигналов в цифровую форму, и последующую программную обработку. Форма реализации систем существенного значения не имеет.
4.1. понятие систем [1, 25]
Система любого назначения всегда имеет вход, на который подается входной сигнал или входное воздействие, в общем случае многомерное, и выход, с которого снимается обработанный выходной сигнал. Если устройство системы и внутренние операции преобразований принципиального значения не имеют, то система в целом может восприниматься как “черный ящик”, в формализованном виде. Формализованная система представляет собой определенный системный оператор (алгоритм) преобразования входного сигнала – воздействия s(t), в сигнал на выходе системы y(t) – отклик или выходную реакцию системы. Символическое обозначение операции преобразования (трансформации):
y(t) = T[s(t)].
Системный оператор
T - это правило (набор правил, алгоритм) преобразования сигнала s(t) в сигнал y(t). Для общеизвестных операций преобразования сигналов применяются также расширенные символы операторов трансформации, где вторым символом и специальными индексами обозначается конкретный вид операции (как, например, TF - преобразование Фурье, TF-1 - обратное преобразование Фурье).Входной сигнал системы может представлять собой m - мерный вектор, а выходной сигнал n - мерный вектор, при этом система будет иметь m входов и n выходов. Пример такой системы в геофизике: трехканальный гамма-спектрометр. На три входа решающего блока спектрометра поступают потоки сигналов от калиевого, радиевого и ториевого каналов амплитудного анализатора спектрометра, а на три выхода решающего блока подаются результаты количественной интерпретации входной информации - сигналы количественных содержаний калия, урана и тория в точке измерений. Системный оператор спектрометра реализует алгоритм решения системы трех линейных уравнений с тремя неизвестными.
Для детерминированных входных сигналов соотношение между выходными и входными сигналами однозначно задается системным оператором. В случае реализации на входе системы случайного входного процесса также существует однозначное соответствие процессов на выходе и входе системы, однако при этом одновременно происходит изменение статистических характеристик выходного сигнала (математического ожидания, дисперсии, корреляционной функции и пр.), которое также определяется системным оператором.
Для полного определения системы необходимо задание характера, типа и области допустимых величин входных и выходных сигналов. Как правило, системы выполняются на сигналы одного типа по входу и выходу. По типу обработки входных сигналов они обычно подразделяются
на системы непрерывного времени, в основном для аналоговых или дискретных сигналов непосредственно в процессе измерений, и цифровые системы для обработки данных, зарегистрированных на промежуточных носителях. Совокупность системного оператора Т и областей входных/выходных сигналов образует математическую модель системы.Линейные системы.
Любые преобразования сигналов сопровождаются изменением их спектра и по характеру этих изменений разделяются на два вида: линейные и нелинейные. К нелинейным относят изменения, при которых в составе спектра сигналов появляются новые гармонические составляющие. При линейных изменениях сигналов изменяются амплитуды и/или начальные фазы гармонических составляющих спектра. Оба вида изменений могут происходить как с сохранением полезной информации, так и с ее искажением. Это зависит не только от характера изменения спектра сигналов, но и от спектрального состава самой полезной информации.Линейные системы
составляют основной класс систем обработки сигналов. Термин линейности означает, что система преобразования сигналов должна иметь произвольную, но в обязательном порядке линейную связь между входным сигналом (возбуждением) и выходным сигналом (откликом). В нелинейных системах связь между входным и выходным сигналом определяется произвольным нелинейным законом.Система считается линейной, если в пределах установленной области входных и выходных сигналов ее реакция на входные сигналы аддитивна (выполняется принцип суперпозиции сигналов) и однородна (выполняется принцип пропорционального подобия).
Принцип аддитивности
требует, чтобы реакция на сумму двух входных сигналов была равна сумме реакций на каждый сигнал в отдельности:T[a(t)+b(t)] = T[a(t)]+T[b(t)].
Принцип однородности
или пропорционального подобия требует сохранения однозначности масштаба преобразования при любой амплитуде входного сигнала:T[c ґ a(t)]= c ґ T[a(t)].
Другими словами, отклик линейной системы на взвешенную сумму входных сигналов должен быть равен взвешенной сумме откликов на отдельные входные сигналы независимо от их количества и для любых весовых коэффициентов, в том числе комплексных.
Примеры.
1. Система y(t) = a2t. y(t1) = a2t1, y(t2) = a2t2, y(ct) = a2ct.
y(t1+t2) = a2(t1+t2) = a2t1+a2t2 = y(t1)+y(t2). Система аддитивна.
cy(t) = ca2t = a2
ct = y(сt). Система однородна. И в целом линейна.2. Система y(t) = at
2. y(t1) = at12, y(t2) = at22, y(ct) = a(ct)2 = ac2t2.y(t1+t2) = a(t1+t2)2 № y(t1)+y(t2)= at12+at22. Система не аддитивна.
с y(t) = с at2 № y(сt) = ac2t2. Система неоднородна. И в целом нелинейна.
При программной реализации линейных систем на ЭВМ особых затруднений с обеспечением линейности в разумных пределах значений входных и выходных сигналов, как правило, не возникает. При физической (аппаратной) реализации систем обработки данных диапазон входных и/или выходных сигналов, в котором обеспечивается линейность преобразования сигналов, всегда ограничен и должен быть специально оговорен в технической документации или методической инструкции.
Основные системные операции.
К базовым линейным операциям, из которых могут быть сформированы любые линейные операторы преобразования, относятся операции скалярного умножения, сдвига и сложения сигналов: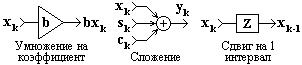
y(t) = b ґ x(t),
y(t) = x(t-Dt),
y(t) = a(t)+b(t).
Графическое отображение операций (цифровая форма) приведено на рис. 4.1.1.
Отметим, что операции сложения и умножения являются линейными только для аналоговых и дискретных сигналов. В случае цифровых сигналов они линейны относительно самих цифровых сигналов, но если последние - результат операции амплитудно-цифрового преобразования, то сложение и умножение не может считаться линейным абсолютно точно по отношению к исходным сигналам.
Для систем, с размерностью 2 и более существует также еще одна базовая операция, которая называется операцией пространственного маскирования, которая может рассматриваться как обобщение скалярного умножения. Так, для двумерных систем:
z(x,y) = c(x,y)Ч u(x,y),
где u(x,y) – двумерный входной сигнал, c(x,y) – пространственная маска постоянных (весовых) коэффициентов. Пространственное маскирование представляет собой поэлементное произведение значений сигнала с коэффициентами маски.
Инвариантность систем к сдвигу.
Система называется инвариантной к сдвигу (инвариантной во времени, а равно и по любым другим аргументам), если сдвиг входного сигнала по аргументам вызывает соответствующий сдвиг выходного сигнала:s(x,t) = T[a(x,t)], T[a(x-Dx,t-Dt)] = s(x-Dx,t-Dt).
Это означает, что форма выходного сигнала зависит только от входного сигнала, и не зависит от времени поступления сигнала на вход системы. Инвариантность системы к сдвигу является одним из подтверждений постоянства ее параметров.
Линейность и инвариантность к сдвигу являются независимыми свойствами систем и не определяют друг друга. Так, например, операция квадратирования сигнала (возведения в квадрат всех значений сигнала) инвариантна к сдвигу, но нелинейна.
В теории анализа и обработки данных основное место занимают системы, линейные и инвариантные к сдвигу (ЛИС - системы). Они обладают достаточно широкими практическими возможностями при относительной простоте математического аппарата. В дальнейшем, если это специально не оговаривается, будем иметь в виду именно такие системы.
Преимущество, которое отдается ЛИС - системам в методах обработки информации, базируется на возможности разложения входного сигнала любой, сколь угодно сложной формы, на составляющие простейших форм, отклик системы на которые известен и хорошо изучен, с последующим вычислением выходного сигнала в виде суммы откликов на все составляющие входного сигнала.
Другой важной особенностью ЛИС - систем является то, что любые их комбинации также являются ЛИС - системами, а любую сложную ЛИС - систему можно разложить на комбинации простых систем. Так, например, при последовательном (каскадном) соединении систем, когда выходной сигнал одной системы служит входным сигналом для второй и т.д., образуемая система в целом также является ЛИС - системой, если линейны и инвариантны к сдвигу все системы, в нее входящие, при этом по отношению к общей системной операции преобразования порядок соединения входящих в нее систем значения не имеет.
Математическая модель системы
задается связью между сигналами входа и выхода, и в аналоговой одномерной линейной системе обычно выражается линейным дифференциальным уравнением: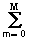 am
am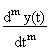 =
=  bn
bn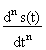 . (4.1.1)
. (4.1.1)
При нормировке к ао = 1, отсюда следует
:y(t) =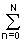 bn
bn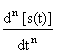 –
– am
am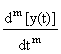 . (4.1.1')
. (4.1.1')
По существу, правой частью этого выражения в самой общей математической форме отображается содержание операции преобразования входного сигнала, т.е. задается оператор трансформации входного сигнала в выходной.
Аналогичная связь в цифровой системе описывается разностными уравнениями
: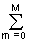 am y((k-m)Dt) =
am y((k-m)Dt) =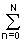 bn s((k-n)Dt). (4.1.2)
bn s((k-n)Dt). (4.1.2)
y(kDt) =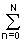 bn s((k-n)Dt) –
bn s((k-n)Dt) – am y((k-m)Dt). (4.1.2')
am y((k-m)Dt). (4.1.2')
Последнее уравнение можно рассматривать как алгоритм последовательного вычисления значений y(k
Dt), k = 0, 1, 2, …, по значениям входного сигнала s(kDt) и предыдущих вычисленных значений y(kDt) при известных значениях коэффициентов am, bn и с учетом задании определенных начальных условий - значений s(kDt) и y(kDt) при k < 0. Интервал дискретизации в цифровых последовательностях отсчетов обычно принимается равным 1, т.к. выполняет только роль масштабного множителя.Нерекурсивные системы.
При нулевых значениях коэффициентов am уравнение (4.1.2') принимает вид:y(k) = bn x(k-n). (4.1.3)
bn x(k-n). (4.1.3)
При установленных значениях коэффициентов b
n значения выходных отсчетов свертки для любого аргумента k определяются текущим и "прошлыми" значениями входных отсчетов. Такая система называется нерекурсивной цифровой системой (НЦС). Нетрудно заметить, что уравнение (4.1.3) полностью повторяет уравнение свертки произвольного сигнала s(k) с импульсным откликом системы h(n), которое уже рассматривалось в теме динамического представления сигналов с базовой позиции "от сигнала". В данном случае, это уравнение получено в более строгой математической форме "от системы" и, как это следует из вышеизложенного, является только частным случаем системного уравнения (4.1.1). Отсюда следует также, что для НЦС импульсным откликом системы является непосредственно ядро свертки bn = hn. Но это действительно только для НЦС. Для систем, описываемых полной формой уравнений (4.1.1) и (4.1.2), импульсный отклик h(n) не равен коэффициентам bn, а зависит и от коэффициентов am, и представляет собой именно отклик системы на единичный входной сигнал.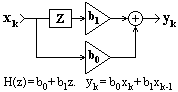
Пример простейшей НЦС приведен на рис. 4.1.2. Интервал суммирования по n получил название "окна" системы. Окно системы (4.1.3) составляет N+1 точку, система является односторонней каузальной, причинно обусловленной текущими и "прошлыми" значениями входного сигнала, выходной сигнал не опережает входного. Каузальная система может быть реализована аппаратно в реальном масштабе времени. При k<n проведение обработки входных данных возможно только при задании определенных начальных условий для точек x(-k), k=1,2,..,N. Как правило, в качестве начальных условий принимаются нулевые значения или значения отсчета х(0). Применяется также четное или нечетное продление функции x(k) на интервал отрицательных значений k. Если при обработке данных начальные интервалы массивов x(k) существенного значения не имеют, то обработку можно начинать с отсчета k=N.
При обработке данных на ЭВМ ограничение по каузальности системного оператора снимается. В программном распоряжении системы могут находиться как "прошлые", так и "будущие" значения входных отсчетов, при этом уравнение (4.1.3) будет иметь вид:
y(k) =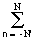 bn x(k-n). (4.1.3')
bn x(k-n). (4.1.3')
При N' = N система называется двусторонней симметричной. Симметричные системы, в отличие от каузальных, не изменяют фазы обрабатываемых сигналов.
Описанный процесс свертки в вещественной области массива данных x(k) с нерекурсивным оператором системы b
n (массивом весовых коэффициентов системы) обычно называют нерекурсивной цифровой фильтрацией данных, а саму систему, если она выполняет только данную операцию, нерекурсивным цифровым фильтром (НЦФ).Пример.
Сглаживание данных скользящим симметричным П-окном размером 5 отсчетов.Уравнение НЦФ: yk =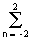 bn xk-n, bn = 0,2. Начальные условия - нулевые.
bn xk-n, bn = 0,2. Начальные условия - нулевые.
Входной сигнал: xk = {0,0,0,0,10,0,10,0,0,0,0}. Выходной сигнал: yk = {0,0,2,2,4, 4, 4,2,2,0,0}.
Проверьте результат (выполните фильтрацию сигнала).
Заметим: сумма коэффициентов
bn сглаживающего НЦФ равна 1, при этом сумма значений выходного сигнала равна сумме значений входного сигнала. Сигнал "размазался" по аргументу.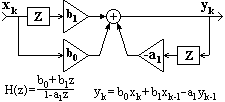
Рекурсивные системы.
Системы, которые описываются полным разностным уравнением (4.1.2), принято называть рекурсивными цифровыми системами (РЦС) или рекурсивными цифровыми фильтрами (РЦФ), так как в вычислении текущих значений выходного сигнала участвует не только входной сигнал, но и значения выходного сигнала, вычисленные в предшествующих циклах расчетов. С учетом последнего фактора рекурсивные системы называют системами с обратной связью. Пример рекурсивной системы приведен на рис. 4.1.3.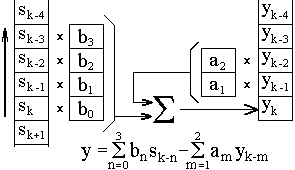
Полное окно рекурсивной системы состоит из двух составляющих: нерекурсивной части b
n,, аналогичной окну нерекурсивной системы и ограниченной в работе текущими и "прошлыми" значениями входного сигнала (при реализации на ЭВМ возможно использование и “будущих” отсчетов сигнала), и рекурсивной части am, которая работает только с "прошлыми", ранее вычисленными значениями выходного сигнала. Техника вычислений для РЦС приведена на рис. 4.1.4.Пример.
Уравнение РЦС: yk= boxk+a1yk-1, при bo=a1=0.5, y-1=0. Входной сигнал: xk = {0, 10, 0, 0, 0,....}.Расчет выходного сигнала:
у
o = 0,5xo + 0,5y-1 = 0 y1 = 0,5x1 + 0,5yo = 5 y2 = 0,5x2 + 0,5y1 = 2.5 y3 = 0,5x3 + 0,5y2 = 1.25y4 = 0,5x4 + 0,5y3 = 0.625 y5 = 0,5x5 + 0,5y4 = 0.3125 и т.д.
Выходной сигнал: yk = {0, 5, 2.5, 1.25, 0.625, 0.3125, 0.15625,...}
Из примера можно видеть, что реакция РЦС на конечный входной сигнал, в принципе, может иметь бесконечную длительность, в отличие от реакции НЦС, которая всегда ограничена количеством членов b
k (окном системы).Пример.
Уравнение РЦС: yk = boxk+a1yk-1+a2yk-2, при bo=a1=a2=1. xk = {0, 1, 0, 0, 0,....}, y-1 = y-2 = 0.Расчет выходного сигнала:
yo = xo+y-1+y-2 = 0. y1 = x1+yo+y-1 = 1. y2 = x2+y1+yo = 1. y3 = x3+y2+y1 = 2.
y4 = x4+y3+y2 = 3. y5 = x5+y4+y3 = 5. y6 = x6+y5+y4 = 8. y7 = x7+y6+y5
= 13. и т.д.Заметим: сумма коэффициентов обратной связи a
i больше 1 и выходной сигнал идет "в разнос".Пример. Интегрирование данных по формуле трапеций.
Уравнение РЦФ: y
k=(xk+xk-1)/2+yk-1, начальные условия - нулевые.Входной сигнал: x
k={0,0,2,2,8,0,4,4,0,..}.Выполните фильтрацию. Контроль: y
k= {0,0,1,3,8,12,14,18,20,20,...}.4.2. Нерекурсивная фильтрация сигналов
Предмет фильтрации сигналов является основной областью применения нерекурсивных систем. Под фильтрацией будем понимать любое преобразование, при котором во входных сигналах целенаправленно изменяются определенные соотношения (динамические или частотные) между различными компонентами этих сигналов.
К операциям фильтрации информации традиционно относят операции сглаживания, прогнозирования, дифференцирования, интегрирования и разделения сигналов, а также выделение информационных (полезных) сигналов и подавление шумов (помех). Основным методом фильтрации данных являются частотная селекция сигналов. Системы, выполняющие операции фильтрации, обычно называют фильтрами.
Операция свертки сигнала с ядром (оператором) фильтра отображается в частотной области умножением спектра сигнала на частотный образ оператора фильтра. Тем самым, мы получаем возможность целенаправленно изменять спектр сигнала. Например, в звукозаписи изменение спектра сигнала позволяет очищать запись от шумов, компенсировать искажения сигнала различными устройствами звукозаписи, менять тембры инструментов. При обработке изображений фильтрация позволяет применять к изображению разные эффекты: размытие, подчеркивание границ, тиснение и пр. В самых различных областях фильтрация часто служит для разделения сигналов, смешанных в один, очищения сигнала от шумов, а также является составным компонентом многих других, более сложных процессов.
Частотные характеристики фильтров. В общем случае, фильтр меняет в спектре сигнала и амплитуды, и фазы гармоник. Однако фильтры можно проектировать так, чтобы они или не меняли фазу сигнала, или сдвигали все гармоники сигнала по времени на одну и ту же величину (сдвигали во времени весь сигнал). Такие фильтры называют фильтрами с линейной фазой.
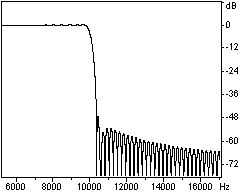
Основное свойство фильтра – его амплитудно-частотная и фазочастотная характеристики (АЧХ и ФЧХ). Они показывают, какое влияние фильтр оказывает на амплитуду и фазу различных гармоник обрабатываемого сигнала. Если фильтр имеет линейную фазу, то рассматривается только АЧХ фильтра. Обычно частотная характеристика изображается в виде графика зависимости амплитуды от частоты (в децибелах). Так, если фильтр пропускает все сигналы в какой-либо полосе частот без изменения (коэффициент передачи равен 1), то это отображается значением 0 дБ. Подавление каких либо частот отображается со знаком минус (в 2 раза
Ю -6 дБ, в 10 раз Ю -20 дБ, в 100 раз Ю -40 дБ), а усиление, соответственно, со знаком плюс. Пример частотной характеристики фильтра приведен на рис. 4.2.1.В зависимости от общего вида частотной характеристики можно выделяют следующие распространенные типы фильтров: НЧ-фильтры (
low-pass filters), ВЧ-фильтры (high-pass filters), полосовые фильтры, которые пропускают (band-pass filters) или подавляют (band-reject filters) сигнал только в определенной частотной полосе. Существуют и другие типы фильтров с более сложными частотными характеристиками.Обычно в задачах фильтрации сигнала задается требуемая частотная характеристика фильтра. Построить в точности заданный фильтр обычно бывает не так просто. Тогда строится фильтр, близкий по характеристикам к заданному.
Например, невозможно построить идеальный фильтр низких частот, который пропускает без изменения все сигналы ниже определенной частоты (в полосе пропускания, pass band) и полностью подавляет все сигналы выше этой частоты (в полосе подавления или непропускания, stop band). Такой фильтр реализуется оператором бесконечно большого размера. Реальные фильтры низких частот обладают плавным переходом от полосы пропускания (0 дБ с максимально возможными отклонениями обычно не более ±0.5 дБ) к полосе подавления, где сигнал подавляется, как правило, более чем в 100-1000
раз (рис. 4.2.1). Крутизна спада и значения подавления после спада определяются конкретными требованиями к фильтру.В пределе, частотная характеристика фильтра может задаваться произвольной кривой. Например, фильтр может иметь несколько частотных полос пропускания с разными коэффициентами усиления, разделенных полосами с разными коэффициентами подавления.
Расчет операторов нерекурсивных фильтров.
Существует много способов построения фильтров с заданной частотной характеристикой. Наиболее универсальный и, в то же время, наиболее простой – проектирование фильтров путем обратного преобразования Фурье требуемой частотной характеристики фильтра. Рассмотрим этот способ подробнее на примере чисто технической задачи формирования сигналов с высоким временным разрешением на выходе детекторов излучения.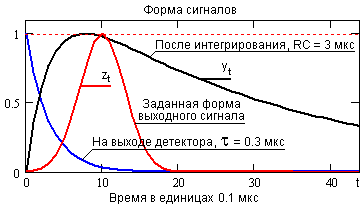
Сигналы регистрации ионизирующих частиц формируются интегрированием заряда, в который трансформируется энергия частиц при ее поглощении в рабочей среде детектора. Идентификация энергии частиц по зарегистрированным сигналам обеспечивается при полном сборе заряда на выходе детектора, при этом постоянная времени RC интегрирования заряда на выходной RC-цепи детектора должна быть на порядок больше времени преобразования энергии в детекторе. На рис. 4.2.2 приведен пример формы выходных сигналов детектора до и после сбора зарядов при постоянной
t = 0.3 мкс выхода заряда и RC = 3 мкс интегрирования заряда. Амплитуды сигналов нормированы по максимуму для наглядности сравнения.Для исключения ошибок измерений при возможных наложениях последующих сигналов на спад предыдущих применяются различные способы укорочения сигналов y(t) и быстрого восстановления нулевой линии. Применение нерекурсивного формирующего фильтра позволяет решить эти задачи просто и эффективно.
Допустим, что необходимо превратить выходной сигнал y(t) в короткий и удобный для измерения амплитудных значений сигнал z(t), форма которого приведена на рис. 4.2.2. Это можно выполнить операций свертки:
z(t) = h(t) * y(t),
для чего требуется определить соответствующий оператор преобразования h(t). Переведем левую и правую часть уравнения свертки в спектральную область:
Z(f) = H(f)·Y(f). (4.2.1)
Отсюда, частотная характеристика и функция требуемого оператора свертки определяются выражениями:
H(f) = Z(f) / Y(f). (4.2.2)
H(f) « h(t). (4.2.3)
Возможность реализации оператора h(t) определяется устойчивостью решения уравнения (4.2.2) и зависит от частотных характеристик сигналов y(t) и z(t). К числу обязательных условий реализации следует отнести отсутствие полюсов функции Y(f) для исключения деления на ноль, и более быстрое затухание функции Z(f) по сравнению с функцией Y(f). В качестве сигнала z(t) целесообразно задавать функцию Гаусса такой ширины (на половине своей высоты), спектр которой Z(f) по своей основной значимой части соизмерим со спектром сигнала Y(f). Чем меньше ширина функции Гаусса, тем лучше будет выполняться сжатие сигнала, однако при чрезмерном сжатии и, соответственно, увеличении высокочастотных составляющих в Z(
f), оператору h(t) придется осуществлять существенный подъем высокочастотных составляющих сигнала y(t), что приведет к увеличению коэффициента усиления фильтром дисперсии помех. С учетом каузальности работы формирующих фильтров выходные сигналы должен задаваться за пределами фронта сигнала y(t), а экстремумы сигналов – за пределами экстремума входного сигнала.В силу линейности фильтра и принципа суперпозиции зарядов на интегрирующей емкости, в любой текущей временной точке оператор фильтра реагирует на разряд интегрирующей емкости, как на сумму разрядов от всех предыдущих импульсов. И если по разряду одного импульса система будет точно настроена на нулевую линию, то она будет сохранять нулевую линию независимо от количества и времени прихода импульсов, а равно и от наложения импульсов друг на друга.
Форма сигнала y(t) в первом приближении соответствует выражению:
y(t) = exp(-t/RC) - exp(-t/t). (4.2.4)
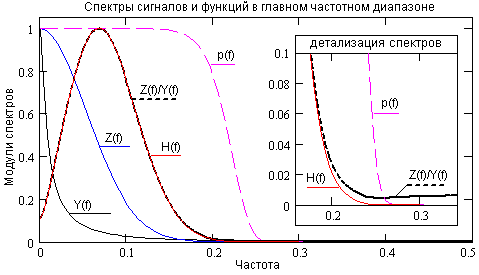
Основная информация сигнала заключена в его фронте, и в спектральной области формирует высокочастотные составляющие сигнала. На рис. 4.2.3 приведены модули спектров Y(f) и Z(f) сигналов y(t) и z(t), и частотные передаточные функции оператора фильтра Z(f)/Y(f). Для наглядного представления их формы все модули нормированы к 1 по максимальным значениям. Значимую часть спектра формируемого оператора целесообразно выделить умножением спектра оператора на какую-либо весовую функцию p(t), равную 1 в пределах значимой части отношения Z(f)/Y(f), и достаточно плавно спадающую к нулю за его границами (окно детализации на рисунке). Одновременно это подавит высокочастотные шумы в сигнале y(t), появление которых в регистрируемом сигнале неизбежно в силу природы ионизирующего излучения. В результате мы получим спектральную функцию H(f) требуемого оператора преобразования сигналов.
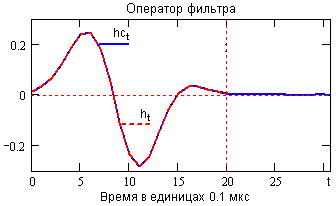
Временная функция оператора фильтра h(t) вычисляется обратным преобразованием Фурье функции H(f). Для начала длина оператора устанавливается соизмеримой с длиной входного сигнала (оператор hc(t) на рис. 4.2.4). В данном случае оператор фильтра является конечным, достаточно быстро затухает, и может быть ограничен до величины h(t). В общем случае, для изрезанных и скачкообразных функций H(f), оператор фильтра может затухать достаточно медленно и может потребоваться его усечение до определенных конечных размеров с применением весовых функций.
В принципе, по заданной частотной характеристике H(f) может быть синтезирован аналоговый фильтр, но настройка такого фильтра под конкретные параметры детектора, будет представлять собой достаточно трудоемкую операцию. Больше возможностей в этом отношении представляют дискретные методы преобразования сигналов. Ограничение размеров дискретных операторов определяется допустимой погрешностью реконструкции заданной формы сигналов и точностью формирования нулевой линии при заданном временном разрешении.
Работоспособность фильтра проверяется сверткой оператора с сигналом y(t). На рис. 4.2.5 приведено сопоставление заданной формы сигнала z(t) и формы сигнала zh(t) на выходе фильтра при подаче на его вход сигнала y(t). Фильтр был смоделирован в цифровой форме с шагом
Dt=0.1 мкс с размером окна N=20. Оператор фильтра имел коэффициент передачи постоянной составляющей Кпс = 0.2 и коэффициент усиления дисперсии шумов 0.85.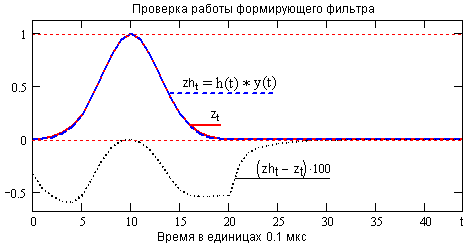
На рисунке приведена также абсолютная погрешность реконструкции сигнала
Dz(t)=zh(t)-z(t), увеличенная для наглядности в 100 раз. Погрешность реконструкции флангов сигнала при амплитудных измерениях значения не имеет. Гораздо большее значение имеет быстрое и точное восстановление нулевой линии после формирования выходного сигнала, которое определяет погрешность измерения амплитуды последующего сигнала, наложенного на разряд интегрирующей емкости от предыдущего. Компенсация погрешностей, возникающих за счет усечения спектров и ограничения размеров самого оператора, может проводиться коррекцией значения последнего члена оператора (выход на нулевую линию), а коррекцией значения первого члена оператора может настраиваться точное соотношение 1:1 амплитуд входных и выходного сигналов.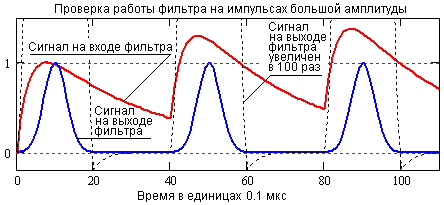
Реконструкция сигналов, приведенная на рис. 4.2.5, обеспечила временное разрешение измерений 3-4 мкс при точности амплитудных измерений 0.1%. На рис. 4.2.6 приведена проверка временного разрешения фильтра на модели сигнала в виде трех последовательных импульсов одинаковой и достаточно большой амплитуды, следующих через 4 мкс друг за другом и вызывающих значительное смещение напряжения на интегрирующей емкости RC-цепи. Пунктиром на рисунке приведено восстановление нулевой линии на выходе фильтра с увеличением масштаба в 100 раз.
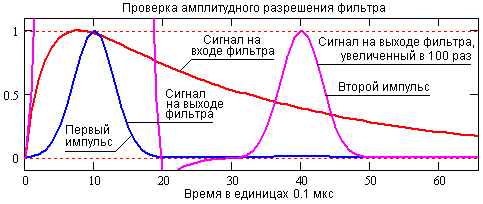
Точность реконструкции сигналов при разных значениях амплитуд входных сигналов можно видеть на рис. 4.2.7. На модели установлено отношение амплитуд 100:1 первого и второго импульсов. Второй импульс, наложенный на спад первого импульса, практически не отражается на его форме. Фильтр уверенно разделяет эти импульсы с ошибкой формирования амплитуды второго импульса не более 1%.
литература
1. Баскаков С.И. Радиотехнические цепи и сигналы
: Учебник для вузов. - М.: Высшая школа, 1988.18. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. – М.: Связь, 1979. – 416 с.
22. Сиберт У.М. Цепи, сигналы, системы. – М.: Мир, 1988. – 336 с.
25. Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2003. – 608 с.
31. Лукин. А. Введение в цифровую обработку сигналов. – М.: МГУ, 20
02.Copyright ©2006 Davydov А.V.
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|
