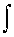exp(jwt) dt = (1/jw) exp(jwt), H(w) = 1/jw.Понятие собственных функций. Удобство использования частотного представления сигналов заключается в том, что гармонические функции являются собственными функциями операций переноса, интегрирования, дифференцирования и других линейных операций, инвариантных по координатам. Они проходят через линейные системы, не изменяя формы, а изменяют лишь фазу и амплитуду.
Допустим, что исходная функция является линейной комбинацией функций синуса и косинуса:
s(х) = А sin(х)+B cos(х).
Осуществим произвольный сдвиг функции по аргументу на величину h. При этом получаем:
s(х+h) = C sin(х)+D cos(х),
C = А cos(h) – B sin(h),
D = A sin(h) + B cos(h),
где коэффициенты C и D, как и в исходном выражении коэффициенты А и В, не зависят от аргумента, при этом C
2+D2 = А2+В2. Таким образом, при произвольном переносе функции по аргументу (а равно и при интегрировании, дифференцировании и других линейных преобразованиях) любую линейную комбинацию синуса и косинуса можно представить линейной комбинацией этих же функций.Экспоненциальная комплексная запись гармонических функций
делает это свойство еще нагляднее. Для произвольной гармонической функции имеем:cos(wt-j) = A cos(wt)+B sin(wt),
где A = cos(
j), B = sin(j), j - начальный фазовый угол колебания при t = 0. Переходя к комплексной записи данной функции с использованием тождеств Эйлераcos(wt) = [ехр(jwt)+exp(-jwt)]/2, sin(wt) = [ехр(jwt)-exp(-jwt)]/2j,
получаем:
cos(wt-j) = C exp(jwt)+C*exp(-jwt),
где: C = 0,5 exp(-j
j), C* = 0,5 exp(jj) – величина, комплексно сопряженная с С. Применяя в качестве гармонической составляющей разложения сигнала функцию ехр(jwt), можно рассматривать вторую функцию ехр(-jwt), комплексно сопряженную с первой, как такую же составляющую, но с отрицательной частотой. Естественно, что отрицательная частота является чисто математической абстракцией, но нужно помнить, что пара таких комплексно сопряженных составляющих в сумме всегда дает вещественную функцию.Экспоненциальные функции также являются собственными функциями линейных операций. Для операции переноса с использованием экспоненциальных функций:
exp[jw(t+h)] = exp(jwh)·exp(jwt) = H(w) exp(jwt),
где Н(
w) = exp(jwh) - собственное значение операции переноса, независимое от переменной.Для операции дифференцирования:
d[exp(jwt)]/dt = jw exp(jwt), H(w) = jw.
Для операции интегрирования:
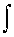exp(jwt) dt = (1/jw) exp(jwt), H(w) = 1/jw.
В общей форме, для любых линейных операций преобразования:
Т[exp(j
wt)] = H(w) exp(jwt),где T[.] - произвольный линейный оператор, H(
w) - собственное значение операции, независимое от аргумента.У специалистов - практиков существует предубеждение против использования комплексных функций с их мнимыми частотами. Поэтому в дальнейшем будем использовать и вещественные функции, и их комплексные аналоги, по крайней мере, до тех пор, пока простота и удобство использования последних не станет очевидным.
Ряды Фурье.
Разложению в ряды Фурье подвергаются периодические сигналы. Периодическую функцию любой формы, заданную на интервале одного периода Т = b-a и удовлетворяющую на этом интервале условиям Дирехле (ограниченная, кусочно-непрерывная, с конечным числом разрывов 1-го рода), можно представить в виде ряда Фурье: s(t) =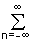
Sn exp(jnDwt), Sn = S(nDw), Dw = 2p/T, (4.1.1)
где весовые коэффициенты S
n ряда определяются по формуле: Sn = (1/T)
s(t) exp(-jnDwt) dt. (4.1.2)
Ряд Фурье представляет собой ансамбль комплексных экспонент exp(jn
Dwt) с частотами, образующими арифметическую прогрессию. Функцию весовых коэффициентов S(nDw) принято называть комплексным спектром периодического сигнала или фурье-образом функции s(t). Спектр периодического сигнала является дискретной функцией, т.к. он определен только для целых значений n с шагом по частоте, обратным периоду: Dw = 2p/Т (или Df = 1/T). Первую частотную составляющую спектра при n = 1, равную w1 = 1Ч Dw = 2p/T (или f1 = 1/T), называют основной частотой сигнала (первой гармоникой), остальные частоты дискретного спектра nw1 при n>1 называют гармониками сигнала. Значения S(nDw) по положительным и отрицательным значениям n являются комплексно сопряженными. Шаг по частоте Dw между двумя соседними синусоидами из разложения Фурье называется частотным разрешением спектра.С чисто математических позиций множество функций ex
p(jnDwt), -Ґ < n < Ґ образует бесконечномерный базис линейного пространства L2[a,b] ортогональных синус-косинусных функций, а коэффициенты Sn по (4.1.2) представляют собой проекции сигнала s(t) на эти базисные функции. Соответственно, сигнал s(t) в форме ряда Фурье (4.1.1) – это бесконечномерный вектор в пространстве L2[a,b], точка с координатами Sn по базисным осям пространства exp(jnDwt).Подынтегральную функцию экспоненты в выражении (4.1.2) с использованием тождества Эйлера
exp(±jwt) = cos(wt) ± jЧ sin(wt)
можно разложить на косинусную и синусную составляющие и выразить комплексный спектр в виде действительной и мнимой части:
Sn = (1/T)s(t) [cos(nDwt) - j sin(nDwt)] dt = Аn - jBn. (4.1.3)
An ≡ A(nDw) = (1/T)s(t) cos(nDwt) dt, (4.1.4)
Bn ≡ B(nDw) = (1/T) s(t) sin(nDwt) dt. (4.1.5)
На рис. 4.1.1 приведен пример периодического сигнала (прямоугольный импульс на интервале (1-3.3), повторяющийся с периодом Т=40) и форма действительной и мнимой части его спектра. Обратим внимание, что действительная часть спектра является четной относительно нуля функцией A(n
Dw) = A(-nDw), так как при вычислении значений A(nDw) по формуле (4.1.4) используется четная косинусная функция cos(nDwt) = cos(-nDwt). Мнимая часть спектра является нечетной функцией B(nDw) = -B(-nDw), так как для ее вычисления по (4.1.5) используется нечетная синусная функция sin(nDwt) = - sin(-nDwt).
Рис. 4.1.1. Сигнал и его комплексный спектр.
Комплексные числа дискретной функции (4.1.3) могут быть представлены в виде модулей и аргументов комплексной экспоненты, что дает следующую форму записи комплексного спектра:
Sn = Rn exp(jjn), (4.1.3')
Rn2 ≡ R2(nDw) = A2(nDw)+B2(nDw),
j
n ≡ j(nDw) = arctg(-B(nDw)/A(nDw)).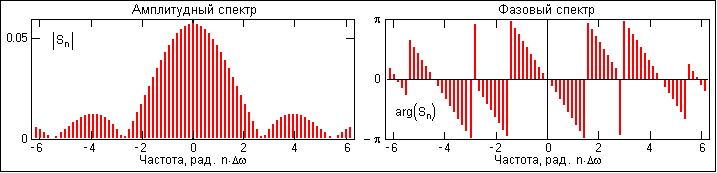
Рис. 4.1.2. Модуль и аргумент спектра.
Модуль спектра R(n
Dw) называют двусторонним спектром амплитуд или АЧХ - амплитудно-частотной характеристикой сигнала, а аргумент спектра (последовательность фазовых углов j(nDw)) - двусторонним спектром фаз или ФЧХ – фазово-частотной характеристикой. Спектр амплитуд всегда представляет собой четную функцию: R(nDw) = R(-nDw), а спектр фаз нечетную: j(nDw) = -j(-nDw). Пример спектра в амплитудном и фазовом представлении для сигнала, показанного на рис. 4.1.1, приведен на рис. 4.1.2. При рассмотрении спектра фаз следует учитывать периодичность 2p угловой частоты (при уменьшении фазового значения до величины менее -p происходит сброс значения -2p).Если функция s(t) является четной, то все значения B(n
Dw) по (4.1.5) равны нулю, т.к. четные функции ортогональны синусным гармоникам и подынтегральное произведение s(t)·sin(nDwt) дает нулевой интеграл. Следовательно, спектр функции будет представлен только вещественными коэффициентами. Напротив, при нечетности функции s(t) обнуляются все значения коэффициентов А(nDw) (нечетные функции ортогональным косинусным гармоникам) и спектр является чисто мнимым. Этот фактор не зависит от выбора границ задания периода функции на числовой оси. На рис. 4.1.3(А) можно наглядно видеть ортогональность первой гармоники синуса и четной функции, а на рис. 4.1.3(В) соответственно косинуса и нечетной функции в пределах одного периода. Учитывая кратность частот последующих гармоник первой гармонике спектра, ортогональность сохраняется для всех гармоник ряда Фурье.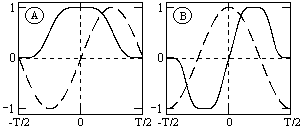
Рис. 4.1.3. Ортогональность функций.
При n = 0 имеем В
о = 0, и получаем постоянную составляющую сигнала:S0 ≡ Ao ≡ Ro ≡ (1/T) s(t) dt.
Тригонометрическая форма рядов Фурье.
Объединяя в (4.1.1) комплексно сопряженные составляющие (члены ряда, симметричные относительно центрального члена ряда S0), можно перейти к ряду Фурье в тригонометрической форме:s(t) = Ао
+2
(An cos(nDwt) + Bn sin(nDwt)), (4.1.6) Rn cos(nDwt + jn). (4.1.6')
Значения A
n, Bn вычисляются по формулам (4.1.4-4.1.5), значения Rn и jn - по формулам (4.1.3').Ряд (4.1.6) представляют собой разложение периодического сигнала s(t) на сумму вещественных элементарных гармонических функций (косинусных и синусных) с весовыми коэффициентами, удвоенные значения которых (т.е. значения 2
Ч An, 2Ч Bn) не что иное, как амплитуды соответствующих гармонических колебаний с частотами nDw. Совокупность амплитудных значений этих гармоник образует односторонний физически реальный (только для положительных частот nDw) спектр сигнала. Для сигнала на рис. 4.1.1, например, он полностью повторяет правую половину приведенных на рисунке спектров с удвоенными значениями амплитуд (за исключением значения Ао на нулевой частоте, которое, как это следует из (4.1.6), не удваивается). Но такое графическое отображение спектров используется довольно редко (за исключением чисто технических приложений).Более широкое применение для отображения физически реальных спектров находит формула (4.1.6'). Спектр амплитуд косинусных гармоник при таком отображении называется амплитудно-частотным составом сигнала, а спектр фазовых углов гармоник – фазовой характеристикой сигнала. Форма спектров повторяет правую половину соответствующих двусторонних спектров (см. рис. 4.1.2) также с удвоенными значениями амплитуд. Для четных сигналов отсчеты фазового спектра могут принимать только значения 0 или
p, для нечетных соответственно ± p/2.Ряды Фурье произвольных аналоговых периодических сигналов могут содержать бесконечно большое количество членов. Однако одним из важных достоинств преобразования Фурье является то, что при ограничении (усечении) ряда Фурье до любого конечного числа его членов обеспечивается
наилучшее по средней квадратической погрешности приближение к исходной функции (для данного количества членов).На рис. 4.1.4 показано разложение в комплексный ряд Фурье модельного сигнала, выполненное в среде Mathcad. Модель сигнала задана с тремя разрывами первого рода (скачками). Любой скачок функции содержит все частоты диапазона до бесконечности, в связи с чем ряд Фурье также бесконечен и очень медленно затухает. На рисунке приведены значения только первых 100 членов ряда, при этом график спектра сигнала, как это обычно принято на практике, построен в виде огибающей значений модулей коэффициентов ряда S
n и только по области положительных значений n.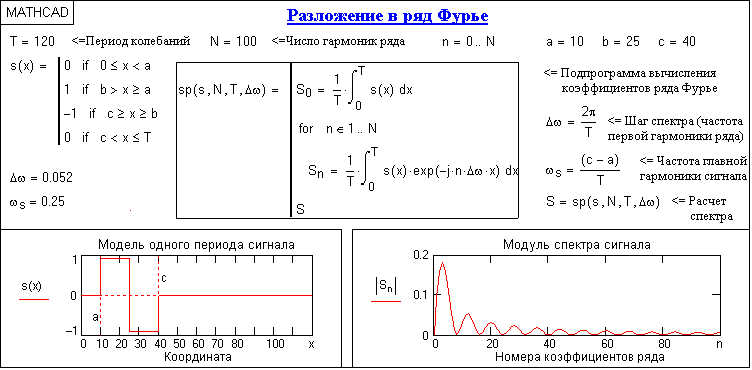
Рис. 4.1.4. Разложение сигнала в комплексный ряд Фурье.
Программа на рис. 4.1.5 продолжает программу рис. 4.1.4 и показывает реконструкцию сигнала по его спектру при ограничении числа членов ряда Фурье.
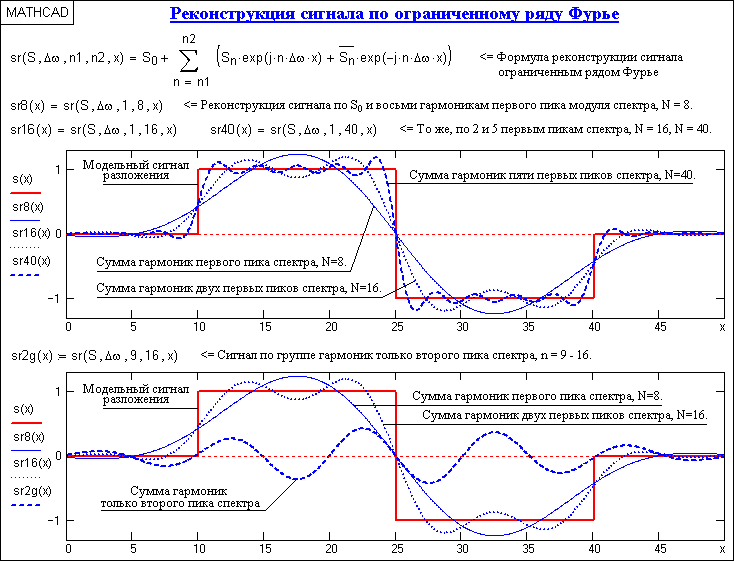
Рис. 4.1.5. Реконструкция сигнала (продолжение программы на рис. 4.1.4)
На верхнем графике рисунка приведен реконструированный сигнал при N = 8 (гармоники первого пика спектра, центр которого соответствует главной гармонике сигнала и члену ряда n =
ws/Dw), N = 16 (гармоники двух первых пиков) и N=40 (пять первых пиков спектра). Естественно, что чем больше членов ряда включено в реконструкцию, тем ближе реконструированный сигнал к форме исходного сигнала.Принцип последовательного приближения к исходной форме наглядно виден на нижнем графике рисунка. На нем же можно видеть и причины появления пульсаций на реконструкции скачков функций, которые носят название эффекта Гиббса. При изменении количества суммируемых членов ряда эффект Гиббса не исчезает. Не изменяется также относительная амплитуда пульсаций (по отношению к амплитуде скачка) и относительное затухание (по коэффициенту последовательного уменьшения амплитуды пульсаций по отношению к максимальному выбросу), изменяется только частота пульсаций, которая определяется частотой последних суммируемых гармоник.
Эффект Гиббса имеет место всегда при резких нарушениях монотонности функций. На скачках эффект максимален, во всех других случаях амплитуда пульсаций зависит от характера нарушения монотонности функции. Пример явления Гиббса для радиоимпульса приведен на рис. 4.1.6 (использована программа на рис. 4.1.4, точками показан реконструированный сигнал с увеличением масштаба в 10 раз).
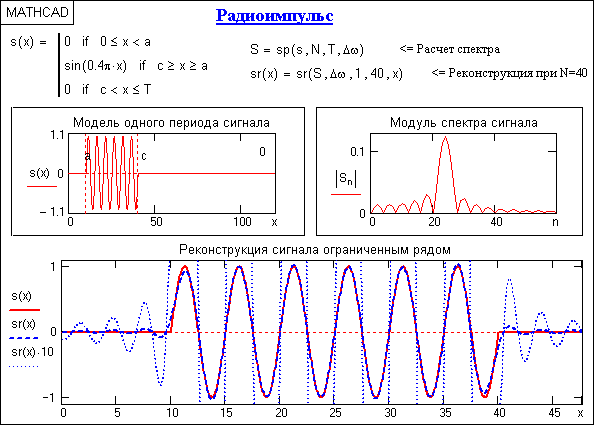
Рис. 4.1.6.
На рис. 4.1.7 приведен пример разложения в ряд Фурье одного периода T=(a,c) модельного периодического сигнала sq(x), представленного информационным сигналом s(x) в сумме с шумовым сигналом. Спектр шумов близок к спектру белого шума (равномерное распределение энергии шумов по всем частотам спектра).
На спектре модельного сигнала достаточно четко выделяется диапазон частот информационного сигнала. Реконструкция сигнала с ограничением ряда Фурье гармониками только информационного сигнала (сигнал sr5(x), N=5) дает сглаженную форму сигнала по минимуму среднеквадратического расхождения с модельным сигналом для данного количества членов ряда, но только по периоду разложения (а, с), и наиболее точное приближение к информационному сигналу. При увеличении в реконструкции количества членов ряда Фурье восстановленный сигнал начинает приближаться к модельному сигналу, но только по данному периоду T=(a,c), при этом расхождение с информационным сигналом увеличивается. Заметим, что спектр сигнала может определяться и по нескольким периодам сигнала, что повышает точность реконструкции информационного сигнала.
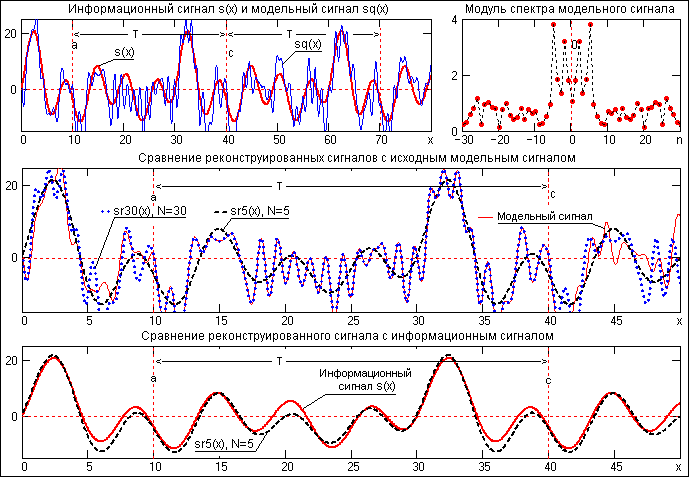
Рис. 4.1.7.
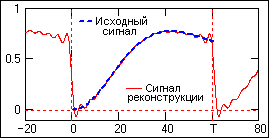
В ряд Фурье может разлагаться и произвольная непериодическая функция, заданная (ограниченная, вырезанная из другого сигнала, и т.п.) на интервале (a,b), если нас не интересует ее поведение за пределами данного интервала. Однако следует помнить, что применение формул (4.1.1-4.1.6) автоматически означает периодическое продолжение данной функции за пределами заданного интервала (в
обе стороны от него) с периодом Т = b-a. Однако при этом на краях интервала может возникнуть явление Гиббса, если уровень сигнала на краях не совпадает и образуются скачки сигнала при его периодическом повторении, как это видно на рис. 4.1.8. При разложении исходной функции в ограниченный ряд Фурье и его обработке в частотной области на самом деле при этом обрабатывается не исходная функция, а реконструированная из ограниченного ряда Фурье.При усечении рядов Фурье определенное искажение функций существует всегда. Но при малой доле энергии отсекаемой части сигнала (при быстром затухании спектров функций) этот эффект может быть и мало заметен. На скачках и разрывах функций он проявляется наиболее ярко.
Параметры эффекта Гиббса.
Большинство методов анализа и обработки сигналов представляют собой или имеют в своем составе операцию свертки сигналов с функцией оператора свертки. Как сигнал, так и оператор свертки, выполняющий определенную задачу обработки данных и реализующий определенную частотную функцию системы обработки, могут быть бесконечно большими. Практика же обработки на ЭВМ может иметь дело только с ограниченными множествами и данных, и коэффициентов оператора. В общем случае, эти ограниченные множества "вырезаются" из бесконечных множеств, а разложение в ряды Фурье, также ограниченные по размерам, является одной из самых распространенных операций обработки цифровых множеств. С учетом этого рассмотрим явление Гиббса более подробно, т.к. при любых ограничениях рядов Фурье оно всегда может весьма существенно сказаться на качестве и точности обработки сигналов.Очевидно, что при усечении ряда Фурье (4.1.1) любой функции до конечного числа членов N мы будем иметь усеченный ряд Фурье:
sN(x) =
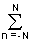S(n) exp(jxnDw), (4.1.7)
при этом происходит усечение спектральной характеристики функции до частоты n
Dw и сходимость суммы остающихся членов ряда sN(x) к исходной функции s(x) ухудшается в тем большей степени, чем меньше значение N. Особенно ярко это проявляется на крутых перепадах (разрывах, скачках) функций:- крутизна перепадов "размывается", т.к. она не может быть больше, чем крутизна (в нулевой точке) последней сохраненной гармоники ряда (4.1.7);
- по обе стороны "размытых" перепадов появляются выбросы и затухающие осцилляции с частотой, равной частоте последнего сохраненного или первого отброшенного члена ряда (4.1.7).
Рассмотрим явление Гиббса на примере разложения в ряд Фурье функции единичного скачка s(x), которая имеет разрыв величиной 1 в точке х = 0. Уравнение функции:
s(x) = -0.5 при –T/2 ≤ x < 0; s(x) = 0.5 при 0 Ј x ≤ T/2.
Поскольку функция является нечетной, ее ряд Фурье не содержит косинусных членов, и коэффициенты ряда в односторонней тригонометрической форме определяются выражением (с учетом соотношения
Dw = 2p/T):bn = (2/T)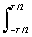 
s(x) sin(xnDw) dx = (2/T) 
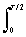sin(xnDw) dx.
bn = 2/(n·p), n- нечетное,
bn = 0, n- четное.
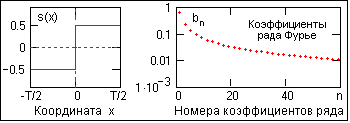
Рис. 4.1.9. Значения коэффициентов b
n.Как видно на рис. 4.1.9, ряд коэффициентов b
n затухает очень медленно. Соответственно, медленно будет затухать и ряд Фурье функции s(x):s(x) = (2/p)[sin xDw + (1/3)·sin x3Dw + (1/5)·sin x5Dw +....].
s(x) = (2/p)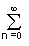
sin[x(2n+1)Dw]/(2n+1). (4.1.8)
Этот ряд при усечении до M нечетных членов можно записать в следующем виде:
s(x) = (2Dw/p)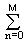
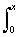cos(x(2n+1)Dw) dx = (2Dw/p)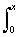[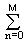cos(x(2n+1)Dw)] dx.
Сумма косинусного ряда равна sin[2(M+1)x
Dw]/(2sin xDw). Отсюда:sM(x) =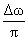 
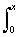
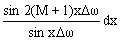. (4.1.9)
Для определения местоположения максимумов и минимумов возникающих осцилляций функции, приравняем к нулю ее первую производную (подынтегральную функцию) выражения (4.1.9), при этом:
xk = ± kp/(2Dw(M+1)) = ± kT/(4(M+1)) , k = 1,2,...
Соответственно, амплитудные значения первых (максимальных) осцилляций функции приходится на точки x
k=1 = ± T/(4(M+1)), вторых (противоположных по полярности) - на точки xk=2 = ± T/(2(M+1)). Период пульсаций равен xk=3-xk=1 ≡ 2xk=1 = ± T/(2(M+1)), т.е. на одном периоде задания сигнала появляется 2(М+1) пульсация с частотой, обратным периоду и равной 2(M+1)Df – частоте последнего сохраненного в суммировании члена ряда Фурье. Функция пульсаций (при ее выделении) является нечетной относительно скачка. Соответственно, при скачке функции s(x) на точке периода Т значения хk являются значениями Dxk относительно точки скачка. Амплитудные значения функции в точках х1 и х2 (при подстановках х1 и х2 верхним пределом в (4.1.9)) практически не зависят от количества членов ряда М и равны:sM(x1) » 0.5+0.09, sM(x2) » 0.5-0.05.
Амплитуда последующих осцилляций постепенно затухает.
Реконструкция скачка при трех значениях ряда приведена на рис. 4.1.10. Как и положено, функция продолжается периодически за пределами заданного интервала (-Т/2, Т/2), при этом на границах периодов также образуются скачки. Скачки являются центрами возникающих осцилляций. Наложение осцилляций друг на друга в зависимости от расстояния между их центрами может как уменьшать амплитуду пульсаций, так и увеличивать.
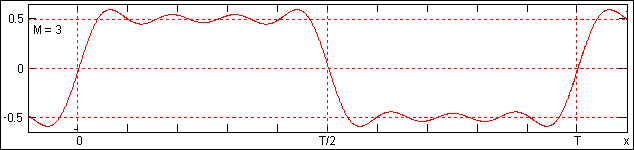
Рис. 4.1.10. Реконструкция скачка по ограниченному раду Фурье при М
=3.Таким образом, для усеченных рядов Фурье предельные значения максимальных выбросов по обе стороны от скачка и следующих за ними обратных выбросов при единичной амплитуде разрыва функции достигают соответственно 9% и 5% значения амплитуды скачка. Кроме того, сам скачок функции из собственно скачка преобразуется в переходную зону, длина которой между точками максимальных выбросов по обе стороны скачка равна T/(2(M+1)), а по уровню исходных значений функции на скачке (в данном случае от -0.5 до 0.5) порядка (2/3)T/(2(M+1)). Это явление типично для всех функций с разрывами.
|
|
 |
