Энтропия непрерывного источника информации
Энтропия непрерывного источника информации должна быть бесконечна, т. к. неопределенность выбора из бесконечно большого числа возможных состояний бесконечно велика. (на самом деле это только некорректная математическая модель, так как реальные сигналы занимают ограниченный спектр частот, а значит, могут быть представлены дискретными значениями через некоторый шаг, определяемый теоремой Котельникова; кроме того реальные сигналы не могут быть измерены с бесконечной точностью, так как имеются шумы линии и ошибка измерения, а это значит, что по шкале динамического диапазона непрерывный сигнал тоже может быть представлен конечным числом различимых квантовых уровней - примечание К.А. Хайдарова)
Разобьем диапазон изменения непрерывной случайной величины U на конечное число n малых интервалов Du. При реализации значений u в интервале (un, un+Du) будем считать, что реализовалось значение un дискретной случайной величины U', вероятность реализации которой:
p(un<u<un+Du) =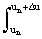
p(u) du » p(un) Du.
Энтропия дискретной величины U':
H(U') = -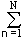
p(un) Du log (p(un) Du).
Заменяем log (p(u
n) Du) = log p(un)+log Du, принимаем во внимание, что сумма p(un)Du по всем возможным значениям un равна 1, и получаем:H(U') = -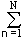p(un) Du log p(un) – log Du. (1.4.4)
В пределе, при
Du ® 0, получаем выражение энтропии для непрерывного источника:H(U) = -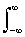
p(u) log p(u) du –
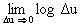. (1.4.5)
Значение энтропии в (1.4.5), как и ожидалось, стремится к бесконечности за счет второго члена выражения. Для получения конечной характеристики информационных свойств непрерывных сигналов используют только первый член выражения (1.4.5), получивший название дифференциальной энтропии
. Ее можно трактовать, как среднюю неопределенность выбора произвольной случайной величины по сравнению со средней неопределенностью выбора случайной величины U', имеющей равномерное распределение в диапазоне (0-1). Действительно, для такого распределения p(un) = 1/N, Du = 1/N, и при N ® Ґ из (1.4.4) следует:H(U') = - (log N)/N - log Du ® -.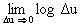
Соответственно, разность энтропий дает дифференциальную энтропию:
h(U) = H(U) – H(U') = -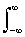p(u) log p(u) du. (1.4.6)
Дифференциальная энтропия не зависит от конкретных значений величины U:
h(U+a) = h(U), a = const,
но зависит от масштаба ее представления:
h(kU) = h(U) + log k.
Практика анализа и обработки сигналов обычно имеет дело с сигналами в определенном интервале [a, b] их значений, при этом максимальной дифференциальной энтропией обладает равномерное распределение значений сигналов:
h(U) = -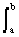
p(u) log p(u) du = log (b-a).
По мере сужения плотности распределения значение h(U) уменьшается, и в пределе при p(u)
® d(u-c), a<c<b стремится к нулю.Понятие же "физического вакуума" в релятивистской квантовой теории поля подразумевает, что во-первых, он не имеет физической природы, в нем лишь виртуальные частицы у которых нет физической системы отсчета, это "фантомы", во-вторых, "физический вакуум" - это наинизшее состояние поля, "нуль-точка", что противоречит реальным фактам, так как, на самом деле, вся энергия материи содержится в эфире и нет иной энергии и иного носителя полей и вещества кроме самого эфира.
В отличие от лукавого понятия "физический вакуум", как бы совместимого с релятивизмом, понятие "эфир" подразумевает наличие базового уровня всей физической материи, имеющего как собственную систему отсчета (обнаруживаемую экспериментально, например, через фоновое космичекое излучение, - тепловое излучение самого эфира), так и являющимся носителем 100% энергии вселенной, а не "нуль-точкой" или "остаточными", "нулевыми колебаниями пространства". Подробнее читайте в FAQ по эфирной физике.
|
|
 |