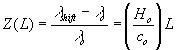
(1)
Kazan Physical-Technical Institute
Abstract.
A new interpretation of cosmological redshifts is proposed to construct the evolved-vacuum model of this phenomenon. The physical vacuum was considered to be a real matter with time-dependent permittivity and permeability. These parameters was shown on the base of Maxwell’s equations and Hubble’s law to obey the exponential behavior with a relative alteration of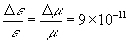 per year causing step-by-step decrease of light velocity with a rate of about 2.7 m/s over 100 years.
Cosmological aspects are discussed to explain some features of reality of the Universe evolution.
per year causing step-by-step decrease of light velocity with a rate of about 2.7 m/s over 100 years.
Cosmological aspects are discussed to explain some features of reality of the Universe evolution.
1. Introduction
It was experimentally established early in this century that the fainter distant galaxies and quasars are, the larger their shift of spectral lines toward the red region is. Assuming a plausible faintness-distance function, Hubble [1] discovered that there is a linear dependence between a fractional redshift and distance L
|
|
(1) |
In this relation, Z(L) is the relative spectral shift, λo is the wavelength of a spectral line from a source measured in a laboratory which is at rest relative to the Earth, λshift is the wavelength of the same line emitted by a quasar and measured by a terrestrial observer in the same laboratory, Ho is the Hubble constant and co is the free space velocity of light. Until now, such spectral observations yielding information about extremely distant objects were being the only experimental clues to support an understanding of the Universe. This is because only such gigantic distances (of about 1022 km) and time intervals (109 years) suffice to reveal the small changes that occur while light is traveling through space. Therefore, a correct interpretation of such spectral observations to ascertain the real origin of redshifts and bring the Universe to light is especially important.
At present, there are several alternative models to explain the redshift phenomenon. Usually, this one is interpreted as a Doppler effect which finally implies recession of galaxies and expansion of the Universe (the "Big Bang" model).There are some doubts, however, about this interpretation .Really, there is no physical explanation for singularities due to infinite density of matter at the point of creation, and some recession velocities appear to be extremely large. For example, for quasar Q01442+101 (at Z =3,3) the recession velocity derived from this model is about of 0.9co . Moreover, some super-clusters of galaxies seem to be older than the age of the Universe derived from this model. It was experimentally established recently that very extended objects (the huge sheets of galaxies stretching more than 200 million light-years (l.y.) across , 700 million l.y. long and 20 million l.y. thick ) are like the super-clusters of galaxies mapped by Tully earlier [2]. Still larger objects ("Cosmic Ladder") stretching across a distance of about seven billion light-years have been discovered [3]. Because the maximal velocities of any objects experimentally observed in astronomy to be not more than 500 km/s it takes about 150 billion years to form this structure – more than seven times the number of years since the Big Bang to form the Universe [3].
Besides the Big-Bang there are also alternative approaches based on ideas of time evolution of matter/light parameters, either the fundamental physical constants (Plank’s constant, charge and mass of elementary particles, the electromagnetic parameter co and so on) or the electromagnetic characteristics of the physical vacuum.
The variation of fundamental physical constants as a possible origin of the redshifts has been discussed widely since Dirac [4] put forward the idea of "Great Numbers". Recently, however, some of the atomic constants were really shown to be constant in time. For instance, Potekhin and Varshalovich [5] have studied the fine splitting of the doublet absorption lines in quasar’s spectra. They analyzed 1414 doublets (CIV, NV, CVI, MgII, AlIII, and SiIV) in the wide range of redshifts (0.2<Z<3.7). Their statistical analysis reveals no statistically significant time variation of the fine structure constant 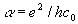 on time scale of about ten billion years. We can conclude from here that, at least, such the parameters as charge of electron e, Plank’s constant h and electromagnetic coefficient co should be considered as constant ones and, hence, can have no influence on redshifts. As for variation of the mass of elementary particles, this idea discussed by Arp [6] in the intrinsic-redshift model to prove that redshifts are supposedly related to the age of the objects. This idea, however, do not obey the redshift-distance relation (1) at constant Ho [7] . Moreover, constancy of the electron mass in time should follow from the results of [5] as well. Really, because the fine splitting of energy levels
δE is
on time scale of about ten billion years. We can conclude from here that, at least, such the parameters as charge of electron e, Plank’s constant h and electromagnetic coefficient co should be considered as constant ones and, hence, can have no influence on redshifts. As for variation of the mass of elementary particles, this idea discussed by Arp [6] in the intrinsic-redshift model to prove that redshifts are supposedly related to the age of the objects. This idea, however, do not obey the redshift-distance relation (1) at constant Ho [7] . Moreover, constancy of the electron mass in time should follow from the results of [5] as well. Really, because the fine splitting of energy levels
δE is
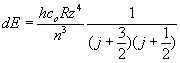
to depend on Ridberg’s constant 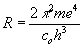 it follows from their statistical analysis that R is a constant in a very wide range 0.2<Z<3.7. In other words, we should conclude for the experimental test to show that electron mass m is also constant on a very large time scale.
it follows from their statistical analysis that R is a constant in a very wide range 0.2<Z<3.7. In other words, we should conclude for the experimental test to show that electron mass m is also constant on a very large time scale.
There are also alternative models of redshifts which obey the redshift-distance relation. This one is based on an idea of gradual alteration of light parameters due to interaction between light and matter while the light is traveling gigantic distances through space for a very long time. There are two candidate ways for such interaction to cause redshifts: gradual energy loss by the photon due to absorption during propagation of light with a constant velocity (tired-light model, see, for instance, [8]) and propagation of light with the variable velocity and without absorption in free space (variable-light-velocity models).
Tired-light mechanism, however, results in obvious contradictions between quantum and classical description based on the Maxwell’s equations. In fact, assuming that energy of a single photon is gradually decreasing due to absorption, we may conclude that volume energy density of N photon flow with this same frequency and, hence, its intensity are also decreasing ones. From the electrodynamics point of view, it means that electric field strength E should gradually be decreased while this wave is traveling through space . Quantum description says about simultaneous decreasing of frequency at decreasing of photon energy. However, it is not difficult to be convinced (see Appendix) that no such a combination, i.e. the simultaneous decaying space-dependent functions E(x) and ω(x) , obeys this same wave equation with stationary boundary conditions which is currently used in quantum electronics and physical optics to adequately describe the propagation of light at constant velocity in any non-conductors, including vacuum.
At present, vacuum has been experimentally established to be not a void but it is some material medium with definite but not so far investigated features. It was really confirmed by observation of several vacuum effects, for instance, zero oscillations and polarization of vacuum, generating the particles in vacuum due to electromagnetic interaction. Therefore, it was reasonable to assume that this real matter-physical vacuum can possess internal friction due to its small but a real viscosity to result in variation of light-matter interaction. That is, vacuum can affect on the light wave because of certain resistance. This may be a reason for the redshifts observed.
Because physical vacuum is a real material with real characteristics the light velocity can be non-constant, since it depends on both co , ε and μ of the vacuum all of which could have been space/time-dependent functions, in principle. The electromagnetic coefficient co, which bridges the electric and magnetic phenomena, has the dimension of speed, and has been historically identified with a constant free space light velocity. For example, the situation with space variable ε(x) and μ(x) at the constant electromagnetic parameter co was discussed in [9] where a wave equation with the term analogous to one for a damped simple oscillator was derived from Maxwell’s equations. Solution of this equation leads to a gradual increase of a wavelength ( redshifts at constancy of the frequency) and variable light velocity. A drawback of the last approach is what one needs to consider the permittivity and permeability rather as parameters of interaction but not just the characteristics of vacuum as real matter. This inconvenience was overcame in [10] where this same result was obtained, but at constant permittivity/permeability and the space-dependent electromagnetic parameter co. However, following the publication of the work [5] followed by conclusion about constancy of co the last model [10] must be obviously abandoned . In the present paper we will consider more promising variable light velocity model of redshifts which let us join electrodynamical approach with the cosmological principle and empirical data to be available in order to explain some features of reality.
2. Evolved-vacuum model (EVM) of cosmological redshifts
This model is based on classical electrodynamics with taking the time-dependent permittivity and permeability into account [11]. Let us make only one assumption that, in compliance with the cosmological principle, the variation of the physical vacuum parameters occurs simultaneously and identically at any point of the infinite evolving Universe. Then the permittivity and permeability of the physical vacuum at the moment when light is leaving a distant galaxy (one point of space) would be different from what it would be when this light is reaching the Earth (the other point of the Universe) to be a reason for shifts of spectral lines. Let us consider this point in more detail by writing Maxwell’s equations for the plane-polarized monochromatic wave propagating along the OX-axis at ε(t) and μ(t) as the functions of time
|
|
(2) |
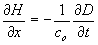
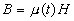
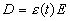
Consideration of the light wave as a plane one here is due to quasars removed on infinity are practically point sources of light with flat wave fronts near the Earth. The simplest way of analyzing the situation under these conditions is to write down a wave equation for the induction wave D instead of the electric field strength E. One can argue that wave characteristics of induction have the same phase behavior as for the electric field. However, solving the induction wave equation and then making use of the material relations in (2) to find the electric field strength is much simpler. The wave equation for induction can be derived from a chain of substitutions
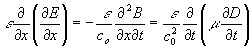
drawn from Eqs.2 by means of taking a partial derivative of the left part of the first equation with respect to x and using the second equation in (2). This leads to the wave equation for electric induction
|
|
(3) |
with the boundary and initial conditions :
at x =0 and t = ts ( ts is the start instant when the light left the remote source) the electric field strength in the wave zone is E(0,ts)= Eoexp ω
where the amplitude and frequency are constant, and
D(0,ts) = ε(ts)E(0,ts)
One can see from (3) that the vacuum propagation velocity of the induction wave is a time-dependent function
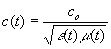
and this must be the same as the light velocity.
Let us seek a solution of Eq.3 as a quasi-periodic function with variable phase
|
|
(4) |
The induction is an electric field strength in a void, i.e. in a space without any matter (including physical vacuum) filling it. Because there is no field-matter interaction in the void the amplitude of induction in (4) can be considered as a constant. Differentiating (4), inserting into (3) and separating real and imaginary parts, we obtain two equations
|
|
(5) |
where 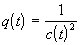 and
and 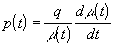
In order to admit time dependence for both permeability and permittivity, we should repeat the same analysis for the magnetic induction wave equation. Following the differentiating of the left side of the second equation (2) with respect to x and making the necessary substitutions using the first one we obtain the same equation as Eq.(3) but with B in place of D and ε in place of μ in the bracket in the third term. Obviously, the solution is
formally the same as Eqs.(5), but with ε in place of μ in the definition
of p(t). Using this conclusion p(t,ε) = p(t,μ) and the definition
of  , we obtain
, we obtain
|
|
(6) |
where Q is either an as-yet unknown function on time or a constant to be found later. Taking it into account we can rewrite the Eqs. (5) as follows
|
|
(7) |
It is seen from (6) that the behavior of the light velocity is the same as permeability and permittivity time behavior at any point of space (in compliance with the cosmological principle as well).This means that an observer at any concrete space point on the light path sees the wave as a periodic function whose period depends on the light velocity at this epoch. In other words, the light frequency perceived by the observer depends on time alone. Thus, the right part of the first equation (7), which keeps the frequency 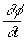 and light velocity, depends only on time. Therefore, let us seek the phase of the light in the form φ (x,t) = ζ (t) η (x). Inserting this form into the first equation (7), we derive
and light velocity, depends only on time. Therefore, let us seek the phase of the light in the form φ (x,t) = ζ (t) η (x). Inserting this form into the first equation (7), we derive
|
|
(8) |
Since η (x) depends only on space and ζ (t) depends only on time, the parameter k must be constant. It follows from solving the Eq.8 that η(x) is a linear function of x , that is η(x) = ±kx + φo . It is easy to show that this form will also obey the second of Eqs.(7). Thus the parameter k is a spatial derivative of phase, or a spatial frequency, i .e. a well-known wave number 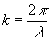 .
.
Thus we have for phase
|
|
(9) |
Thus we come to a very important conclusion: the induction wave, and hence the light one, must travel in vacuum with conservation of wave length even when the parameters of vacuum are time dependent. This wavelength is determined by the initial and boundary conditions (at the point near a quasar location at the moment of start of the light wave ,i.e. when light is leaving the quasar)
|
|
(10) |
where ts is the start instant, when light left the source, c(ts) - the velocity of light at the concrete epoch of the Universe evolution and ω(ts)=ωo is the frequency of the atomic transition of the atom in question,. The time dependent frequency ω(t) = ¶φ/¶t can be inferred from (9), given c(t) , which can in turn be inferred from (6), given Q(t). To determine Q(t) let us refer to the redshift-distance relation (1). The distance covered by light depends both on ts (the start moment) and to(the observation time -our epoch at the Earth) and can be written as follows
|
|
(11) |
Taking this into account, we can rewrite the relation (1) in the form
|
|
(12) |
where initial conditions for the wave lengths of light are (10) for a remote source (at ts) and (13) for a terrestrial source (at our epoch )
|
|
(13) |
In the relation (12) the light velocity c
|
|
(14) |
This result is in accord with the Eqs.6 derived from the wave equation with parameter Q set to minus the Hubble’s constant Ho , i.e. at Q=-Ho.
Solving these equations in the range ts < t < to with our initial conditions, we obtain an exponential law of time variation of the light velocity, permittivity and permeability of vacuum:
|
|
(15) |
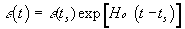
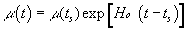
Using (15) in (8) with the initial condition (10) and k =2π/λ(ts) , we obtain the time-dependent part of the phase for the time range of ts < t <to as follows
|
|
(16) |
Because the time derivative of this phase is the frequency of the light wave we obtain the same behavior for frequency measured by the observer as for light velocity in the same time range
|
|
(17) |
Thus the induction wave, which is traveling through space, has constant amplitude and the constant wavelength, causing an optical detector to register the variable frequency due to gradual time variation of the vacuum parameters . The behavior of the electric field strength can be derived from the last material relation in (2) with taking into account (4), (15) and the initial conditions in (3) as follows
|
|
(18) |
where the amplitude of the electric field is seen to decline with time, and the phase is
|
|
(19) |
We may use expressions (17), (18) and (19) for any source in space in dependence on situation. For instance, in order to compare the parameters of light arrived on the Earth with ones measured for terrestrial source at the same instant to (our epoch) we should put t = to in (15), (17). As a result we have the following.
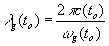
Where the light velocity at our epoch is c (to) = co. The frequency of this light perceived by an observer is 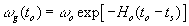 (from Ex.17 at t = to)
(from Ex.17 at t = to)
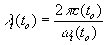 where the frequency of this source is ωt(to)=ωo (from Ex.18 at t = to = ts ,because there is practically no time interval between emitting and observing the terrestrial source wave)
where the frequency of this source is ωt(to)=ωo (from Ex.18 at t = to = ts ,because there is practically no time interval between emitting and observing the terrestrial source wave) 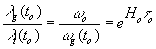
where a look-back time 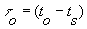
Thus, in compliance with experiment, there is the redshift
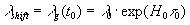
Although reproducing the conclusions of the tired-light model, namely, about simultaneous decreasing the electric field strength and frequency, this model has a different physical interpretation. Instead of energy loss due to absorption at constant light velocity, this mechanism is based on gradual change of the vacuum parameters that results in declining of the electric field strength. The electromagnetic wave is gradually slowing down, with conservation of the initially shifted wavelength λshift. The frequency perceived by observers at any point on the light path depends on the light velocity being at the observation time.
3. Cosmological aspects
The cosmological principle implies that the Eqs.15 derived for the interval τo = to - ts can be extrapolated from present observation time to to any future or past one. If we take our epoch as zero point on the time scale the light velocity in the Exp.15 can be rewritten as follows
|
|
(20) |
where t<to serves to define history of the Universe before our epoch. For t>to we have future of the Universe. The exponential dependence implies no particular points or singularities on the time axis. That is, all of the variations of the Universe parameters have neither beginning nor end but occur always and everywhere, identically. Such variation is very small (for instance, as follows from Ex.20 at co =3 108m/s and Ho =100kms-1Mpc-1 , i.e. 2,9 10-18s-1 , it is about of 2.7 m/s for the interval of 100 years). However it is quite measurable with contemporary techniques. Recently, Montgomery and Dolphin [12] performed a statistical analysis of extensive experimental data to argue that light velocity is variable in time. This analysis shows the measured value of light velocity to have decreased slightly over the past 250 years. Such behavior of the light velocity can permit a steady-state cosmology with the boundless Universe that has always existed, and is homogeneous on the very large scale. Making use of (11) with (15), we can find the distance r covered by light for any moment of time after the start time when the light left the quasar
|
|
(21) |
Unlike the constant light-velocity model, this model says that the distance approaches a certain limit in a certain interval of time 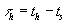 . At, the τ h ~=(5 ± 6)/Ho the distance reaches the limit
. At, the τ h ~=(5 ± 6)/Ho the distance reaches the limit
|
|
(22) |
This limit distance is due to total declining the electric field strength (19) and can be interpreted as a spatial cosmological horizon for light. If we take this horizon into account the photometric Olbers’ paradox [13] has a natural explanation. Indeed, the light from a galaxy cluster cannot possibly reach the Earth if the Earth is situated beyond the light horizon that is available for this cluster. In other words, a terrestrial observer can see only some remote clusters the horizons of which are in excess of the look-back time τo = to - ts, i.e. for τo<τh . It is interesting that the earlier light has been emitted, the larger its horizon is, because of larger light velocity at this moment of start. Hence the light horizon for quasars associated with the younger Universe is larger than that for more recent ones. Using (20) at t = ts and (21) at t = to in (1) where L = L (τo) = r (to) we obtain the relative shift
|
|
(23) |
It follows from evaluation in (23) that the maximal Z, being for the horizon (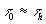 ), is in the range of about 150-500. However, no empirical Z measured up to now exceeds 5. If we take a real declining of light intensity into account this can be explained in the following way. In reality, we have a spherical wave front from the point source (remote galaxy) intensity of which is as the inverse square of the distance. In fact, the relation
), is in the range of about 150-500. However, no empirical Z measured up to now exceeds 5. If we take a real declining of light intensity into account this can be explained in the following way. In reality, we have a spherical wave front from the point source (remote galaxy) intensity of which is as the inverse square of the distance. In fact, the relation
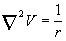
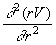
is valid for any function V(r) where the radius of a spherical wave is 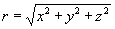 (see, for instance, [14]). Therefore, we may place the product (rD) instead of D into the Eq.3 without changing of it (at the same directions of the light beam r and x). Thus, we obtain the induction in a wave zone (r>>λ/2ω ) as a spherical wave and, hence, the electric field strength has a form
(see, for instance, [14]). Therefore, we may place the product (rD) instead of D into the Eq.3 without changing of it (at the same directions of the light beam r and x). Thus, we obtain the induction in a wave zone (r>>λ/2ω ) as a spherical wave and, hence, the electric field strength has a form
|
|
(24) |
where φ(x,t) is the phase in (19). The intensity of this wave is
|
|
(25) |
In order to estimate decreasing intensity with distance and look-back time let us use of (15) and (21) at t = to with inserting the parameters of our epoch c(to), ε(to) and L(τo)= r(to) into (25). Following the substitutions we have
|
|
(26) |
where 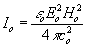 .
.
Let us compare this one with the intensity of this wave taken at some previous point of optical path from the source 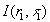 where
where 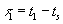 and
and 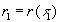 .
The distance
.
The distance 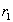 is chosen much shorter than L(τo) but long enough to consider the galaxy as a point source.
is chosen much shorter than L(τo) but long enough to consider the galaxy as a point source.
With aim to compare this we derive the relation 
|
|
(27) |
where we have taken 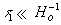 into account at series expansion of the exponent. According to current data, the Hubble’s constant is in the range of 60-140kms-1Mpc-1. Making use of Ho =100kms-1Mpc
into account at series expansion of the exponent. According to current data, the Hubble’s constant is in the range of 60-140kms-1Mpc-1. Making use of Ho =100kms-1Mpc
Table 1
|
τo (look-back time) |
Z (redshift) |
β (at variable c) |
β c(at constant c) |
|
Ho-1 = 1.08 1010years |
1.8 |
1.5 10-11 |
2 10-7 |
|
2Ho-1 |
6.8 |
1.2 10-13 |
5 10-8 |
|
3Ho-1 |
21 |
2.1 10-15 |
2.2 10-8 |
|
4Ho-1 |
60 |
3 10-17 |
1.2 10-8 |
|
5Ho-1 |
170 |
4.5 10-19 |
8 10-9 |
|
6Ho-1 |
480 |
7 10-21 |
5 10-9 |
|
|
|
|
|
It is seen from here that intensity of light is falling more abruptly in the case of the variable light velocity compared to the constant light velocity model. This appears to result in very strong restriction of the visible horizon to make measuring of Z more than 6 practically impossible at sensitivity of up-to-day equipment. Really, the quasar with the most redshift (Z= 5) have been observed recently with Subaru Telescope.
4. Conclusion
A new model of cosmological redshifts developed on the base of classical electrodynamics and experimental Hubble’s law is discussed in this paper. In distinction from the usual wave equation the modified one (3) obtained here has the third term taking into consideration interaction the light with physical vacuum as a real matter. The light was concluded from solving this equation to propagate in vacuum with a constant wavelength being initially (10) and variable velocity (15) caused by gradual changing of permittivity and permeability of physical vacuum in time (at a relative rate of about 10-10 per year).Actually, for very long time while the light is traveling in space from a quasar to the Earth conserving its wavelength, the wavelength of a terrestrial source is being changed due to evolution of the Universe resulting in fractional blueshift compared to the light arrived from the remote quasar, i.e. we observe as if the redshift for the line of the remote source. For this same reason the frequency of the traveling light perceived by the observer on the Earth is a function of time (17 ) to be different from the frequency ωo specified by the energy transition which remains constant in time at any point of the Universe for any atom in question. In distinction from the tired-light model, decreasing of the amplitude of the electric field strength (18) during the travel through space is due to not absorption. From this EVM such a behavior is a result of time evolution of physical vacuum. This model offers novel explanations not only for the redshift origin but also for several other observed features of reality, for instance, Olber’s paradox and limitation of Z.
5. Appendix
To study the propagation of light at constant velocity in any non-conductors, including vacuum consider the usual wave equation [14] with stationary boundary conditions
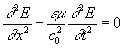 (1A)
(1A)
at E(0,t)= Eoexp ωot и 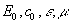 - constant
- constant
In order to discuss the tired-light model let us seek a solution of this equation as a quasi-periodic function with variable phase and x-dependent amplitude
 (2A)
(2A)
Inserting this into the equation and separating real and imaginary parts we obtain two following equations
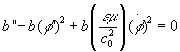 (3A)
(3A)
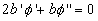
where 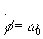 = const.
= const.
Taking it into account that 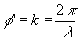 the second equation in (3A) can be rewritten as follows
the second equation in (3A) can be rewritten as follows
2b'λ-bλ'=0 (4A)
It follows from here the condition
b/λ=2b'/λ'. (5A)
Because the left hand side is always positive one the x- derivative signs for b and λ should be this same. It means that the light should have either redshift (at λ'>0) with increasing of the amplitude (at 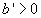 , that is absurd!) or blueshift (at λ'<0 which is no compliance with experiments) with decreasing amplitude (at
, that is absurd!) or blueshift (at λ'<0 which is no compliance with experiments) with decreasing amplitude (at  ).
).
Thus the situation with the different x- derivative signs required by tired-light model (λ'>0 with b'<0) is not acceptable for the usual wave equation with stationary conditions which is widely used in quantum electronics and physical optics to adequately describe the propagation of light at constant velocity in any medium ,including vacuum .
References
[1] E.P.Hubble, Proc. Nat. Acad. Sci. 15, 168 (1929).
[2] R.Brent Tully, Astrophysical Journal,303,25(1986).
R.Brent Tully, J.R.Fisher, Atlas of Nearby Galaxies,(Cambridge: Cambridge University Press,1987)
[3] E.J.Lerner, The Big Bang never happened,(Simon & Schuster Ltd,London,1992).
[4] P.A.M. Dirac, Nature 139,323 (1937).
[5] A. Potekhin, D.Varshalovich, Astronomy and Astrophysics Supplement 104,89 (1994).
[6] H. Arp, Progress in New Cosmologies,(Plenum Press, New York,1,1993).
[7] H.Arp, Quasars, Redshifts and Controversies, Interstellar Media, (Berkeley,1987).
[8] L.De Broglie,Cahiers de Physique,16,425 (1962).
[9] E.I.Shtyrkov,Gal.Electrodynamics,3,66 (1992).
[10] E.I.Shtyrkov,Progress in New Cosmologies, Plenum Press, New York,327 (1993).
[11] E.I.Shtyrkov,Gal. Electrodynamics,8,3,57 (1997).
[12] A.Montgomery,L.Dolphin,Gal.Electrodynamics 5,93 (1993).
[13] H.W.M.Olbers,Edinburg New Philosophical Journal,1,141 (1826).
[14] M.Born,E.Wolf,Principles of optics,(Pergamon Press,New York,1964)
|
|