
Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при определенных условиях при наложении двух или нескольких световых пучков. Интенсивность света в области перекрытия пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков.
При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света. Первый эксперимент по наблюдение интерференции света в лабораторных условиях принадлежит Роберту Гуку (1660). Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 1). Интерференционная картина имела вид концентрических колец, получивших название "колец Ньютона", так как Исаак Ньютон присвоил это открытие себе и множество его апологетов размножило этот акт плагиата как истинно ньютоновское открытие. (рис. 2).
 |
| Рисунок 1. Наблюдение колец Ньютона. Интерференция возникает при сложении волн, отразившихся от двух сторон воздушной прослойки. «Лучи» 1 и 2 – направления распространения волн; h – толщина воздушного зазора. |
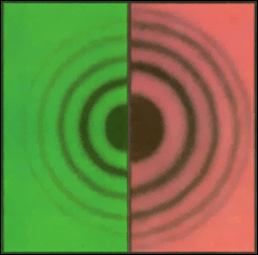 |
| Рисунок 2. Кольца Ньютона (Гука) в зеленом и красном свете. |
Ньютон не смог объяснить с точки зрения корпускулярной теории, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов. Исторически первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2 (рис. 3). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
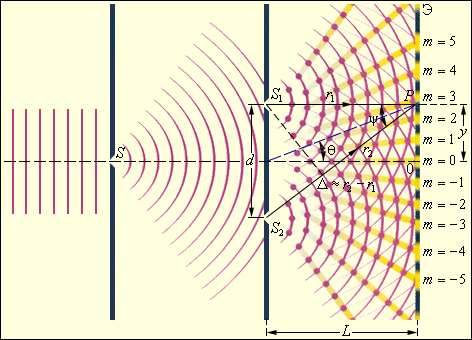 |
| Рисунок 3. Схема интерференционного опыта Юнга. |
Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S1 и S2, которые можно рассматривать в соответствии с принципом Гюйгенса как источники вторичных волн, освещались светом одного источника S.
При симметричном расположении щелей вторичные волны, испускаемые источниками
S1 и S2, находятся в фазе, но эти волны проходят до точки наблюдения P разные
расстояния r1 и r2. Следовательно, фазы колебаний, создаваемых волнами от
источников S1 и S2 в точке P, вообще говоря, различны. Таким образом, задача об
интерференции волн сводится к задаче о сложении колебаний одной и той же
частоты, но с разными фазами. Утверждение о том, что волны от источников S1 и S2
распространяются независимо друг от друга, а в точке наблюдения они просто
складываются, является опытным фактом и носит название принципа
суперпозиции. Монохроматическая волна, распространяющаяся в
направлении радиус-вектора 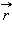 , записывается в виде
, записывается в виде
| E = a cos (ωt – kr), |
где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ:
| E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ). |
Не существует приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2. Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:
|
(*) |
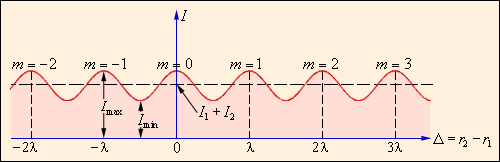
где Δ = r2 – r1 – так называемая разность хода. Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2, ...). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивности Imin = (a1 – a2)2 < I1 + I2. На рис. 4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.
 4 4 |
| Рисунок 4. Распределение интенсивности в интерференционной картине. Целое число m – порядок интерференционного максимума. |
В частности, если I1 = I2 = I0, то есть интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид:
|
|
(**) |
В этом случае Imax = 4I0, Imin = 0. Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты. Различие проявляются только в том, как зависит разность хода Δ от положения точки наблюдения P. Если в схеме Юнга через y обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда d << L и y << L (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить:
 |
При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl, то есть при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно,
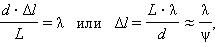 |
где ψ – угол схождения «лучей» в точке наблюдения P. Выполним количественную оценку. Допустим, что расстояние d между щелями S1 и S2 равно 1 мм, а расстояние от щелей до экрана Э составляет L = 1 м, тогда ψ = d / L = 0,001 рад. Для зеленого света (λ = 500 нм) получим Δl = λ / ψ = 5 · 105 нм = 0,5 мм. Для красного света (λ = 600 нм) Δl = 0,6 мм. Таким путем Юнг впервые измерил длины световых волн, хотя точность этих измерений была невелика.
Следует подчеркнуть, что в волновой оптике, в отличие от геометрической оптики, понятие луча света утрачивает физический смысл. Термин «луч» употребляется здесь для краткости для обозначения направления распространения волны. В дальнейшем этот термин будет употребляться без кавычек. В эксперименте Гука (рис. 1) при нормальном падении волны на плоскую поверхность линзы разность хода приблизительно равна удвоенной толщине 2h воздушного промежутка между линзой и плоскостью. Для случая, когда радиус кривизны R линзы велик по сравнению с h, можно приближенно получить:
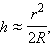 |
где r – смещение от оси симметрии. При написании выражения для разности хода следует также учесть, что волны 1 и 2 отражаются при разных условиях. Первая волна отражается от границы стекло–воздух, а вторая – от границы воздух–стекло. Во втором случае происходит изменение фазы колебаний отраженной волны на π, что эквивалентно увеличению разности хода на λ / 2. Поэтому
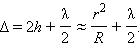 |
При r = 0, то есть в центре (точка соприкосновения) Δ = λ / 2; поэтому в центре колец Гука всегда наблюдается интерференционный минимум – темное пятно. Радиусы rm последующих темных колец определяются выражением
|
Эта формула позволяет экспериментально определить длину волны света λ, если известен радиус кривизны R линзы. Проблема когерентности волн. Теория Юнга позволила объяснить интерференционные явления, возникающие при сложении двух монохроматических волн одной и той же частоты. Однако повседневный опыт учит, что интерференцию света в действительности наблюдать не просто. Если в комнате горят две одинаковые лампочки, то в любой точке складываются интенсивности света и никакой интерференции не наблюдается. Возникает вопрос, в каких случаях нужно складывать напряженности (с учетом фазовых соотношений), и в каких случаях нужно складывать интенсивности волн, то есть квадраты напряженностей полей? Теория интерференции монохроматических волн не может дать ответа на этот вопрос.
Реальные световые волны не являются строго монохроматическими. В силу фундаментальных физических причин излучение всегда имеет статистический характер. Атомы светового источника излучают независимо друг от друга в случайные моменты времени, и излучение каждого атома длится очень короткое время (τ ≤ 10–8 с). Результирующее излучение источника в каждый момент времени состоит из вкладов огромного числа атомов. Через время порядка τ вся совокупность излучающих атомов обновляется.
Поэтому суммарное излучение будет иметь другую амплитуду и, что особенно важно, другую фазу. Фаза волны, излучаемой реальным источником света, остается приблизительно постоянной только на интервалах времени порядка τ. Отдельные «обрывки» излучения длительности τ называются цугами. Цуги имеют пространственную длину, равную cτ, где c – скорость света. Колебания в разных цугах не согласованы между собой.
Таким образом, реальная световая волна представляет собой последовательность волновых цугов с беспорядочно меняющейся фазой. Принято говорить, что колебания в разных цугах некогерентны. Интервал времени τ, в течении которого фаза колебаний остается приблизительно постоянной, называют временем когерентности.
Интерференция может возникнуть только при сложении когерентных колебаний, то есть колебаний, относящихся к одному и тому же цугу. Хотя фазы каждого из этих колебаний также подвержены случайным изменениям во времени, но эти изменения одинаковы, поэтому разность фаз когерентных колебаний остается постоянной. В этом случае наблюдается устойчивая интерференционная картина и, следовательно, выполняется принцип суперпозиции полей.
При сложении некогерентных колебаний разность фаз оказывается случайной функцией времени. Интерференционные полосы испытывают беспорядочные перемещения из стороны в сторону, и за время Δt их регистрации, которая в оптических экспериментах значительно больше времени когерентности (Δt >> τ), происходит полное усреднение. Регистрирующее устройство (глаз, фотопластинка, фотоэлемент) зафиксирует в точке наблюдения усредненное значение интенсивности, равное сумме интенсивностей I1 + I2 обоих колебаний. В этом случае выполняется закон сложения интенсивностей.
Таким образом, интерференция может возникнуть только при сложении когерентных колебаний. Волны, создающие в точке наблюдения когерентные колебания, также называются когерентными. Волны от двух независимых источников некогерентны и не могут дать интерференции. Т. Юнг интуитивно угадал, что для получения интерференции света нужно волну от источника разделить на две когерентные волны и затем наблюдать на экране результат их сложения. Так делается во всех интерференционных схемах. Однако, даже в этом случае интерференционная картина исчезает, если разность хода Δ превысит длину когерентности cτ.
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|