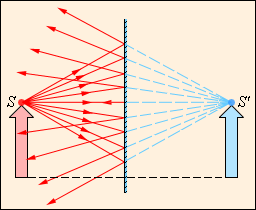
Простейшим оптическим устройством, способным создавать изображение предмета, является плоское зеркало. Изображение предмета, даваемое плоским зеркалом, формируется за счет лучей, отраженных от зеркальной поверхности. Это изображение является мнимым, так как оно образуется пересечением не самих отраженных лучей, а их продолжений в «зазеркалье» (рис 1).
|
| Рисунок 1. Ход лучей при отражении от плоского зеркала. Точка S' является мнимым изображением точки S. |
Вследствие закона отражения света мнимое изображение предмета располагается симметрично относительно зеркальной поверхности. Размер изображения равен размеру самого предмета. Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента. Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом.
Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала. Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом зеркала F. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала (рис 2).
 |
| Рисунок 2. Отражение параллельного пучка лучей от вогнутого сферического зеркала. Точки O – оптический центр, P – полюс, F – главный фокус зеркала; OP – главная оптическая ось, R – радиус кривизны зеркала. |
Следует иметь в виду, что отраженные лучи пересекаются приблизительно в одной точке только в том случае, если падающий параллельный пучок был достаточно узким (так называемый параксиальный пучок). Главный фокус выпуклого зеркала является мнимым. Если на выпуклое зеркало падает пучок лучей, параллельных главной оптической оси, то после отражения в фокусе пересекутся не сами лучи, а их продолжения (рис 3).
 |
| Рисунок 3. Отражение параллельного пучка лучей от выпуклого зеркала. F – мнимый фокус зеркала, O – оптический центр; OP – главная оптическая ось. |
Фокусным расстояниям сферических зеркал приписывается определенный знак: для
вогнутого зеркала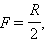 
для выпуклого 
где R – радиус кривизны зеркала.
Изображение какой-либо точки A предмета в сферическом зеркале можно построить с
помощью любой пары стандартных лучей:
На рис 4 перечисленные выше стандартные лучи изображены для случая вогнутого зеркала. Все эти лучи проходят через точку A', которая является изображением точки A. Все остальные отраженные лучи также проходят через точку A'. Ход лучей, при котором все лучи, вышедшие из одной точки, собираются в другой точке, называется стигматическим. Отрезок A'B' является изображением предмета AB. Аналогичны построения для случая выпуклого зеркала.
 |
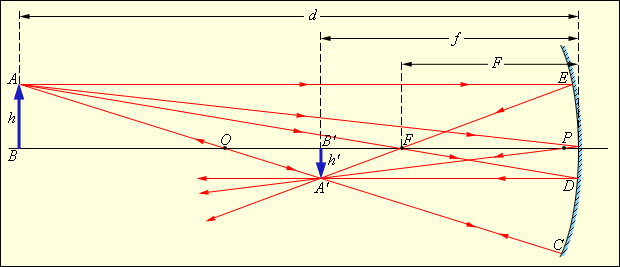| Рисунок 4. Построение изображения в вогнутом сферическом зеркале. |
Положение изображения и его размер можно также определить с помощью формулы сферического зеркала:
|
Здесь d – расстояние от предмета до зеркала, f – расстояние от зеркала
до изображения. Величины d и f подчиняются определенному правилу знаков:
d > 0 и f > 0 – для действительных предметов и
изображений;
d < 0 и f < 0 – для мнимых предметов
и изображений. Для случая, изображенного на рис 4, имеем:
F > 0 (зеркало вогнутое); d = 3F > 0
(действительный предмет). По формуле сферического зеркала получаем: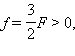 
следовательно,
изображение действительное. Если бы на месте вогнутого зеркала стояло выпуклое
зеркало с тем же по модулю фокусным расстоянием, мы получили бы следующий
результат: F < 0, d = –3F > 0,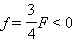 
– изображение
мнимое. Линейное увеличение сферического зеркала Γ определяется как отношение
линейных размеров изображения h' и предмета h. Величине h' удобно приписывать
определенный знак в зависимости от того, является изображение прямым
(h' > 0) или перевернутым (h' < 0). Величина h всегда
считается положительной. При таком определении линейное увеличение сферического
зеркала выражается формулой, которую можно легко получить из рис 4:
|
В первом из рассмотренных выше примеров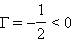 
– следовательно, изображение
перевернутое, уменьшенное в 2 раза. Во втором примере 
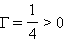– изображение прямое, уменьшенное в 4
раза.
|
|
 |
