Простейшей моделью молекулярно-кинетической теории является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур.
Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, газ, температура). В результате каждого столкновения между молекулами и молекул со стенкой скорости молекул могут изменяться по модулю и по направлению; на интервалах между последовательными столкновениями молекулы движутся равномерно и прямолинейно.
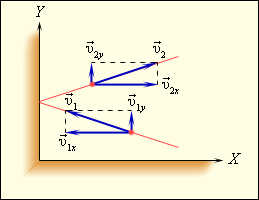
В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, то есть подчиняются законам классической механики. Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону динамики. В результате проекция vx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция vy скорости, параллельная стенке, остается неизменной (рис. 1).
 |
| Рисунок 1. Упругое столкновение молекулы со стенкой. |
Поэтому изменение импульса молекулы будет равно 2movx, где mo – масса молекулы. Выделим на стенке некоторую площадку S (рис. 2). За время Δt с этой площадкой столкнутся все молекулы, имеющие проекцию скорости vx, направленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой vxΔt.
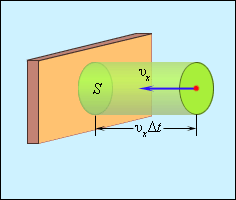 |
| Рисунок 2. Определение числа столкновений молекул с площадкой S. |
Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в
объеме цилиндра равно nSvxΔt. Но из этого числа лишь половина движется в сторону
стенки, а другая половина движется в противоположном направлении и со стенкой не
сталкивается. Следовательно, число ударов молекул о площадку S за время Δt равно
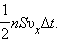 Поскольку каждая молекула при
столкновении со стенкой изменяет свой импульс на величину 2m0vx, то полное
изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно
Поскольку каждая молекула при
столкновении со стенкой изменяет свой импульс на величину 2m0vx, то полное
изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно
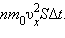 По законам механики это изменение
импульса всех столкнувшихся со стенкой молекул происходит под действием импульса
силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны
стенки на площадке S. Но по 3-му закону динамики такая же по модулю сила
действует со стороны молекул на площадку S. Поэтому можно записать:
По законам механики это изменение
импульса всех столкнувшихся со стенкой молекул происходит под действием импульса
силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны
стенки на площадке S. Но по 3-му закону динамики такая же по модулю сила
действует со стороны молекул на площадку S. Поэтому можно записать:
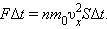 |
Разделив обе части на SΔt, получим:
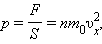 |
где p – давление газа на стенку сосуда. При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось X. На самом деле это не так. В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям.
Распределение молекул газа по модулю скоростей называется распределением Максвелла (1860 г.). Дж. К. Максвелл вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. На рис. 3 представлены типичные кривые распределения молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат – относительное число молекул, скорости которых лежат в интервале от v до v + Δv. Это число равно площади выделенного на рис. 3 столбика.
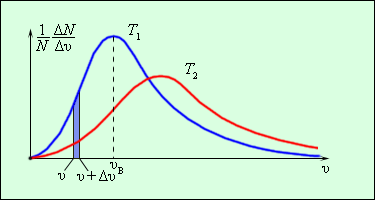 |
| Рисунок 3. Распределение молекул по скоростям. T2 > T1. |
Характерными параметрами распределения Максвелла являются наиболее
вероятная скорость vв, соответствующая максимуму кривой распределения, и
среднеквадратичная скорость 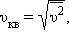 где
где 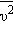 – среднее значение квадрата скорости.
С ростом температуры максимум кривой распределения смещается в сторону больших
скоростей, при этом vв и vкв увеличиваются. Чтобы уточнить формулу для давления
газа на стенку сосуда, предположим, что все молекулы, содержащиеся в единице
объема, разбиты на группы, содержащие n1, n2, n3 и т. д. молекул с
проекциями скоростей vx1, vx2, vx3 и т. д. соответственно. При этом
– среднее значение квадрата скорости.
С ростом температуры максимум кривой распределения смещается в сторону больших
скоростей, при этом vв и vкв увеличиваются. Чтобы уточнить формулу для давления
газа на стенку сосуда, предположим, что все молекулы, содержащиеся в единице
объема, разбиты на группы, содержащие n1, n2, n3 и т. д. молекул с
проекциями скоростей vx1, vx2, vx3 и т. д. соответственно. При этом
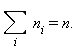 Каждая группа молекул вносит свой
вклад
Каждая группа молекул вносит свой
вклад 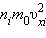 в давление газа. В результате
соударений со стенкой молекул с различными значениями проекций vxi скоростей
возникает суммарное давление
в давление газа. В результате
соударений со стенкой молекул с различными значениями проекций vxi скоростей
возникает суммарное давление
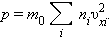 |
Входящая в это выражение сумма – это сумма квадратов проекций vx всех
n молекул в единичном объеме газа. Если эту сумму разделить на n, то мы получим
среднее значение 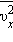 квадрата проекции
квадрата проекции 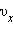 скорости молекул:
скорости молекул:
 |
Теперь формулу для давления газа можно записать в виде
|
Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой:
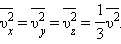 |
Последнее равенство вытекает из формулы:  Формула для среднего давления газа на
стенку сосуда запишется в виде
Формула для среднего давления газа на
стенку сосуда запишется в виде
|
Это уравнение устанавливает связь между давлением p идеального газа,
массой молекулы mo, концентрацией молекул n, средним значением квадрата скорости
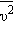 и средней кинетической энергией
и средней кинетической энергией 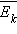 поступательного движения молекул. Его
называют основным уравнением молекулярно-кинетической теории газов. Таким
образом, давление газа равно двум третям средней кинетической энергии
поступательного движения молекул, содержащихся в единице объема. В основное
уравнение молекулярно-кинетической теории газов входит произведение концентрации
молекул n на среднюю кинетическую энергию
поступательного движения молекул. Его
называют основным уравнением молекулярно-кинетической теории газов. Таким
образом, давление газа равно двум третям средней кинетической энергии
поступательного движения молекул, содержащихся в единице объема. В основное
уравнение молекулярно-кинетической теории газов входит произведение концентрации
молекул n на среднюю кинетическую энергию 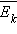 поступательного движения. Если
предположить, что газ находится в сосуде неизменного объема V, то
поступательного движения. Если
предположить, что газ находится в сосуде неизменного объема V, то 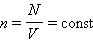 (N – число молекул в сосуде). В этом
случае изменение давления Δp пропорционально изменению
(N – число молекул в сосуде). В этом
случае изменение давления Δp пропорционально изменению 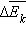 средней кинетической энергии.
Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую
энергию движения молекул в сосуде неизменного объема? Какую физическую величину
нужно изменить, чтобы изменилась средняя кинетическая энергия
средней кинетической энергии.
Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую
энергию движения молекул в сосуде неизменного объема? Какую физическую величину
нужно изменить, чтобы изменилась средняя кинетическая энергия 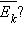
Такой величиной в физике является температура. Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты. Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.
Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).
Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С. В ряде стран (США) широко используется шкала Фаренгейта (TF), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно,
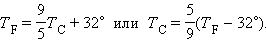 |
Особое место в физике занимают газовые термометры (рис. 4), в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (V = const), а термометрической величиной – давление газа p. Опыт показывает, что давление газа (при V = const) растет с ростом температуры, измеренной по шкале Цельсия.
 |
| Рисунок 4. Газовый термометр с постоянным объемом. |
Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки po и p100 на график, а затем провести между ними прямую линию (рис. 5). Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления. Экстраполируя график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна –273,15 °С и не зависит от свойств газа. Невозможно на опыте получить путем охлаждения газ в состоянии с нулевым давлением, так как при очень низких температурах все газы переходят в жидкие или твердые состояния.
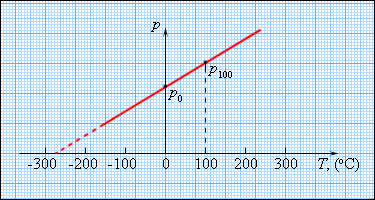 |
| Рисунок 5. Зависимость давления газа от температуры при V = const. |
Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:
| TK = TC + 273,15. |
В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой К. Например, комнатная температура TС = 20 °С по шкале Кельвина равна TK = 293,15 К. Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий. Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при нормальном атмосферном давлении, как это принято в шкале Цельсия. Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры, достаточно принять еще одну фиксированную опорную точку.
В шкале Кельвина в качестве такой точки используется температура тройной точки воды (0,01 °С), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273,16 К. Газовые термометры громоздки и неудобны для практического применения: они используются в качестве прецизионного стандарта для калибровки других термометров. Таким образом, давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре: p ~ T. С другой стороны, опыт показывает, что при неизменных объеме V и температуре T давление газа изменяется прямо пропорционально отношению количества вещества ν в данном сосуде к объему V сосуда
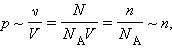 |
где N – число молекул в сосуде, NА – постоянная Авогадро, n = N / V – концентрация молекул (то есть число молекул в единице объема сосуда). Объединяя эти соотношения пропорциональности, можно записать:
|
где k – некоторая универсальная для всех газов постоянная величина. Ее называют постоянной Больцмана, в честь австрийского физика Людвига Больцмана (1844–1906), одного из создателей молекулярно-кинетической теории. Постоянная Больцмана – одна из фундаментальных физических констант. Ее численное значение в СИ равно:
| k = 1,38·10–23 Дж/К. |
Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить:
|
Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре. Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул. Следует обратить внимание на то, что средняя кинетическая энергия поступательного движения молекулы не зависит от ее массы. Броуновская частица, взвешенная в жидкости или газе, обладает такой же средней кинетической энергией, как и отдельная молекула, масса которой на много порядков меньше массы броуновской частицы. Этот вывод распространяется и на случай, когда в сосуде находится смесь химически невзаимодействующих газов, молекулы которых имеют разные массы. В состоянии равновесия молекулы разных газов будут иметь одинаковые средние кинетические энергии теплового движения, определяемые только температурой смеси. Давление смеси газов на стенки сосуда будет складываться из парциальных давлений каждого газа:
|
В этом соотношении n1, n2, n3, … – концентрации молекул различных газов в смеси. Это соотношение выражает на языке молекулярно-кинетической теории экспериментально установленный в начале XIX столетия закон Дальтона: давление в смеси химически невзаимодействующих газов равно сумме их парциальных давлений.
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|