В технике и окружающем нас мире часто приходится сталкиваться с процессами, которые называют колебательными.
Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.
Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения.
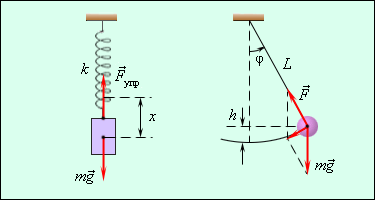
Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис. 1).
 |
| Рисунок 1. Механические колебательные системы. |
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными. Простейшим видом колебательного процесса являются гармонические колебания.
|
Здесь x - смещение тела от положения равновесия, xm - амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω - циклическая или круговая частота колебаний, t - время. Величина, стоящая под знаком косинуса φ = ωt + φ0 называется фазой гармонического процесса. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой.
 |
Частота колебаний f показывает, сколько колебаний совершается за 1 с. Единица частоты - герц (Гц), названная в честь немецкого физика Генриха Герца. Частота колебаний f связана с циклической частотой ω и периодом колебаний T соотношениями:
|
На рис. 2 изображены положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить экспериментально при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
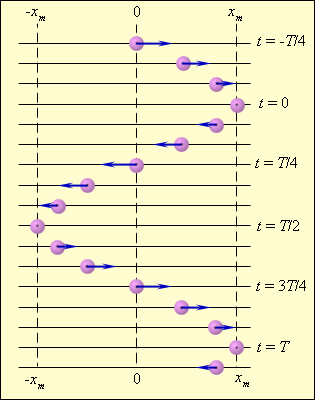 |
| Рисунок 2. Стробоскопическое изображение гармонических колебаний. Начальная фаза φ0 = 0. Интервал времени между последовательными положениями тела τ = T / 12. |
Рис. 3 иллюстрирует изменения, которые происходят на графике гармонического процесса, если изменяются либо амплитуда колебаний xm, либо период T (или частота f), либо начальная фаза φ0.
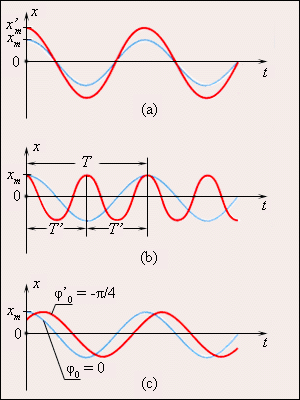 |
Рисунок 3. Во всех трех случаях для синих кривых φ0 = 0:
а – красная кривая отличается от синей только большей амплитудой
(x'm > xm); b – красная кривая отличается от синей
только значением периода (T' = T / 2); с –
красная кривая отличается от синей только значением начальной фазы
(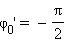 рад). рад). |
При колебательном движении тела вдоль прямой линии (ось OX) вектор скорости направлен всегда вдоль этой прямой. Скорость v = vx движения тела определяется выражением
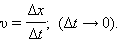 |
В математике процедура нахождения предела отношения 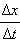 при Δt → 0 называется вычислением производной функции x(t) по времени
t и обозначается как
при Δt → 0 называется вычислением производной функции x(t) по времени
t и обозначается как  или как x'(t) или, наконец, как
или как x'(t) или, наконец, как  .
Для гармонического закона движения
.
Для гармонического закона движения 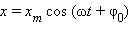 вычисление производной приводит к
следующему результату:
вычисление производной приводит к
следующему результату:
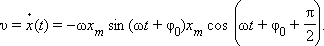 |
Появление слагаемого +π / 2 в аргументе косинуса означает изменение начальной фазы. Максимальные по модулю значения скорости v = ωxm достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = ax тела при гармонических колебаниях:
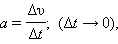 |
следовательно, ускорение a равно производной функции v(t) по времени t, или второй производной функции x(t). Вычисления дают:
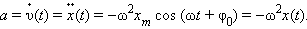 |
Знак минус в этом выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, по второму закону динамики сила, заставляющая тело совершать гармонические колебания, направлена всегда в сторону положения равновесия (x = 0). На рис. 4 приведены графики координаты, скорости и ускорения тела, совершающего гармонические колебания.
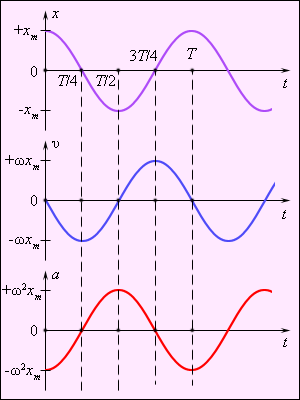 |
| Рисунок 4. Графики координаты x(t), скорости v(t) и ускорения a(t) тела, совершающего гармонические колебания. |
|
|