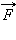– сила натяжения нити в нижней
точке траектории.Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
| A = –(Ep2 – Ep1). |
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
| A = Ek2 – Ek1. |
Следовательно
| Ek2 – Ek1 = –(Ep2 – Ep1) или |
|
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов динамики. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
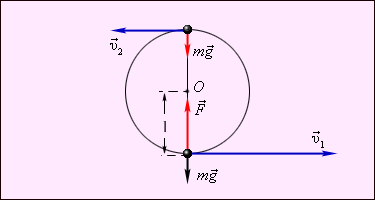
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Х. Гюйгенса). Рис. 1 поясняет решение этой задачи.
|
| Рисунок 1. К задаче Христиана Гюйгенса. 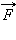– сила натяжения нити в нижней
точке траектории. |
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
 |
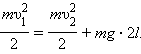Обратим внимание на то, что сила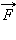 
натяжения нити всегда перпендикулярна скорости тела; поэтому она
не совершает работы. При минимальной скорости вращения натяжение нити в верхней
точке равно нулю и, следовательно, центростремительное ускорение телу в верхней
точке сообщается только силой тяжести:
 |
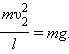Из этих соотношений следует:
 |
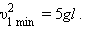Центростремительное ускорение в нижней точке создается силами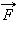 
и 
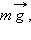направленными в противоположные
стороны:
 |
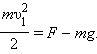Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
| F = 6mg. |
Прочность нити должна, очевидно, превышать это значение. Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач. В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды. Сила трения не является консервативной. Работа силы трения зависит от длины пути. Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии. Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии (рис. 2).
 |
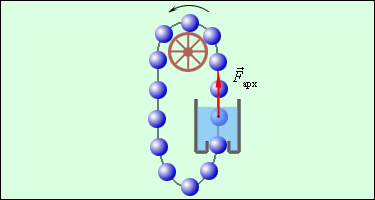| Рисунок 2. Один из проектов «вечного двигателя». Почему эта машина не будет работать? |
История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.
|
|
 |
