ДЖ. ЛАРМОР
ЭФИР И МАТЕРИЯ
Главы из книги “AETHER AND MATTER”,
Cambridge, 1900, p. 162— 193.—
Перев. с англ. Н. И. Надеждиной и Ю. И. Иваньшина.Глава X
ОБЩАЯ ПРОБЛЕМА ДВИЖУЩЕЙСЯ МАТЕРИИ, РАССМАТРИВАЕМАЯ ПРИМЕНИТЕЛЬНО К ОТДЕЛЬНЫМ МОЛЕКУЛАМ
Формулировка проблемы
Представим теперь, что материальная система состоит из свободного эфира, наполненного системой электронов, каждый из которых должен быть рассмотрен индивидуально. Некоторые из электронов являются свободными, но в большинстве своем они сгруппированы в материальные молекулы. Мы попытается сравнить относительные движения таких электронов в двух случаях: когда они образуют материальную систему (или принадлежат к материальной системе), не совершающую поступательного движения в эфире, и когда система как целое движется относительно эфира, скажем для краткости, со скоростью
v параллельно оси х. Средой, в которой развиваются события, в нашем конкретном случае является сам свободный эфир, уравнения динамики которого были точно установлены двумя совершенно независимыми путями — из рассмотрения оптической и электродинамической сторон его проявления, так что на этот счет в нашем анализе не будет ничего гипотетического. Электрон е будет представлен как особая точка в эфире, при подходе к которой упругое напряжение, составляющее эфирное смещение (/, g, к), неограниченно увеличивается пропорционально—eKn-{dldx, d/dy,. d/dz) /-1.
Это фактически аналогично тому, что называют простым полюсом в двумерном представлении, используемом в теории функции комплексного переменного. Предполагается, что эта сингулярность представляет собой определенную структуру, образующую в эфире ядро напряжения, которое способно перемещаться в среде независимо от движения самого эфира; вместе с электроном при его движении перемещается и связанная
с ним “порция” окружающего эфирного напряжения, описываемого вектором смещения (/, g, h), пропорциональная, как указывалось выше,— e/An-(d!dx, d/dy, d/dz)r~l.
Следует заметить, что энергия этой части смещения сконцентрирована вокруг ядра электрона, а не распространена на большую область, как могло бы показаться на первый взгляд. Эфирное смещение удовлетворяет условию потока
dfldx + dgldy + dhldz = 0, если в рассматриваемом элементе объема нет электронов. Последние аналогичны так называемым источникам и стокам в абстрактной теории жидкостного потока, так что при наличии электронов интеграл от нормальной составляющей эфирного смещения по границе какой-либо области вместо того, чтобы быть равным нулю, равен 2е — числу электронов, находящихся внутри этой области. Другой связанный с эфиром вектор, вектор магнитной индукции (а, Ь, с), также обладает свойством потока, но в его распределении нет особых точек, обладающих свойствами простых полюсов. Однако движение электрона включает сингулярность в (а, Ь, с) ротационного типа с ядром,, совпадающим с движущимся электроном.А именно: по мере того как расстояние г от него уменьшается неограниченно, магнитная индукция стремится к
evr-i sin 9, имея направление, перпендикулярное к плоскости угла 9 между г и скоростью v электрона. Это возникает как возмущение среды, стремящейся вывести электрон из его исходного положения и восстановить его в новом положении, в которое он перешел. Соотношения станут более явными, когда будут представлены в кинематических выражениях Приложения Е или когда мы перейдем к пределу в формулах гл. XI, относящейся к полю движущегося заряженного тела конечных размеров. Описание в тексте, как простого полюса, применимо к электрону, движущемуся со скоростью v, когда членами порядка (и/с)2 пренебрегают. В противном случае поле эфира, расположенного в непосредственной близости от него, не изотропно, и выражение для него необходимо заменить более точным, полученным в гл. IX. При обсуждении второго порядка в главе XI эта более точная форма привлекается неявным образом. При этом определяется напряжение электрона (п. 111) по концентрации смещения эфира вокруг него. Сингулярность магнитного поля, которая участвует в движении электрона (конечно, не внутренняя), не имеет концентрации.Среднее по времени этой сингулярности для квазистационарного орбитального движения электрона на расстояниях, значительно превышающих размеры орбит, аналитически эквивалентно магнитному дублету, что аналогично источнику и связанному с ним равному стоку. Наконец, предполагается, что различные части эфира пребывают в покое, так что” изменение во времени, например, напряжения какого-либо элемента эфира выражается производной по времени без каких-либо дополнительных членов, представляющих изменение напряжения за счет элемента эфира, перенесенного тем временем в новое положение.. В этом отношении уравнения для эфира, будучи фактически линейными, намного проще уравнений гидродинамики. Эфир неподвижен в этой теории, в то время как молекулы, из которых состоит Земля и все другие материальные тела, пролетают через эфир, не вызывая в нем никакого заметного движения. Благодаря этому строго выполняется закон астрономической аберрации света и остается в силе доплеровское изменение длины волны излучения движущегося источника. Но окажется, что все чисто
земные оптические явления не зависят от движения Земли.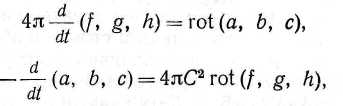
где символом rot (а, Ь, с) обозначают по Максвеллу вектор (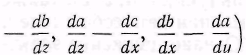
Для чисто аналитического развития схемы эфира, сформулированной выше, нет необходимости в конкретном физическом лредставлении строения эфира, поскольку существенную основу такого подхода уже образуют абстрактные соотношения и условия, приведенные выше. Фактически эти аналитические соотношения являются одними из идеально простых для такой цели, так как они дают в явном виде изменения во времени интересующих нас векторов, поэтому, зная состояние системы в какой-либо момент времени /, можно немедленно получить состояние в момент
t + dt и так последовательными шагами или с помощью разложения в ряд Тейлора можно определить состояние системы в любой будущий по сравнению с t момент времени. Вопрос, требующий особого внимания, заключается в следующем: определяет ли решение этих уравненийпри заданном начальном состоянии системы движение электронов (или ядер напряжения) через среду, а также изменения напряжения в самой среде. Из дальнейшего рассмотрения будет видно, что при подходящих гипотезах дело обстоит именно так, поскольку заданное начальное состояние будет заключать в себе и данные о движениях электронов, т. е. начальное условие для (а,
b, с) будет включать ротационные сингулярности около электронов по направлениям их движения, именно такие, которые за интервал времени Ы переместят электроны в новые положения, и так последовательно шаг за шагом.Однако при этом предполагается, что ядро электрона очень лабильно в своем движении через эфир. Иными словами, на это движение не влияет ни инерция, ни какие-либо другие силы, кроме тех,, которые выражают связь электрона с эфиром. Мы предполагаем фактически при этом полноту приведенной выше эфирной схемы связи.. Любую трудность, которая может появиться из-за бесконечных значений векторов в
самом ядре, можно устранить способом, обычным в аналитических работах по тяготению: будем предполагать, что ядро представляет собой объемное распределение электричества очень большой, но конечной плотности. В таком случае электричество не абсолютно сконцентрировано в точке, а распределено в очень, малом объеме, вследствие чего значения векторов остаются конечными. Относительно детальной структуры электронов не делается никаких предположений, поскольку размеры их ядер чрезвычайно” малы по сравнению с расстояниями между ними; допустимо рассматривать их как точки, подобно тому как, например, в общей теории тяготения планеты солнечной системы рассматривают как притягивающие точки. Этот метод является неполным только потому, что не рассматривает энергию и другие величины, связанные с взаимодействием частей самого электрона, поскольку они существенны только внутри молекул.Следует заметить, что согласно развиваемому здесь подходу, в котором атомы вещества рассматриваются как совокупности электронов, взаимодействие между атомами может быть описано только через электрические силы. Электрический характер сил химического сродства был составной частью воззрений Дэви, Берцелиуса и Фарадея. И более поздние дискуссии по этому вопросу, устраняя грубые концепции, непременно стремились к утверждению этой, гипотезы. До сих пор совершенно не разработан подход, в котором с этой точки зрения рассматривались бы обычные силы сцепления. Однако подобные трудности не ощущались как фундаментальные трудности атомно-вихревой картины строения вещества, пленившей высокие авторитеты молекулярной физики. Даже в конкретной реализации максвелловской теории эфира, на которую мы ссылались выше, атом вещества обладает всеми динамическими свойствами вихревого кольца в жидкости, лишенной трения, так что все, что может
быть сделано в рамках представлений о вихревых кольцах, неявно присоединяется к настоящей схеме. Тот факт, что успеха в области сил сцепления не достигли, в сущности, не является веским возражением против развития теории подобного рода, ибо целью теоретической физики не является полная и незамедлительная победа над “modus operandi” явлений природы. Это безнадежно недостижимо, хотя бы по той причине, что аппарат мышления, с помощью которого мы проводим исследования, сам является в одном из его аспектов частью схемы Природы, которую он пытается объяснить. Это очевидная истина. Истина, которая доказывает наличие корреляции между процессом мышления и процессами внешних явлений и которая заставляет продвигаться вперед, чтобы составить более четкую и ясную картину этих взаимосвязей. Без тени сомнения мы сводим взаимосвязи большой области физических явлений к их простейшим элементам, ибо не знаем, как применить старые принципы для объяснения новых явлений, к которым их, по-видимому, можно было бы применить, но которые находятся в основном за пределами досягаемости непосредственного эксперимента.Естественнее всего было бы предположить, что схема, с успехом работающая в области макроскопических физических явлений, которые мы можем подробно исследовать, должна иметь место (при соответствующих изменениях и добавлениях, касающихся различий в масштабах) и в микромире, недоступном для непосредственного детального изучения. И в любом случае (какого бы взгляда мы ни придерживались относительно необходимости
детального объяснения химического взаимодействия подходящей физической схемой) накладывается ограничение, как только мы начинаем рассматривать живую природу: любой законченный анализ условий жизнедеятельности, когда исключаются внешние результаты явлений, должен оставаться за пределами наших мыслительных способностей. Задача научного объяснения заключается фактически лишь в том, чтобы устанавливать правильные соотношения в запутанном лабиринте явлений природы, а вовсе не в том, чтобы давать исчерпывающую схему этого лабиринта. Теория, адекватно отображающая взаимосвязи какой-либо области явлений природы, сохраняет свое право на существование до тех пор, пока она не окажется в противоречии, неустранимом подходящей модификацией, с какой-либо другой областью явлений природы.Движущиеся материальные среды (приближение первого порядка)
Вернемся теперь к уравнениям свобод-ного эфира и перейдем от покоящихся относительно эфира осей (х, у, г) к осям (х'
, у', г'), движущимся с поступательной скоростью параллельно оси х. Благодаря этому мы сможем исследовать, как меняются явления, когда наблюдатель движется с постоянной скоростью относительно покоящегося эфира. Эти уравнения имеют вид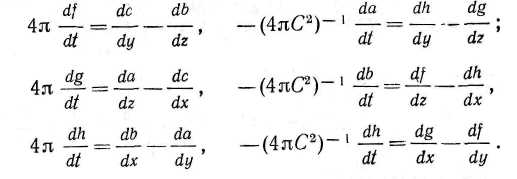
Поскольку при переходе к движущейся с постоянной скоростью системе координат (х
1, у', г') = (х — vt, у, z), t' = /, следовательно, dldx, dldy, dldz будут d/dx', dldy', dldz', a dldt заменится на dldt' — — v-dldx', уравнения примут вид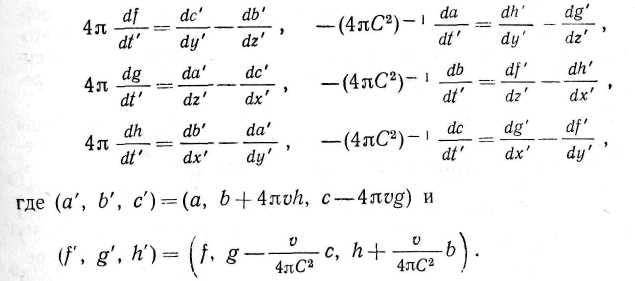
Используя две последние формулы, можно полностью исключить (/> g> Щ и ("• ь< с) так
, чтобы остались только штрихованные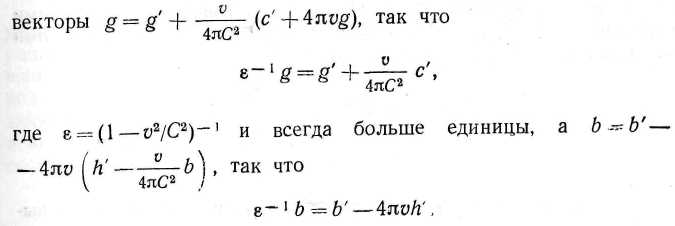
В результате получаем общие соотношения:

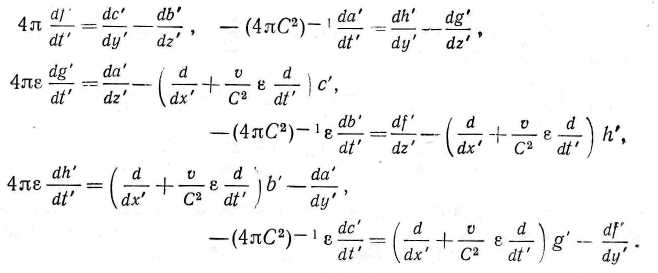

Заменим теперь
t на t" — t' — (vlC2)dx.(Именно такое преобразование временной координаты было применено Лоренцем в работах 1892 и 1895 гг. (Arch. Need., 1892, b. 25, s. 363; Versucb einer Theorie der elektrischen und optischen Erscheimmgen in bewegten Korpern (Leiden, 1895)). В общем виде местное время с начальным отсчетом, зависящим от пространственной координаты, было введено еще раньше Фогтом в работе “О принципе Доплера” (Gott. Nachr., 1887, p. 41). — Прим. ред.)
Это приведет к тому, что
(d/dx') + (u/C2)e (d/dt') заменится на dldx', в то время как другие дифференциальные операторы останутся неизменными. Благодаря этому уравнения принимают вид, который они имели в покоящейся системе отсчета, если не обращать внимания на множители е в их левых частях.107. Следует заметить, что множитель е отличается от единицы только на
v/C2, т. е. на бесконечно малую второго порядка, пренебрегая которой, мы получим следующую картину. Рассмотрим какую-либо электродинамическую систему, и пусть спонтанные изменения, происходящие в ней, описываются в движущейся относительно эфира с постоянной скоростью (о, 0, 0) системе координат (х', у', г') векторами (/, g, h) и (а, Ь, с), представленными как функции переменных х', у', г' и t'. Последняя величина представляет собой время, измеряемое обычным путем. Тогда существует соответствующая (correlated) покоящаяся относительно осей (х', у', г') электродинамическая система, такая, что описывающие ее спонтанные изменения векторов (/', g', h') и (а', Ь', с') являются функциями переменных х', у', г' и t" = t' — (vlC2)x', функциями точно такими же, как и те, которые представляют величины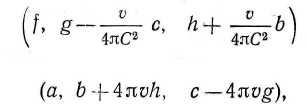
относящиеся к соответствующей движущейся системе, когда они выражаются через переменные х', у', г' и
t'. Теперь, наоборот, возьмем какую-либо покоящуюся в эфире электродинамическую систему. Пусть она описывается векторами (/', g', h') и (а', Ь', с'), выраженными как функции координат (х, у, z) и времени г'. Заменим в этих функциях f на t — (v/C2)x. Тогда результирующие выражения являются значениями величин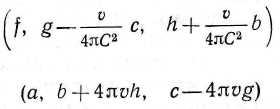
для электродинамической системы, движущейся относительно эфира с постоянной скоростью, если рассматривать это движение в координатах (х, у, г), движущихся вместе с ней, а в качестве временной переменной взять /. Сравнивая состояния этих двух систем, мы имеем с точностью до величин первого порядка:
Поэтому электроны в обеих сравниваемых системах, будучи расположенными в особых точках, где перестает убывать концентрация электрического смещения, занимают соответствующие положения. Далее, мощности
[Этим термином автор обозначает количество электричества в объеме электрона. — Прим. перев. (strengths) ] этих электронов равны, так как вблизи электрона (независимо от того, движется ли он или покоится) значения (/, g, h) и (а, Ь, с) практически определяются им самим, а вклад остальной части системы пренебрежимо мал. В этой связи соотношение между (/, g, h) и (/',#', ti) есть, согласно п. 106: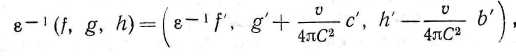
и тогда, поскольку для одиночного покоящегося электрона (а', Ј>', с') равно нулю, вблизи связанного электрона в движущейся системе (/,
g, h) равно if', &g', e/i'), где е = [1 — (irVC2)]-1 отличается от единицы на бесконечно малую второго порядка. Таким образом, пренебрегая бесконечно малыми второго порядка, мы имеем (/, g, h) = = (/'> g'> h') для соответствующих точек, расположенных очень близко к электронам, и, поскольку количество электричества внутри любой замкнутой поверхности равно интегралу от нормальной составляющей эфирного смещения по этой поверхности, взяв достаточно малую поверхность вокруг электрона, мы получим в этом приближении одинаковые мощности электронов в двух системах.Следует отметить, что рассмотренное выше аналитическое
преобразование уравнений применимо к любой изотропной диэлектУстановленное соотношение между электродинамической
системой, отнесенной к неподвижным осям-, и системой, отнесеннойКроме того, этот результат не зависит от природы сил, действующих между молекулами вещества: предполагается, что структура вещества и все электрические распределения не меняются (в приближении первого порядка) при движении в эфире. Все доказанное сводится к тому, что если какая-либо конфигурация ионных зарядов является естественной в покоящейся материальной системе, то сохранение этой конфигурации относительно равномерно движущейся системы не потребует каких-либо новых вспомогательных сил. Электрон, взятый сам по себе, должен быть в любой мыслимой
теории простой сингулярностью эфира: его перемещения, когда он свободен, и взаимодействия с другими электронами, если он окружен материей, прослеживаются с помощью дифференциальных уравнений одного лишь окружающего свободного эфира. А корреляция между этими уравнениями установлена для двух случаев, которые сравнивались выше. Следует заметить, однако, что, хотя неподвижная и движущаяся системы электронов при такой корреляции являются в соответствующих случаях идентичными, их электрические и магнитные смещения отличаются членами первого порядка.Глава XI
ДВИЖУЩАЯСЯ МАТЕРИАЛЬНАЯ СИСТЕМА
(ПРИБЛИЖЕНИЕ ВТОРОГО ПОРЯДКА)
Приближение первого порядка по
v/C, полученное выше, было выведено из соответствиями, п. 106) между уравнениями для векторов, обозначенных (/', g', h') и (а', Ь', с'), отнесенных к покоящимся относительно эфира осям (х', у', z') и времени t", и уравнениями для соответствующих векторов, обозначенных (/, g, h) и (а, Ь, с), отнесенных к движущимся поступательно с постоянной скоростью осям (х', у', z') и времени t'. Но мы можем пойти дальше и с помощью более полного преобразования установить соответствие, которое будет верным и во втором порядке. Обозначим, как прежде, t' — (v/C2)ex' через /". Тогда точные уравнения для (/, g, h) и (а, Ь, с), отнесенных к движущимся осям (х', у', z') и времени f, как показано выше, эквивалентны уравнениям: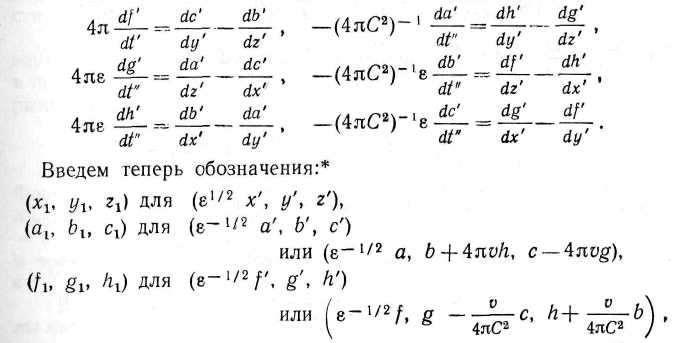
* Здесь автор впервые в движущейся системе вводит координаты (хи
ylt гъ ti), связанные с координатами (х, у, z, t) исходной системы релятивистскими преобразованиями, которые впоследствии стали называться преобразованиями Лоренца.— Прим. ред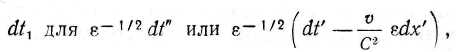
где е = [1 — {и
21 С2)]'1. Будет видно, что множитель е сокращается, так что система уравнений, отнесенная к движущимся осям, которая объединяет новые переменные с нижними индексами, по форме идентична максвелловской системе уравнений эфира, отнесенной к неподвижным осям. Такое функциональное преобразование (х!, у', z') в (*!, у1у гг) имеет смысл (применительно к данной проблеме) удлинения пространства в отношении в|/2 вдоль направления движения системы координат. Поэтому, если величины (/ъ gly hr) и (alt Ьи сх)у заданные как функции переменных xlt уъ zlt tlt выражают ход спонтанного изменения векторов электродинамической системы движущихся электронов, отнесенный к покоящимся относительно эфира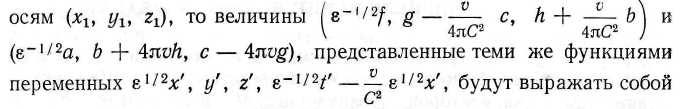
ход изменения векторов (/,
g, h) и (а, Ь, с) соответствующей электродинамической системы движущихся электронов, отнесенный к осям, движущимся поступательно относительно эфира с постоянной скоростью (v, 0, 0). При таком соответствии между двумя электродинамическими системами мы имеем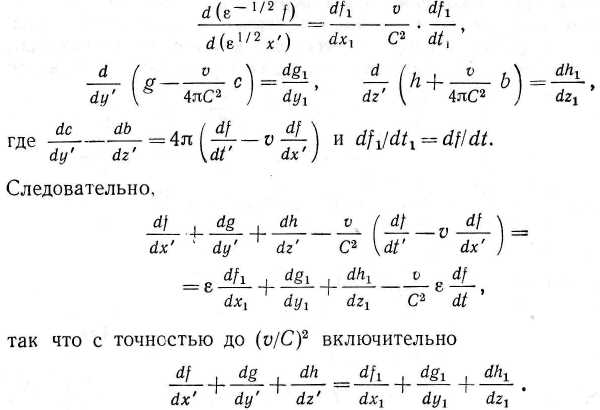
Таким образом, выводы относительно положений электронов в двух системах, которые были предварительно установлены в приближении первого порядка по и/С, остаются справедливыми и в приближении второго порядка, если считать, что размеры движущейся электродинамической
системы сокращаются вдоль направления еедвижения по сравнению с неподвижной системой в отношении е-"г или 1 — (1/2)(и
2/С2).111. Отношение мощностей соответствующих электронов в двух системах можно теперь вывести точно так же, как это было сделано раньше, когда мы ограничились обсуждением лишь первого приближения по
v/C. В случае единичного равномерно движущегося электрона сравнение проводится с единичным покоящимся электроном, вблизи которого величина (аь blt cx) стремится к нулю, поскольку она зависит от этого электрона. В общем случае мы имеем теперь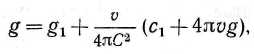
следовательно, для единичного электрона
(g, h) = e (glt кг), тогда как / = el/2fv Но мощность электрона в движущейся электромагнитной системе представляет собой значение интеграла || (fdy'dz' + + gdz'dx' + hdx'dy'), взятого по любой как угодно малой поверхности вокруг ядра электрона, так что мощность каждого движущегося электрона &112 Ц (fidy^Zx + g1dz1dx1 -f- hxdxxdy^) равна мощности соответствующего покоящегося электрона, умноженной на е1/2. Этот аргумент применим, как и прежде, даже и в присутствии других электронов, если электрон окружить достаточно малой поверхностью интегрирования, поскольку тогда значение каждого вектора будет в основном определяться только этим электроном (Этот результат сразу же следует из п. 110, в котором показано, что соответствующие плотности зарядов равны, в то время как объемы относятся как е I к единице.).112. Однако перед нами стоит задача установить такое соответствие между движущейся и покоящейся относительно эфира электродинамическими системами, при котором мощности электронов были бы равны, а не пропорциональны, поскольку движение материальной системы, содержащей электроны, не может изменить их мощности. Это вытекает из принципа динамического подобия.
Фактически, мы должны уменьшить масштаб электрических зарядов, а следовательно, и величины
dfldx + dgldy + dhldz в покоящейся системе в отношении е'^2. Применим поэтому преоб-оазование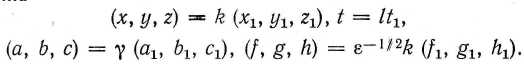
Форма основных вихревых уравнений эфира не изменится, если положить
k = / и у = &~l>2k. Пусть теперь k и / равны единице, а 7 = = е~'^2, так что мы требуем не изменения масштаба пространства и времени, а только уменьшения величины (а, Ь, с) в отношениие
-!/2_Во втором приближении мы получаем, что если внутренние силы материальной системы, все без исключения, являются следствием электродинамического взаимодействия между электронами, обра-
Следующими атомы, то эффект приведения стабильной материальной системы в движение с постоянной скоростью заключается в том, чтобы создать равномерное сжатие системы в направлении движения, пропорциональное величине е~'/
2 = [1 — (1/2)(и2/С2)]. Электроны займут соответствующие положения в этой сжатой системе, а эфирные смещения в пространстве вокруг них не будут такими же, как и в неподвижной системе: если (/, g, h) и (а, Ь, с) — эфирные смещения в движущейся электродинамической системе, то электрическое и магнитное смещения в соответствующих точках покоящейся системы будут представлять собой значения, которые векторы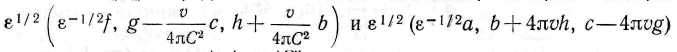
имели во время const +
vx/C2 до рассматриваемого момента, когда масштаб времени возрос в отношении е1^2.Из того что электрический и магнитный векторы излучения лежат в плоскости фронта волны, следует соответствие относительных волновых фронтов излучения в двух коррелированных электродинамических системах — неподвижной и движущейся, такое же, как и соответствие лучей, являющихся путями распространения лучистой энергии систем. Изменение временной переменной при сравнении излучений в неподвижной и движущейся системах является причиной эффекта Доплера.
Цуги излучения и корреляция между
стационарной и движущейся средой.Рассмотрим даваемое выражением
(/i. Su ^i) = (L, M N) F (lxx + tny1 -f- nzx — pt)
эфирное смещение, связанное с плоским волновым цугом, распространяющимся вдоль направления (/, т, п) со скоростью
V (или С1\а, где р. — коэффициент преломления, равный р (I2 + /л2 + л2)"'/2) в покоящейся материальной среде, отнесенной к системе координат (хх, ух, zx). Векторы (/, g, h) л (a, b с) в соответствующем волновом цуге в такой же, но движущейся и потому сжатой в указанном выше смысле среде, определяемой координатами (х, у, z), удовлетворяют соотношению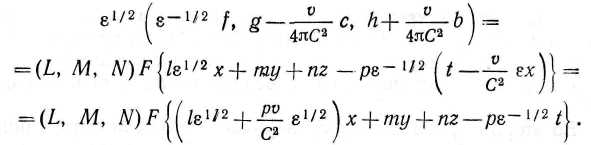
Так как волновой цуг в покоящейся среде поперечно поляризован, так что векторы (/,
g, h) и (а, Ь, с) оба лежат в плоскости фронта волны, то это же самое справедливо и для векторов (/, g, h), (a, Ь, с) соответствующего волнового цуга в движущейся системе. Фактически этого следовало ожидать исходя из вихревого свойства этих векто-ров: вектор направления фронта цуга в движущейся среде пропорционален (/е
|/2 -f-— &1>2,т, /г),а его скорость распространения есть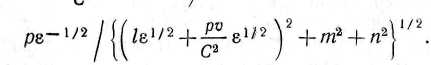
Таким образом, когда волновой цуг распространяется со скоростью
V вдоль направления движения материальной среды, т. е. вдоль оси х, так что тип равны нулю, скорость цуга относительно этой среды будет V&~4[1 + (Vv/C2)], или, с точностью до величин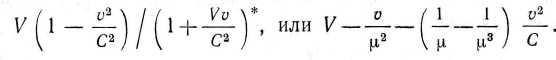
Второй член в этом выражении представляет собой эффект Френеля, а последний член — поправка второго порядка согласно нашей гипотезе, которая объясняет отрицательный результат опыта Майкельсона.
В общем случае длина волны цуга излучения в движущейся материальной системе отличается от длины волны соответствующего
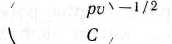
цуга в покоящейся системе множителем I I -f 2/
—^ ) или 1 —— lv/\iC,
где / — косинус угла наклона луча к направлению и, т. е. длина волны в движущейся электродинамической системе короче на величину, пропорциональную v/C, которая представляет собой эффект Доплера, поскольку период (с точностью до v/C) не меняется.Если волновой фронт в движущейся среде распространяется в плоскости ху под углом 0 к направлению движения среды, так что п равно нулю, то скорость V" волнового цуга (длина волны которого изменилась) относительно среды дается выражениями:
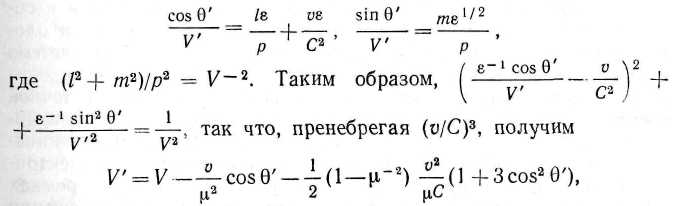
* Это соотношение, полученное Лармором для скорости светового фронта в движущейся среде, давало объяснение опыту Физо и выражало новый закон сложения скоростей, согласно которому скорость светового фронта относительно исходной системы равна
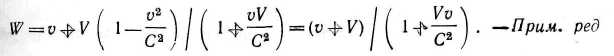
где ц = CIV. Последний член представляет собой общую форму поправки второго порядка к формуле Френеля. В свободном эфире, где \л = 1, это выражение дает скорость неизменного волнового цуга относительно движущихся осей, как это и должно быть.
Поскольку
(f,g, h) и (а, Ь,с) находятся в одинаковой фазе в свободном проникающем эфире, то когда один из них равен нулю, равенВлияние поступательного движения на структуру молекулы
Закон сохранения массы
В качестве простой иллюстрации общей
молекулярной теории рассмотрим пару электронов противоположных знаков, описывающих стационарные круговые орбиты один вокруг другого, когда такая система не совершает поступательного движения в эфире [В этом примере предполагается, что орбитальные скорости так малы, что излучение не имеет места.]. Мы можем убедиться, что, когда такая пара движется в эфире в плоскости орбит электронов, эти орбиты будут сплющиваться по направлению v пропорционально 1 — (1/2)(и2/С2) и превратятся в эллипсы. В это же время будет иметь место пропорциональное v/C замедление орбитального движения электрона, когда он приближается к среднему положению, и ускорение, когда электрон проходит его, так что в целом период изменится только на величину второго порядка отношения vIC. Подобным образом можно учесть влияние поступательного движения и в общем случае, когда направление этого движения наклонно к плоскости орбиты или когда как угодно сложная орбитальная система электронов составляет идеальную молекулу. Но это утверждение подразумевает, что ядро электрона является просто особой точкой в эфире, что в нем не заключено ничего такого, чья природа инерции была бы чужда эфиру. Это подразумевает также, что нет никаких других сил между электронами, кроме определенных электрических сил, которые существуют только благодаря эфиру. В рамках нашего подхода обстоятельство, что изменения периодов обращения электронов при движении молекул в эфире являются величинами второго порядка по о/С, существенно для теории спектроскопических измерений лишь при космических скоростях. Этот вывод, однако, остался бы в силе, если бы мы предположили, что молекула имеет не связанные с эфиром инерцию и потенциальную энергию, которые не зависят от равномерного движения. В этом случае существующие в молекуле эфирные поля (свободные или ограниченные) движущихся электрических зарядов будут продольно симметричными и постоянными в первом приближении. Поэтому на них не влияет изменение знака скорости поступательного движения, так что частоты свободных колебаний не могут включать в себя первую степень этой скорости.Тот факт, что равномерное движение молекулы через эфир
не нарушает ни ее строение (в первом приближении), ни продольную-Множитель перед половиной квадрата поступательной скорости молекулы является (в том же приближении) мерой инерции, или массой, молекулы с таким строением. Отсюда, пренебрегая
1 величинами второго порядка, получим, что электрическая инерция молекулы равна сумме инерции составляющих ее электронов,. а фундаментальный химический закон постоянства массы при молекулярных преобразованиях проверяется для той части массы, которая имеет электрическую природу.Против точки зрения, что вся инерция молекулы связана
с электрическим действием, возникло возражение на основании того,.* По-видимому, автор имел в виду энергетические соображения. —Прим. ред.
|
|