На основе математически правильных расчётов Ньютоном был построен физически неправильный ход лучей в призме, противоречия которого с действительностью легко обнаружить экспериментально. С тех пор, по мнению автора, «математическая физика» не гнушается предписывать природе правила поведения. Показано, что в призме имеют место два процесса — преломление световых лучей на входе в призму и преобразование их на выходе из неё. Солнечные лучи и лучи солнечного спектра обладают различными свойствами.
1. В чём разница между стеклом призмы и стеклом толстой пластины?
Пересечение световым лучом толстой пластинки в учебниках показывают так, как на рис. 1.
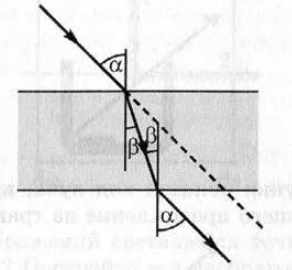
Рис. 1
Входной и выходной лучи параллельны друг другу, цвет лучей не меняется.
Разложение же лучей в призме показывают так, как на рис. 2. Сразу при входе в стекло призмы луч света расщепляется на множество цветных лучей.

Рис. 2
Почему свет на входе в стекло должен вести себя так по разному? Почему лучи света при входе в призму расщепляются, а при входе в точно такое же стекло толстой пластины это расщепление не имеет места?
Если правилен рис. 2, а он напечатан в миллионах учебников, не только в России, но и на Западе, то и при входе в толстую пластинку (толстое стекло) лучи также должны были бы расщепляться на цветные лучи, так, как показано на рис. 3. Но такого никогда не бывает. При проходе через плоско-параллельный слой (толстое стекло) свет
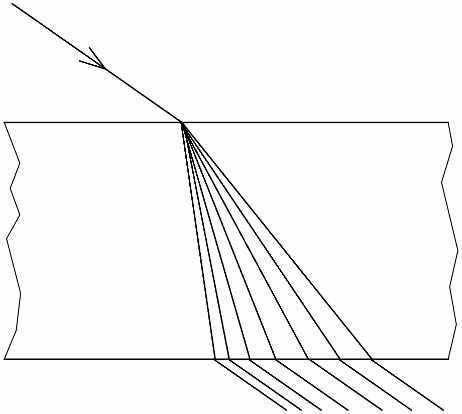
Рис. 3
никогда не разлагается и ширина луча тоже не меняется. Мы имеем какое-то странное противоречие. Свет ведёт себя нелогично?
К счастью, в данном случае виноват вовсе не свет, а человеческая логика. Причина недосмотра, о которой будет более подробно сказано позже, лежит в слепом доверии математике и отсутствии достаточной наблюдательности.
Физика — это логичность и наблюдательность при проведении экспериментов и их толковании. Но на наше внимание при проведении и толковании экспериментов воздействует множество факторов. Возможно, наихудший из них — увлечённость какой-либо недостаточно обоснованной идеей, под которую мы невольно подгоняем наше толкование экспериментов. В соответствии с этим один из исследователей посчитал, что световые лучи должны идти именно так, как показано на рис. 2. Ему это показалось логичным и обоснованным. Его последователи не смогли увидеть явное нарушение логики и поверили его точке зрения. Но вечная природа не обращает внимания на подобное. Она рассудила немного иначе .
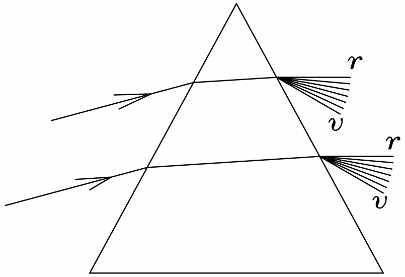
Рис. 4. Разложение лучей света происходит только на выходе из призмы. Буквами r и v помечены крайние световые лучи в разложении, красные и фиолетовые.
На самом деле лучи входят в призму точно так же, как и в толстую пластину и не разлагаются при этом (рис. 4). Разложение происходит только при выходе каждого луча из призмы [1]. Казалось бы, теперь всё нормально. Рис. 1 и рис. 4 соответствуют друг другу. Луч внутри стекла не разлагается. Никакого нарушения логики нет. Но увы, это не совсем так. Мы получили однообразие поведения света только внутри стекла призмы и толстой пластины. При выходе из стекла треугольной призмы на рис. 4 лучи разлагаются, а на рис. 1 при выходе из плоско-параллельного слоя нет. Почему? Опять противоречие. Свет всё-таки ведёт себя нелогично?
Нам хотелось бы, чтобы свет вёл себя всегда логично, чтобы мы всегда могли применять одни и те же правила поведения света, чтобы мы могли предсказывать ход лучей. К сожалению, пока ещё никто не может во всех случаях предсказывать поведение света [2]. Но для рис. 1 и 4 можно сделать предположение, которое всё приведёт в порядок. Надо предположить, что свет при входе в оптически более плотную среду меняет своё состояние . Встречая при выходе из неё плоскость, параллельную входной, он восстанавливает своё прежнее состояние, его луч снова будет параллелен входному и цвет белого луча будет попрежнему белым.
Во всех иных случаях прежнее состояние не восстанавливается и белый луч может разложиться на множество цветных лучей.
Итак, всё дело в наклоне друг к другу граничных поверхностей проходимого светом оптически более плотного слоя.
Теперь у нас для обоих случаев общее описание поведения света. Это произошло за счёт введения понятия особого состояния светового луча внутри оптически более плотной среды.
2. О применимости закона преломления света
Мы решили проблему качественно. Но будет ли поведение световых лучей соответствовать и количественным зависимостям?
Уже несколько тысяч лет оптикам известно понятие
преломления света. При входе в оптически более плотную среду направление светового луча обычно изменяется (рис. 5).
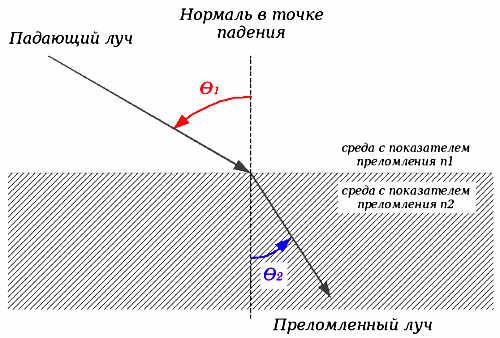
Рис. 5.
Правило, по которому это происходит, называется законом преломления света, законом Снеллиуса, законом синусов:
n1· sin Θ 1 = n2· sin Θ 2
В этой формуле n1 и n2 коэффициенты преломления сред, Θ 1 и Θ 2 углы падения и преломления соответственно.
На входе в призму мы можем спокойно применить закон преломления. На выходе же у нас возникает непреодолимая проблема. Угол падения у нас один, а углов преломления минимум семь — для каждого цвета лучей, которые принято изображать. Если мы обозначим углы преломления на выходе из призмы Θ2, Θ3, …, Θ8, то у нас получится семь уравнений:
n1 · sin Θ1 = n2 · sin Θ2
n1 · sin Θ1 = n2 · sin Θ3
n1 · sin Θ1 = n2 · sin Θ4
……
n1 · sin Θ1 = n2 · sin Θ8.
Все углы преломления у нас разные, но n2 (для воздуха) меняться не может, поэтому мы сможем удовлетворить в лучшем случае только одно из этих уравнений. (На самом деле, как мы знаем, цветных лучей бесконечное множество, а удовлетворить условие мы сможем только для одного луча).
Заметим теперь, что рис. 4 у нас не теоретический, а чисто экспериментальный. Мы можем несколько менять положение входного луча, но на выходе у нас всё равно всегда будет минимум семь лучей с разными углами преломления. В неправильности мы могли бы подозревать только закон преломления.
Но ведь закон преломления — он тоже экспериментальный? Положение, мягко говоря, безвыходное.
Может ли такое быть? Повторяю, у нас не данные теории, в которой можно было бы сомневаться, а данные эксперимента. Эксперимент, как сказал некто, это разговор с богом. Спорить мы не можем, но можем попытаться найти толкование.
Наша логика построена на словах. По Ньютону, белый свет состоит из определённой смеси цветов спектра. Если мы будем верить Ньютону, то выхода у нас нет. Пистолет к виску, во избежание позора, и…
Но не будем торопиться. Нас никто не видит, мы можем подумать. Ньютон хотя и полагал, что доказал своё утверждение экспериментально, но ведь всё дело в логической цепочке. Где-то должна быть ошибка. Заключается она, возможно, в том, что Ньютон считал полученное разложение стандартным. Но в статье [3]
приводился спектр, полученный с помощью призмы из плекса. Этот спектр оказался совсем иным. Как указывалось в статье [3], на основе этого факта мы можем считать, что разложение Ньютона стандартным не является. Исходя из этого, можно считать, что на рис. 4 на выходе из призмы представлено не разложение , а преобразование световых лучей. Наше спасение должно быть именно в этом слове. В случае преобразования нет преломленных лучей, а есть преобразованные. Они не обязаны подчиняться закону преломления.
Сделанный вывод не противоречит тому, что белый свет можно получить из смеси всех цветов радуги, или из нескольких других цветов. Почти любой цвет, который по заверениям Ньютона сам по себе является неразлагаемым и неизменяемым, можно в то же время получить из смеси нескольких цветов.
Но в любом случае мы получили, что закон Снелля должен иметь ограниченное применение. Для случая призматического разложения света на выходе из призмы он явно не применим.
3. Как должны вести себя лучи на поверхности преобразования?
Если лучи на выходной поверхности призмы не разлагаются, а преобразовываются, то они должны приходить и в некотором смысле останавливаться, исчезать. Преобразованные же лучи должны начинаться, возникать именно на поверхности преобразования. Посмотрим на рис. 4. Похоже, что всё соответствует именно этой картине. Приходящий луч как бы приходит, но не уходит. Вместо него появляется бесконечное множество цветных лучей. Но обнаруженный нами недостаток — невозможность применения закона о преломлении лучей — кажется непреодолимым. Что бы ни означал показатель преломления, он не может иметь бесконечное число значений в определённой точке. Но так как мы пришли к выводу, что на выходе из призмы мы имеем преобразование лучей, то о показателе преломления речи при этом быть просто не может. На входе коэффициент преломления существует, а на выходе он вовсе и не обязан быть. Ведь у нас имеет место преобразование .
В случае толстой пластины свет не преобразовывается и преломление имеет место как на входе луча, так и на выходе. В этом случае коэффициент преломления, который характеризует некоторое свойство вещества, должен быть одинаковым и на входе и на выходе. Всё хорошо. А в случае преобразования происходит нечто совсем иное и направление исходящих лучей может быт самым различным, и закон преломления здесь просто неприменим.
4. Миф — это не только полёт фантазии, но порой и точный математический расчёт. Математика может создавать мифы?!
Всё это хорошо, скажете вы, но ведь сейчас разложение света призмой отлично просчитывают, и оно вполне подчиняется закону преломления?
Всё дело в том, что при определении коэффициента преломления никто не учитывал, что случай призмы и случай толстой пластины в смысле преломления резко отличаются друг от друга. В случае толстой пластины имеет место только преломление, и потому коэффициенты на входе и на выходе обязаны быть одинаковыми. А в случае призмы мы на входе имеем преломление, а на выходе — преобразование лучей света. Это совершенно разные вещи. Если этого не учитывать, то здесь начинается страна чудес.
Представьте себе, что мы с помощью равнобедренной призмы составили таблицу коэффициентов преломления для лучей различной цветности. Делается это отдельно для луча каждого цвета при абсолютно симметричной картине хода лучей через призму. Подробнее это можно увидеть, например, в руководстве [4] по проведению подобных измерений в лаборатории.
Воспользовавшись этими данными и, исходя из того, что солнечный свет по Ньютону представляет из себя (механическое?) собрание лучей различной цветности, мы теперь можем построить ход солнечного луча через призму. При этом мы получим всем известную по учебникам картину, представленную на рис. 2. Нам говорят вполне убеждённо: «Это схема прохождения солнечного луча через призму».
Если среди нас окажется Фома Неверующий, то ему покажут и эксперимент с помощью проектора. Так как световые лучи невидимы, мы увидим только вход лучей в призму и радугу на экране. Но большего требовать нельзя, мы вынуждены согласиться с тем, что видели разложение света призмой во всех подробностях.
Кто был достаточно внимательным, тот понял, что нас «слегка» обманули.
Первое. Нам представили на схеме (рис. 2) не действительный ход лучей, а расчётный. Во-вторых, при построении хода лучей исходили из того, что солнечный свет состоит из набора семи независимых друг от друга лучей, чему мы должны были поверить без доказательства. В-третьих, на входе в призму мысленно применили не закон Снелля, а его модификацию, исходящую из того, что луч каждой цветности имеет в материале стекла свою собственную скорость, чего также не доказали. (Конечно, можно сказать, что нам не предоставляли никакой модификации закона Снелля, а экспериментальные данные о коэффициенте преломления для лучей различной цветности. Но как раз в этом и есть подмена. Наличие внутри призмы лучей различной цветности никем не доказана). В-четвёртых, нам не объяснили, почему свет, входя в призму, должен вести себя иначе, чем при входе в толстую пластину (рис. 1). В-пятых, нам сказали, что луч, входящий в призму, должен быть очень узким, но не сказали, насколько. Луч же проектора был довольно широкий.
А теперь внимание.
Если верить книге [5] акад. Вавилова о Ньютоне, примерно таким образом, как мы только что описали, проходили лекции Ньютона по оптике, за тем исключением, что у него не было проектора и потому он не мог показать студентам даже ложного экспериментального подтверждения своих расчётов. Тем не менее, мы должны верить заверениям Вавилова о том, что эксперименты Ньютона были очень тщательными и точными.
В статье [6] я представил дело так, будто мифы о ходе лучей в треугольной призме распространялись по незнанию. Это, разумеется, верно. Но теперь надо уточнить, что они распространялись не только по незнанию, но и в соответствии с точными математическими расчётами, и, возможно, первым их распространителем был сам Ньютон. Он не знал , как лучи света проходят по призме. Рассчитанную и нарисованную схему хода лучей в призме он не догадался сверить с тем, что он мог проверить на призме, и слепо верил своим расчётам. Они же были построены на предположении, которое он только пытался доказать, а сам считал доказанным.
Благодаря книге акад. Вавилова, мы, наконец-то, получили некоторое представление о том, что такое «математическая физика» и откуда пошёл миф о том, что математика — это царица наук и что каждый физик должен быть хорошим математиком.
Увы, нет. Любой физик должен быть прежде всего хорошим физиком. Но было бы очень неплохо, если бы математик, который пытается представить себя физиком высшей пробы , не путал математические расчёты с физическим экспериментом и ни в коем случае не подменял эксперимент расчётами. В этом случае нам бы не представляли многие статьи горе-физиков начала прошлого столетия как научную революцию и решение имевшегося якобы тогда кризиса физики. Всё как раз наоборот. Кризис физики резко обострился благодаря этим «революционным» математическим опусам, не имевшим ничего общего с физикой, в связи с тем, что их стали громко и навязчиво прославлять, не давая одновременно слова их оппонентам. В результате мы имеем то, что имеем (что нам навязывают).
Я уже неоднократно говорил о противоречиях, которые легко обнаружить при простейших проверках схемы разложения света по рис. 2. Но мне кажется уместным упомянуть здесь некоторые противоречия ещё раз. Любой может заметить, что если на рис. 2 рядом со входным лучом параллельно ему поместить поблизости ещё несколько лучей, то картины разложения лучей наложатся друг на друга и разложение будет испорчено. Это отлично «знает» и скажет вам любой преподаватель физики. Но его может легко опровергнуть «радуга», получаемая при помощи аквариума. Ширину пучка солнечного света, падающего на аквариум, никто никогда не ограничивает, но радуга может получиться отличной и очень яркой. Её можно хорошо видеть на полу или на стене. Никакого затемнения комнаты при этом не требуется.
Как Ньютон, отличающийся такой высокой «точностью в экспериментах», мог не проверить того факта, что пучок света, падающий на призму, может иметь любую ширину. Уже по этой мелочи он мог бы понять, что его расчёты неправильны.
Я обычно привожу рисунок разложения света по Ньютону с призмой, на которой расположена пластинка 1 (рис. 6), передвигая которую по поверхности призмы, можно было бы гасить цвета радуги один за другим. Но увы, на деле это не получается. А это говорит о том, что действительный ход лучей по рис. 6 (или по рис. 2) представлен неправильно.
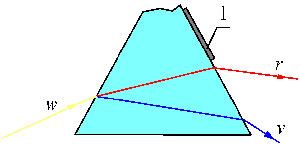
Рис. 6. Разложение света по Ньютону.
Здесь w означает белый, r – красный, а v – фиолетовый лучи (для простоты рисунка промежуточные цвета радужного спектра не показаны).
Я повторяю это здесь ещё раз в связи с тем, что подобным образом можно было бы разделить солнечный спектр на две части. Эту задачу Ньютон решал гораздо более сложным путём, о чём сказано в главе 5 (схема решения Ньютона показана на рис. 15) уже упомянутой книги [5] акад. Вавилова. Вавилов восхищается остроумностью схемы этого опыта Ньютона. Но остроумными обычно называют более простые методы решения. Это говорит о том, что как Вавилов, так и Ньютон слишком плохо представляли себе схему разложения света по рис. 2 или 6 и оба не знали об этой „возможности“ разделения солнечного спектра на две части. Испытав же эту «возможность» в соответствии с рис. 6, Ньютон понял бы, что его расчёты почему-то неправильны. Ход лучей должен быть иным. Если бы он это сделал, оптика могла бы пойти несколько иным путём [7].
Вавилову эта оплошность простительна, но как мог не заметить эту «возможность» Ньютон, занимавшийся оптическими экспериментами 16 лет? И, кроме того, много лет читавший лекции по оптике?
Но, похоже, человеку, видящему мир глазами математика, и всячески восхваляемому известными средствами (дез)информации, подобная слепота в вопросах физики нисколько не мешает на пути к мировой славе «выдающегося физика и математика».
5. Слава Ньютону! Слава его ошибкам!
Своими расчётами Ньютон, похоже, доказал противоположное тому, что хотел доказать. Если бы солнечный луч действительно был смесью независимых друг от друга лучей различной цветности, то что помешало бы им следовать его расчётам?
С другой стороны, это доказывает что на выходе из призмы действительно имеет место не разложение, а преобразование света. Если бы луч света уже представлял смесь, то не могло бы иметь места преобразование.
Благодаря расчётам Ньютона, в этой статье не только найдено ранее неизвестное свойство солнечных лучей, но и одновременно получено подтверждение этого свойства, которое не так легко было бы получить экспериментально.
Кроме того, мы осознали, что закон Снелля всегда правильный, так как он основан на эксперименте. Но, оказывается, не всё, что кажется нам преломлением, является им .
Но возможно, самым значительным результатом «анализа расчётов Ньютона», является то, что мы ещё раз убеждаемся в том, что расчёты никогда не могут заменить эксперимента и что физические законы никогда не следует пытаться открывать с помощью математики. Математика может быть царицей только в своей собственной области. В области физики или других наук математика должна быть «на подхвате».
Не может быть математической физики. Но может быть прикладная математика.
Литература
- Йохан Керн.Нет ничего более ошибочного, чем то, чему все верят (Легковерный Ньютон, или как свет разлагается призмой)
- Йохан Керн.Свет и кажущиеся явления
- Йохан Керн.Всегда ли «Каждый Охотник Желает Знать Где Сидит Фазан»?
- https://portal.tpu.ru/SHARED/s/SIB/Spisok/Tab/коэффициент.pdf , стр. 60-я.
- С.И. Вавилов. Исаак Ньютон http://vivovoco.ibmh.msk.su/VV/BOOKS/NEWTON/
- Йохан Керн. Мифы о ходе лучей в треугольной призме и новое представление о природе света
- Йохан Керн. Ошибка в оптике через 3 века породила ошибку в астрономии