Йохан Керн. Чем проще ошибка, тем труднее её заметить. Ошибка Гюйгенса-физика или Гюйгенса-математика?

При теоретическом объяснении огибания светом препятствий, разумеется, не обошлось без Гюйгенса. Как же, ведь он был к тому времени автором волновой теории света. Поэтому он и к вопросу огибания светом препятствия подошёл с тех же позиций.

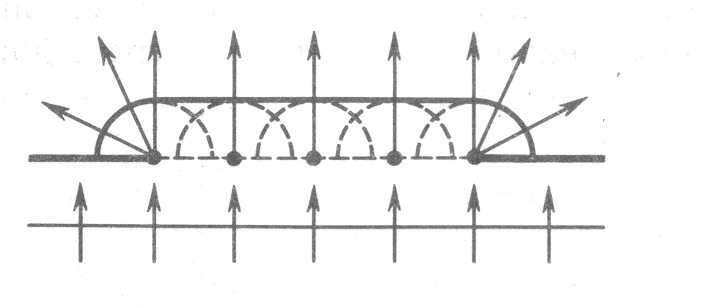
Взглянем на (Рис. 1) [1] (по Гюйгенсу). Пояснение принципа. Здесь отверстие образовано в стенке, не имеющей толщины. Поэтому края отверстия — это точки. Точка имеет площадь, равную нулю. Разумеется, никакой волны нулевая площадь отразить не может, или, другими словами, мощность отражённой волны будет равна нулю. То есть, никакого волнового «загиба» здесь быть не может. Все волны сквозь подобное отверстие могут распространяться только прямолинейно.

Любой математик, а тем более физик, должен был бы понять, что эта схема для «загиба лучей или волн» работать не может. Причём не только с волновой точки зрения, но и с корпускулярной.

Мы имеем право на абстракцию, на упрощение. Упрощение обычно помогает более ясно представить ситуацию. Но, как мы видим, и упрощение должно иметь свои пределы.

Рис. 1. Принцип Гюйгенса и объяснение затекания света в область геометрической тени

При этом Гюйгенс, как и в случае с прохождением света через призму, пренебрёг возможностями «корпускулярной» теории [2]. Мы же, как и в статье [2], попробуем посмотреть на огибание светом препятствия с точки зрения «корпускул», частичек света.

На рис. 2 показано отверстие (или щель) в «толстой» стенке, ограниченное линиями BACD и B'A'C'D'. Два параллельных луча света FE и F'E' (изображающие траекторию полёта «корпускулы», частички света) отражаются от края отверстия в точках E и E' и уходят далее в направлении EG и E'G'в область тени за отверстием. Нетрудно понять, что множество подобных параллельных лучей света совместно с параллельными лучами, проходящими в отверстие без соприкосновения с краями отверстия, образуют за отверстием пятно света с максимумом яркости напротив центра отверстия.

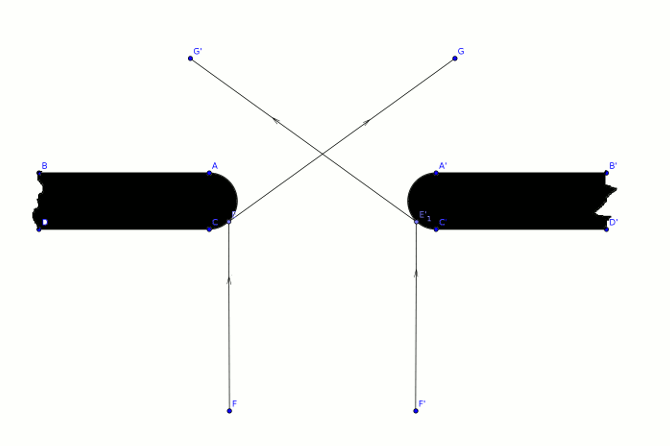
Рис. 2. Вхождение лучей света (или частичек) в область тени за отверстием или щелью.

Взглянем теперь на этот рисунок с волновой точки зрения. Каждую точку E или E' можно считать центром возникновения новой волны. При этом очевидно, что границей распространения волны из точки E или E'является касательная, проходящая через точку E или E'к полуокружностям, ограничивающим отверстие. За пределами касательной волна распространиться не может. Следовательно, волны, движущиеся параллельно линиям FE и F'E' и отразившиеся от правого края отверстия, могут распространяться только влево от отверстия, а волны от левого края — только вправо от отверстия.

То есть, в обоих случаях, как для волн, так и для частиц, мы имеем проникновение света в область «тени», в область, не освещаемую прямыми лучами.

Из рассмотрения этого рисунка можно понять и то, что свет, отражающийся от препятствия в виде одиночного тела, никак это тело обогнуть не может. Если же свет в действительности всё-таки огибает одиночное тело, то это должно объясняться из каких-то других соображений.

На помощь ошибочному рисунку приходит мистика
Им тоже план давай, хоть удавись.
В. Высоцкий

Уже Гюйгенс не обошёлся без мистики. Взгляните, на линию между краями отверстия (рис. 1). Здесь отражение волн происходит от несуществующих препятствий в виде точек.

Но во времена Гюйгенса и Френеля, похоже, было необходимо во что бы то ни стало объяснить, как свет может огибать препятствия. Гюйгенсу, „объяснившему“ на основе волновой теории разложение света на цветовые составляющие, хотелось на основе этой же теории объяснить и огибание светом препятствия. Он предположил, что точка может излучать волны, и на свет явился рис. 1, который, казалось, решал все проблемы.

В его время уже было известно дифференциальное и интегральное исчисление. Гюйгенс должен был бы понимать, что точка, обладающая нулевой поверхностью, ничего излучить не может. Для излучения необходима некая ненулевая площадь (сравните с рис.2). Но, похоже, когда существует острая необходимость, и математики и физики забывают применить веления логики и решают некоторые проблемы «на глазок». «На глазок» рис. 1 кажется убедительным.

Заметим, что некоторые авторы утверждают [1], что схема Гюйгенса неприменима для вычислений. Уж не потому ли, что площадь точки равна нулю?

Френель пошёл ещё дальше. Он применил мысленный волновой фронт и излучение волн из точек волнового фронта, не привязанного к какой-либо реальной поверхности. Это уже не математическая ошибка, это чисто мистический метод. Насколько мне известно, никто никогда не наблюдал излучения волн от поверхности, не являющейся разделом двух сред. В источнике [3] его идеи предлагают применить следующим образом. По рис. 3 мы имеем источник света S и диск (зачернённый прямоугольник), мешающий прямому распространению света из точки S в точку B. Автор источника говорит:

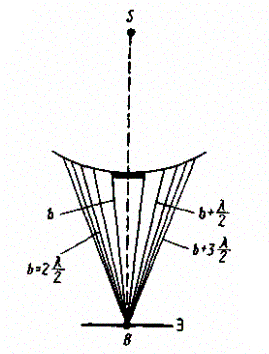
Рис. 3. Распространению света из точки S (Рис. 260 из [3])

«В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска». То есть, начиная с мысленной, ничему реальному не соответствующей поверхности?

Френель был очень талантливым человеком. Одна только линза Френеля может увековечить его имя. Но это вовсе не означает, что из-за этого надо верить и его мистическим идеям.

К сожалению, ничем нельзя обосновать подобные идеи. Они кажутся соглашательством.

Разумеется, мне известно, что на этом «пути» достигнуты «большие успехи» в области объяснения дифракции и спектроскопии. Но точно также когда-то астрономы успешно и с большой точностью рассчитывали затмения Луны и Солнца, а также движения планет по небосводу, имея очень превратное понимание устройства солнечной системы.

Волновое «объяснение» разложения света призмой служило доказательством волновой природы света. Огибание светом препятствия объясняли, считая волновую природу света доказанной. В этом случае было бы правомерным и разбиение светового фронта на зоны Френеля (Рис. 3), исходя из точки наблюдения. Но световой фронт при этом обязательно должен соответствовать некоторой реальной поверхности. Волна не может исходить из точки пространства, не лежащей на поверхности преграды.

Поверим на минутку мистической идее Френеля и поместим на рис. 1 несколько мысленных «точек отражения волн» за линией, соединяющей края отверстия. Эти точки бнудут отражать волны во всех направлениях, в том числе и в обратную сторону. Отсюда следует, что свет должен бы освещать и обратную сторону поверхности, в которой находится отверстие. Но вот этого точно никто никогда не видел, или?

Следовательно, точки отражения Френеля надо помещать только так, чтобы была возможность получить желаемый результат. А это ничто иное, как метод подгонки. Так можно «доказать» всё, что угодно, в том числе и существование бога.

Из рис. 2 становится понятным, что свет может попасть в пространство геометрической тени за отверстием. Но он никак не может попасть в область геометрической тени какого-либо одиночного предмета, не имеющего сквозного отверстия или сквозной щели. Ни волновая природа света, ни корпускулярная этому помочь не могут. Если свет и попадает за преграду, то этому должно быть иное (теоретическое) объяснение.

Ссылки

Знаете ли Вы, что "тёмная материя" - такая же фикция, как черная кошка в темной комнате. Это не физическая реальность, но фокус, подмена.
Реально идет речь о том, что релятивистские формулы не соответствуют астрономическим наблюдениям, давая на порядок и более меньшую массу и меньшую энергию. Отсюда сделан фокуснический вывод, что есть "темная материя" и "темная энергия", но не вывод, что релятивистские формулы не соответствуют реалиям. Подробнее читайте в FAQ по эфирной физике.