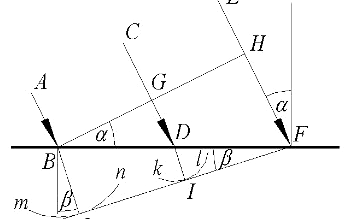
Рис. 1. Ход лучей при преломлении света на границе
двух сред можно получить без предположения,
что свет распространяется подобно волне.
Йохан Керн / Johann Kern, Stuttgart, jo_k@gmx.net (31/10/2003)
В статье обсуждаются заблуждения, основанные на математике. Высказывается мнение, что новые законы природы невозможно получить с помощью математики, без опоры на опыт.
Когда-то философию называли царицей наук. Причиной этого было скорее всего то, что философия древности объединяла в себе все науки. Наука о (неживой) природе, когда она несколько обособилась от общей философии, стала называться натуральной философией. Из неё возникли физика, механика и мн. др. технические науки. Другими словами, философия когда-то была единственной наукой.Об этом говорит и само слово философия, произошедшее из двух греческих слов: любить + мудрость. Главным достоинством философа было умение рассуждать, обосновывать. При этом ему помогало знание логики. Нелогичное рассуждение легко опровергнуть. Логика нужна везде. От логики происходит разумность, логичность поведения. Мы её применяем на каждом шагу, даже не замечая этого. Например, стараясь срезать прямой угол. Как и во многом другом, въевшаяся в кровь и плоть последовательность поведения доводит порой до абсурда: срезать угол мы неосознанно пытаемся и во время прогулок. Логика вполне могла бы объявить себя главной из наук. Но эта наука обладает врождённой скромностью. Она скорее всего претендует быть слугой, помощницей для всех, никогда не напоминая о своих заслугах.
Математика же - это наука о вычислениях. Она помогала точно выразить свою мысль о величине чего-либо: площади, расстоянии, величине отрезка времени. То есть она была всегда наукой прикладной, вспомогательной, находившей применение в различных областях человеческой деятельности, часто в очень приземлённых, как, например, в бухгалтерии. Но, слуга по призванию, математика действует по принципу: плох тот солдат, который не хочет стать генералом. Математика не однажды хотела объявить себя самой главной наукой, без которой дальнейшее продвижение вперёд просто невозможно. Впервые это произошло в астрономии. Любой астроном должен хорошо знать математику, должен хорошо уметь вычислять. Но астрономия основана на опыте наблюдения. Поэтому сперва и астрономы тоже всё делали более или менее на глазок. В те времена возникла система Птолемея: Земля находилась в центре мироздания, вокруг на хрустальных сферах вращались планеты и Солнце, далее находилась сфера неподвижных звёзд. Но всё более точное наблюдение планет и фиксация этих движений вскоре привело к появлению первого кризиса в астрономии. Выяснилось, что планеты делают странные движения. Они вдруг ни с того, ни с сего останавливались при своём движении по «небосводу» и даже начинали двигаться в обратную сторону. Это казалось совершенно необъяснимым. Положение «спас» математик, предложивший считать, что центры планетных сфер совершают вращательное круговое движение вокруг своего центра вращения. Необходимость нарушения простоты божественного механизма мироздания он разумно объяснить не мог, но наложение уже одного дополнительного вращательного движения сильно улучшало точность предсказуемости положения планеты. Требования к математической квалификации астрономов соответственно возросли. Вскоре выяснилось, что наложение ещё одного вращательного движения позволяет ещё более точно определить положение планет. Всё большее улучшение средств наблюдения требовало введения новых и новых дополнительных вращательных движений.
Бог, как и гений, должен делать всё очень просто. Осмысленность такого сложного «божественного» механизма становилась всё менее объяснимой. Астрономия двигалась в тупик. Но математики чувствовали себя в астрономии всё более незаменимыми. Только они могли объяснить столь сложный механизм и (достаточно) точно рассчитать его поведение.
Выход из тупика предложил человек, бывший не столько математиком, сколько астрономом, может быть даже, по современным понятиям, физиком. Он предложил считать центром Вселенной Солнце. Но так как и он был человеком своего времени, то и он считал, что планеты должны двигаться (вокруг Солнца) по круговой траектории, причём, конечно, равномерно. Основания думать иное тогда ни у кого не было. Помещение Солнца в центре мироздания объясняло петлеобразное движение планет, но большой точности предсказаний (вычислений) положения планет не давало. Именно поэтому приверженцы системы Птолемея благоденствовали ещё даже во времена Ньютона. Медленное умирание системы Птолемея привело к тому, что своего фиаско в попытке математически объянить устройство мироздания математика, кажется, так и не осознала. Тем более, что Ньютон, окончательно проведший черту под системой мироздания по Птолемею, был не только великим физиком (натурфилософом!), но и великим математиком. Он представил новое, чудесно простое устройство мироздания благодаря своему закону о всемирном тяготении. Математики, причём гораздо более высокой квалификации, понадобились и новой системе мироздания. Но чем было новое объяснение мироздания - новым торжеством математики или же успехом физики (натурфилософии)?
Мысль о существовании всемирного тяготения могла возникнуть при наблюдении падающего яблока. Нарисовав земной шар с яблоней и яблоком, мы, поворачивая рисунок вокруг земного шара, можем понять, что яблоко не падает, а притягивается к Земле, к земному шару. Зная третий закон Ньютона - действие равно противодействию, мы можем догадаться, что не только яблоко притягивается к Земле, но и Земля притягивается к яблоку. Ещё больше обобщив ситуацию, мы можем догадаться, что - все тела притягиваются друг к другу, т.е. получить закон всемирного тяготения. Но такие умные мы можем быть сейчас, когда этот закон давным давно известен. В действительности человечеству для этого понадобились тысячелетия, если не говорить - миллионы лет.
Закон всемирного тяготения: «все тела притягиваются друг к другу» - звучит совсем не математически. Это утверждение философа, натурфилософа, физика. Да и доказать мы ничего не доказали - мы просто догадались. Доказать это утверждение невозможно. Ньютону окончательно поверили только через сто с лишним лет, когда Кавэндиш с помощью изобретённых им крутильных весов смог доказать экспериментально, что два свинцовых шара притягиваются друг к другу, т.е. он сумел измерить силу притяжения этих шаров. Но и это, формально говоря, не является доказательством закона всемирного тяготения. Из того, что два тела А и В притягиваются друг к другу, вовсе не следует, что и тело С также будет притягиваться к каждому из этих тел. Но таковы люди: стоит нам увидеть, что две реки текут вниз, как мы уже уверяем, что все реки текут вниз. Именно поэтому астрономы говорят, что по их сведениям на таком то расстоянии от нас закон всемирного тяготения всё ещё подтверждается. То есть, он не доказан.
Другими словами, физический закон - это то, чему мы верим на основе многих примеров, на основе нашего опыта. Но толкование опыта может быть ошибочным. Именно поэтому некоторые физические законы время от времени в корне меняют свою формулировку. Например, закон инерции, который со времён Галилея звучит примерно так: тело двигается прямолинейно и равномерно до тех пор, пока на него не подействует сила, во времена древних греков и вплоть до времён Галилея звучал совсем по другому: тело двигается (прямолинейно и равномерно) до тех пор, пока на него действует сила. И поверьте, у древних греков были основания для подобного утверждения. Но Галилей сумел доказать (убедить своих современников), что греки заблуждались.
Но, может быть, плодом математики является «математическая формулировка» закона всемирного тяготения? Однако она говорит не о всех, а только о двух телах. Притяжение в известном смысле изучал ещё Галилей, причём экспериментально, как физик, и он установил, что все тела падают на землю с одинаковым ускорением. А так как он установил экспериментально и так называемый первый закон Ньютона F = ma, где F - сила, действующая на тело с массой m, а a - ускорение тела, то ещё Галилей мог сказать, что падающее тело притягивается к Земле с силой, пропорциональной массе тела m. Из аналогии мы можем сказать, что Земля притягивается к телу с силой, пропорциональной своей массе M. Из третьего закона Ньютона мы знаем, что эти силы равны друг другу, а из этого следует, что они должны содержать сомножителями как m, так и M, т.е. сила притяжения между двумя телами пропорциональна произведению их масс. Итак, мы ещё ничего не вычисляли, а уже почти получили формулу притяжения между двумя телами. Осталось показать, что эта сила будет обратно пропорциональна квадрату расстояния, но ещё до Ньютона было известно, что притяжение между двумя небесными телами обратно пропорционально квадрату расстояния. То есть, ни один элемент формулы тяготения в известном смысле не являлся продуктом применения математики. Но самое главное здесь - необходимость применения закона о пропорциональности ускорения силе, который можно обосновать только экспериментально. Из одного знания математики формулу притяжения никак не выведешь. Но почему же Ньютона так хвалили тогда именно как математика? А потому, что применив уже полученную им формулу тяготения, он чисто математически (посредством вычислений) показал, что эта формула позволяет объяснить многие явления, бывшие до того непонятными, например, приливы и отливы. Таким образом, математика играла в этом процессе важную, но чисто вспомогательную роль, и служила своему прямому назначению - вычислениям.
Можно ли вообще чисто с помощью математики доказать наличие какого-либо свойства у вещества, о котором мы раньше не предполагали или в котором раньше не были уверены? «Конечно, можно, - скажет сведущий читатель. - Например, Гюйгенс, современник Ньютона, с помощью очень простого и изящного математического метода доказал волновые свойства света. Он этим посрамил тогда самого Ньютона, считавшего свет потоком частиц». Это верно. Доказательство очень простое, и, как все тогда считали, без сучка и задоринки.
|
Рис. 1. Ход лучей при преломлении света на границе |
Но закон преломления света, теоретически объяснённый тогда Гюйгенсом, можно получить и несколько проще и без предположения, что мы имеем дело с волновым явлением. Возьмём три параллельных луча света AB, CD и EF в одной плоскости и на равном расстоянии друг от друга (рис. 1). Проведём перпендикуляр ВР к этим лучам и предположим, что в некоторый момент времени t = 0 эти три луча как раз достигли перпендикуляр ВР в точках B, G и H. Точка B при этом одновременно принадлежит прямой BF, являющейся линией раздела между двумя оптическими средами, например, между воздухом и водой. В момент времени t = 1 луч CD также достигнет линию раздела сред BF в точке D. Через вдвое больший отрезок времени, в момент t = 2, линию раздела BF достигнет и луч EF в точке F. Луч же CD в момент времени t = 1 преломится на границе раздела сред в точке D и к моменту времени t = 2 пройдёт в более плотной среде расстояние до дуги kl. (Радиус дуги kl меньше расстояния между точками G и D, которое луч прошёл за то же время, так как скорость движения в более плотной среде меньше, чем в воздухе.) Луч же AB преломится на границе раздела сред в точке B уже в момент времени t = 0 и к моменту времени t = 2 пройдёт в более плотной среде вдвое большее расстояние до дуги mn. Чтобы определить направление движения лучей в более плотной среде, мы проведём из точки F касательную к дугам kl и mn, которая коснётся дуг в точках I и J. Прямые DI и BJ дадут направление движения лучей в более плотной среде. Они параллельны друг другу, так как все параллельные лучи преломляются одинаково. Они перпендикулярны линии FJ, так как линия FJ является касательной. (Концы параллельных лучей из точек B и D до дуг kl и mn лежат на одной и той же секущей из точки F ввиду подобия получаемых треугольников. Но каждая секущая даёт два возможных направления лучей. Направление же может быть только одно. Поэтому можно учитывать только направление лучей, даваемое в точке пересечения с касательной).
Таким образом, мы получили ход лучей, не ставя никаких требований к лучам света, за исключением вполне естественных: скорости всех лучей (одного цвета) внутри одной среды одинаковы. По нашему рисунку величины лучей GD и DI соответствуют скорости света в одной из сред, т.е. GD = V1, а DI = V2. Назвав теперь угол DBG углом α, а угол IFD углом ß, мы получим V1 = BD sin α и V2 = FD sin ß, откуда, учитывая, что BD = FD, следует:
sin α /sin ß = V1 / V2.
где α - угол падения лучей, а ß - угол преломления. Мы получили закон преломления лучей света на границе двух сред, но при этом не можем утверждать, что свет обладает волновыми свойствами.
Если мы теперь вспомним построение Гюйгенса [1], то увидим, что рисунки чем-то похожи, за тем исключением, что Гюйгенсу понадобилось рисовать очень много дуг, а нам только две. Не опрерировал ли и Гюйгенс на самом деле со скоростями света в средах, а вовсе не с волнами? Посмотрим внимательно на построение Гюйгенса. Мы можем заметить, что передача «воздействия волны» происходит только в одном направлении, без обратного взаимодействия частиц, которое должно было бы иметь место в процессе колебаний, в процессе волнового воздействия. Рисунок только похож на изображение волны, на самом деле это односторонний последовательный перенос (через одни и те же промежутки) монотонной последовательности точек. Скорость, помноженная на определённый промежуток времени, это определённое расстояние. Вглядитесь ещё раз в рисунок: Гюйгенс, как и мы, оперировал только со скоростью движения света (в единицу времени), а вовсе не с волной! Мы убеждаемся, что Гюйгенс, как и все математики при решении физических проблем, ошибся в самом начале. Гениальный Ньютон, как и все остальные (все мы только человеки), повидимому, поддался гипнозу правильного результата и не стал проверять ход рассуждений Гюйгенса, иначе бы он заметил, что доказательство Гюйгенса не имеет ничего общего с колебательным движением, присущим волне. Он вполне мог щелчок, полученный им от Гюйгенса, передать ему обратно. В то время это могло сильно повлиять на ход развития физики.
Но ведь Гюйгенс всё-таки получил правильное значение для скорости света в более плотной среде, которое тогда никому не было известно? Да, получил. Он взял большее и меньшее значение для скорости света и убедился, что практике (величине известного угла преломления) соответствует только меньшее значение скорости. Без сравнения с известным ранее экспериментальным результатом угла преломления и известной формулой для угла преломления его математические изыскания были бы пустым фантазированием. То есть, и этот пример показывает, что математика, как правило, ничего не может объяснить, а может только уточнить.
Не создалось ли у читателя впечатление, что автор пытается внушить ему, что с помощью математики уж что-что, а нового закона физики не вычислишь, т.е. не докажешь? Это было бы со стороны автора явно неосторожным. Ведь существует теория относительности (ТО), разработанная Эйнштейном чисто теоретически, без опоры на результаты эксперимента. Разве не были получены на её основе сногсшибательные результаты, можно сказать, новые физические законы, противоречащие всей тогдашней практике?
Вот именно, противоречащие. Но не во всём. Эйнштейн написал эту работу с целью объяснить (отрицательный) результат экспериментов Майкельсона, и этого, как ему показалось, он достиг. К сожалению, как раз в момент своего кажущегося успеха он находился в деформированной системе координат. Успешное теоретическое подтверждение практики (результата экспериментов Майкельсона), повидимому, слегка вскружило ему голову и он забыл, что любые результаты надо рассматривать в реальной системе координат. В деформированной же системе координат, естественно, и выводы выглядят несколько деформированно [2]. Полученные «результаты», не считая «подтверждения» результатов экспериментов Майкельсона, его самого очень удивили и он назвал их «своеобразными» [3]. Однако своеобразие полученных результатов почему-то не побудило его тщательно перепроверить всю свою работу от начала до конца.
Но самое удивительное в истории с ТО состоит, наверное, в том, что её многочисленные противники, появившиеся сразу после появления ТО, похоже, не заметили этой, в общем-то банальной, ошибки Эйнштейна, полностью обесценивающей все его результаты, а пытались доказать нелогичность его выводов. Обширный список противников Эйнштейна и названия их работ читатель может найти в очень интересной книге [4].
Кажущийся успех побудил Эйнштейна продолжить поиск чисто математических объяснений физических феноменов. В этот раз он решил объяснить гравитацию - с помощью «кривизны пространства». В связи с этим нам надо оживить в памяти, что такое кривизна и что может быть кривым. Газ полностью заполняет любой самой причудливой формы объём, но вряд-ли кому придёт в голову сказать, что газ может быть кривым. То же самое, очевидно, нельзя сказать и о жидкости, хотя она заполняет только нижнюю часть объёма. Кривым или имеющим свою собственную форму может быть только (относительно) твёрдое тело. От помещения в сосуд оно форму практически не меняет. Другими словами, чтобы быть кривым (иметь кривизну), тело или вещество должно быть связным, соседняя частичка связного вещества не может отдаляться от своей соседки слишком далеко, иначе будет нарушена связь. Кроме того, связное тело допускает движение только вдоль своей границы, но никак не внутри себя. В этом смысле ни газ, ни жидкость не являются связными: их частички могут как угодно далеко смещаться относительно друг друга, внутри этих сред можно перемещаться, их свойства от этого не меняются. Твёрдое тело может быть кривым или приобретать кривизну в напряжённом состоянии. Через твёрдое тело ничто не может пройти без нарушения связи части его частиц. Пустое пространство не содержит частиц, не может быть связным, а потому и не может быть кривым. Что же отсюда следует? Похоже на то, что «пустое» кривое пространство Эйнштейна заполнено самым невероятным из всех придуманных до сих пор эфиров - твёрдым веществом. А двигаться внутри твёрдого вещества без нарушения его связей могут разве что только математики.
Если мы не сделали никакой логической ошибки (сторонники Эйнштейна наверняка скажут, что в 4-х-мерном связном пространстве вполне можно свободно перемещаться), то мы нашли вескую причину, почему в пределах и этой теории Эйнштейна происходят всякие чудеса - она нереальна, оторвана от практики. Оторвана по той причине, что Эйнштейн даже не пытался развить или хотя бы объяснить какой-либо реальный факт, связанный с тяготением - он всё высосал из пальца, также, как и теорию относительности, не считаясь с тем, что кривого вакуума быть не может.
Но нет худа без добра. Идеи Эйнштейна подхватили многочисленные писатели-фантасты. Для них он стал неисчерпаемым колодцем новых сюжетов.
Конечно, мы не доказали строго, что с помощью одной лишь математики нельзя доказать (найти) нечто принципиально новое в физике. Но мы посеяли сомнение. Мы привели только данные человеческого опыта. А это не является доказательством. Мы показали, что с помощью математики мы можем успешно вводить себя в заблуждение, получая, казалось бы, очень простое и убедительное доказательство чего-либо. Точно также во времена существования системы Птолемея математики успешно убеждали нас и были убеждены сами в том, что они знают, что делают. А не знали и не понимали.
Разумеется, целью этой статьи не является попытка занизить заслуги математики. Они огромны, в том числе и в области физики. Исследуя равенства и уравнения, выражающие связь между физическими величинами, математики внесли огромный вклад в развитие науки и техники. Но математика не должна пытаться решать проблемы, не присущие ей, не должна пытаться открывать физические законы посредством вычислений, не делать слишком далеко идущие выводы. Наши знания ограничены, известные нам зависимости отражают природу , как правило, только приближённо, поэтому далеко идущие выводы надо делать с крайней осторожностью. Например, решая уравнения, относящиеся к области метеорологии, математики пришли к очаровывающему, но смехотворному выводу, что взмах крыла бабочки в Средней Азии может привести к урагану в Америке. К подобному эффекту не может привести даже многочасовая дружная работа целой эскадрильи военных вертолётов или, скажем, запуск многотонной ракеты в Байконуре. Если математик пришёл к настолько «своеобразному» выводу, что он начинает по эффектности напоминать выводы ТО, то он должен немедленно начать искать допущенную им ошибку. Но, разумеется, не тогда, если хочет скандально прославиться.
Конечно, нельзя потребовать, чтобы математики не занимались (самостоятельно) физикой. Но ведь дело доходит до обратного, до утверждения, что развитие физики невозможно без математики. Прикладная физика чаще всего невозможна без математики. Толкование физических фактов полезно подкрепить вычислениями. Но вычисления - только внешняя сторона дела. Платье не делает короля. Платье делает только марионетку. Конечно, и от физика нельзя требовать, чтобы он обходился без вычислений. Вычисление - это использование математики как инструмента. Использование же математики для создания физических теорий, не имея в основе уравнений, связывающих физические величины - это мания всемогущества математики. Пример этому, безусловно, прежде всего ТО, приведшая к действительно маниакальным результатам [2]. Более безобиден широко распространённый метод рассматривания частицы в потенциальной яме. Ничего нового при этом не получают, кроме уже известной величины вероятности какого-либо события, но выражают чрезвычайно умными словами уже известное. От потенциальной ямы рукой подать до «туннельного перехода», в котором очень импонирующим математическим языком выражена простая мысль: «Не знаю, как это получается, но эта частица всё время выскакивает из этой глубокой потенциальной ямы». Но ведь скажи так - и научного звания не получишь. А вырази свою беспомощность на не всем понятном языке туннельного перехода - и отсутствие успеха превращается в успех!
Математики всегда помогают физикам утвердиться в своих заблуждениях. Выход из тупика физики всегда должны найти сами. В подтверждение этого не будем вспоминать Коперника, а возьмём менее известный случай заблуждения, связанный с большой луной на горизонте, которая всем так нравится. Беспомощный физик обратился во времена Снеллиуса к матеметику с идеей, что здесь, наверно, виноват более толстый слой атмосферы, который световой луч должен пройти по касательной к земному шару, в результате чего луч имеет гораздо большее преломление. Математик быстренько нарисовал соответствующую схему, всё вычислил и этим подтвердил идею физика. Это объяснение потом во славу науки перекочевало во все учебники физики. Математик, конечно, не заметил, что это объяснение могло относиться только к вертикальному диаметру луны, но никак не к горизонтальному. Луна должна была бы получиться эллиптической.
Несколько позже народный умелец и немного физик закоптил простое стекло и посмотрел сквозь него на большую луну. Яркая луна была видна сквозь тёмное стекло, но линия горизонта исчезла. И - о, чудо! - луна приобрела самые обычные нормальные размеры. Стало ясно, что большая луна не имеет прямого отношения к физике, а разве что к физике нашей психики. Пример этот не мог добавить славы науке и малоизвестен до сих пор.
Кто здесь виноват? Физик или математик? Конечно, оба. Но математик не помог физику преодолеть своё заблуждение, не оказался «мыслителем», на роль которого претендует.
В наше время физика становится всё более математизированной. Представление какого- либо физического процесса без обилия математических формул кажется франтам от науки, жонглёрам от математики, ущербным. Скатывания же к откровенной мистике они не замечают. Возьмём так называемую квантовую физику. Она безусловно является достойной преемницей системы Птолемея. Уже много лет тому назад она отказалась от детерминизма, от взаимосвязи причины и следствия - и этим начала двигаться к новому тупику. Кто-нибудь делает голословное утверждение типа «Планета находится на поверхности хрустальной сферы» - и все начинают её повторять. Электрон не имеет орбиты, а образует электронное облако вокруг ядра. Это ещё можно было бы представить как своего рода приближение или осреднение, но нет, прямо утверждается, что электрон не перемещается от одной точки к другой, а появляется то тут, то там, минуя промежуточные положения! Таким образом решили исключить колебательные движения электрона, т.е. избежать излучения энергии электроном при образовании электронного облака. Вот уж поистине - из огня да в полымя! Это решение равносильно предложению: «Давайте не будем называть колебания колебаниями!» Разумеется, никто не может объяснить, как это электрон может появляться то тут, то там, минуя промежуточные положения. Появляется - и всё тут! К этой же области «науки» относится и появление различного рода частиц из вакуума, к тому же ешё и беспричинное. Не наука, а чертовщина. Точно такой же степени обоснованности, как были «обоснованы» не только небесные сферы в системе Птолемея , но и все эти бесчисленные дополнительные вращательные движения. Как тогда эта бессмыслица или произвольность привела со временем к падению системы Птолемея, так и теперь она приведёт к падению «квантовой механики». Но попробуйте это объяснить современному математику, мнящему себя физиком, насквозь заражённому мистикой квантовых и магических чисел, «разрешёнными орбитами» и прочими атрибутами колдовских учебников. После этого «проколы» пространства-времени и путешествие во времени становятся чуть ли не материализмом.