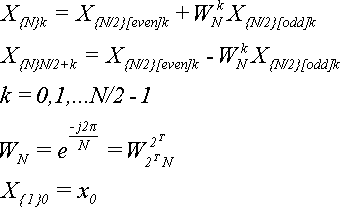(16) Подведем итог:
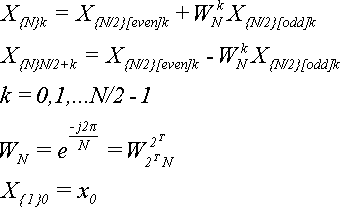(16)
Теперь рассмотрим конкретную реализацию БПФ. Пусть имеется N=2T элементов последовательности x{N} и надо получить последовательность X{N}. Прежде всего, нам придется разделить x{N} на две последовательности: четные и нечетные элементы. Затем точно так же поступить с каждой последовательностью. Этот итерационный процесс закончится, когда останутся последовательности длиной по 2 элемента. Пример процесса для N=16 показан ниже:
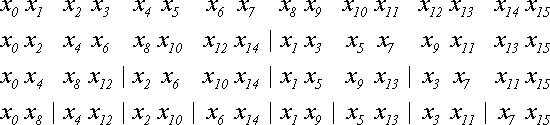
Итого выполняется (log2N)-1 итераций.
Рассмотрим двоичное представление номеров элементов и занимаемых ими мест. Элемент с номером 0 (двоичное 0000) после всех перестановок занимает позицию 0 (0000), элемент 8 (1000) - позицию 1 (0001), элемент 4 (0100) - позицию 2 (0010), элемент 12 (1100) - позицию 3 (0011). И так далее. Нетрудно заметить связь между двоичным представлением позиции до перестановок и после всех перестановок: они зеркально симметричны. Двоичное представление конечной позиции получается из двоичного представления начальной позиции перестановкой битов в обратном порядке. И наоборот.
Этот факт не является случайностью для конкретного N=16, а является закономерностью. На первом шаге четные элементы с номером n переместились в позицию n/2, а нечетные из позиции в позицию N/2+(n-1)/2. Где n=0,1,…,N-1. Таким образом, новая позиция вычисляется из старой позиции с помощью функции:
ror(n,N) = [n/2] + N{n/2}
Здесь как обычно [x] означает целую часть числа, а {x} - дробную.
В ассемблере эта операция называется циклическим сдвигом вправо (ror), если N - это степень двойки. Название операции происходит из того факта, что берется двоичное представление числа n, затем все биты, кроме младшего (самого правого) перемещаются на 1 позицию вправо. А младший бит перемещается на освободившееся место самого старшего (самого левого) бита.
рис. 1
Дальнейшие разбиения выполняются аналогично. На каждом следующем шаге количество последовательностей удваивается, а число элементов в каждой из них уменьшается вдвое. Операции ror подвергаются уже не все биты, а только несколько младших (правых). Старшие же j-1 битов остаются нетронутыми (зафиксированными), где j - номер шага:
рис. 2
Что происходит с номерами позиций при таких последовательных операциях? Давайте проследим за произвольным битом номера позиции. Пусть этот бит находился в j-м двоичном разряде, если за 0-й разряд принять самый младший (самый правый). Бит будет последовательно сдвигаться вправо на каждом шаге до тех пор, пока не окажется в самой правой позиции. Это случится после j-го шага. На следующем, j+1-м шаге будет зафиксировано j старших битов и тот бит, за которым мы следим, переместится в разряд с номером T-j-1. После чего окажется зафиксированным и останется на месте. Но именно такое перемещение - из разряда j в разряд T-j-1 и необходимо для зеркальной перестановки бит. Что и требовалось доказать.
Теперь, мы убедились в том, что перестановка элементов действительно осуществляется по принципу, при котором в номерах позиций происходит в свою очередь другая перестановка: зеркальная перестановка двоичных разрядов. Это позволит нам получить простой алгоритм:
for(I = 1; I < N-1; I++)
{
J = reverse(I,T); // reverse переставляет биты в I в обратном порядке
if (I >= J) // пропустить уже переставленные
conitnue;
S = x[I]; x[I] = x[J]; x[J] = S; // перестановка элементов xI и xJ
}
Некоторую проблему представляет собой операция обратной перестановки бит номера позиции reverse(), которая не реализована ни в популярной архитектуре Intel, ни в наиболее распространенных языках программирования. Приходится реализовывать ее через другие битовые операции. Ниже приведен алгоритм функции перестановки T младших битов в числе I:
unsigned int reverse(unsigned int I, int T)
{
int Shift = T - 1;
unsigned int LowMask = 1;
unsigned int HighMask = 1 << Shift;
unsigned int R;
for(R = 0; Shift >= 0; LowMask <<= 1, HighMask >>= 1, Shift -= 2)
R |= ((I & LowMask) << Shift) | ((I & HighMask) >> Shift);
return R;
}
Пояснения к алгоритму. В переменных LowMask и HighMask хранятся маски, выделяющие два переставляемых бита. Первая маска в двоичном представлении выглядит как 0000…001 и в цикле изменяется, сдвигая единицу каждый раз на 1 разряд влево:
0000...001 0000...010 0000...100 ...
Вторая маска (HighMask) принимает последовательно значения:
1000...000 0100...000 0010...000 ...,
каждую итерацию сдвигая единичный бит на 1 разряд вправо. Эти два сдвига осуществляются инструкциями LowMask <<= 1 и HighMask >>= 1.
Переменная Shift показывает расстояние (в разрядах) между переставляемыми битами. Сначала оно равно T-1 и каждую итерацию уменьшается на 2. Цикл прекращается, когда расстояние становится меньше или равно нулю.
Операция I & LowMask выделяет первый бит, затем он сдвигается на место второго (<<Shift). Операция I & HighMask выделяет второй бит, затем он сдвигается на место первого (>>Shift). После чего оба бита записываются в переменную R операцией "|".
Вместо того чтобы переставлять биты позиций местами, можно применить и другой метод. Для этого надо вести отсчет 0,1,2,…,N/2-1 уже с обратным следованием битов. Опять-таки, ни в ассемблере Intel, ни в распространенных языках программирования не реализованы операции над обратным битовым представлением. Но алгоритм приращения на единицу известен, и его можно реализовать программно. Вот пример для T=4.
I = 0;
J = 0;
for(J1 = 0; J1 < 2; J4++, J ^= 1)
for(J2 = 0; J2 < 2; J3++, J ^= 2)
for(J4 = 0; J4 < 2; J4++, J ^= 4)
for(J8 = 0; J8 < 2; J8++, J ^= 8)
{
if (I < J)
{
S = x[I]; x[I] = x[J]; x[J] = S; // перестановка элементов xIи xJ
}
I++;
}
В этом алгоритме используется тот общеизвестный факт, что при увеличении числа от 0 до бесконечности (с приращением на единицу) каждый бит меняется с 0 на 1 и обратно с определенной периодичностью: младший бит - каждый раз, следующий - каждый второй раз, следующий - каждый четвертый и так далее.
Эта периодичность реализована в виде T вложенных циклов, в каждом из которых один из битов позиции J переключается туда и обратно с помощью операции XOR (В C/C++ она записывается как ^=). Позиция I использует обычный инкремент I++, уже встроенный в язык программирования.
Данный алгоритм имеет тот недостаток, что требует разного числа вложенных циклов в зависимости от T. На практике это не очень плохо, поскольку T обычно ограничено некоторым разумным пределом (16..20), так что можно написать столько вариантов алгоритма, сколько нужно. Тем не менее, это делает программу громоздкой. Ниже я предлагаю вариант этого алгоритма, который эмулирует вложенные циклы через стеки Index и Mask.
int Index[MAX_T];
int Mask[MAX_T];
int R;
for(I = 0; I < T; I++)
{
Index[I] = 0;
Mask[I] = 1 << (T - I - 1);
}
J = 0;
for(I = 0; I < N; I++)
{
if (I < J)
{
S = x[I]; x[I] = x[J]; x[J] = S; // перестановка элементов xI и xJ
}
for(R = 0; R < T; R++)
{
J ^= Mask[R];
if (Index[R] ^= 1) // эквивалентно Index[R] ^= 1; if (Index[R] != 0)
break;
}
}
Величина MAX_T определяет максимальное значение для T и в наихудшем случае равна разрядности целочисленных переменных ЭВМ. Этот алгоритм, может быть, чуть медленнее, чем предыдущий, но дает экономию по объему кода.
И, наконец, последний алгоритм. Он использует классический подход к многоразрядным битовым операциям: надо разделить 32-бита на 4 байта, выполнить перестановку в каждом из них, после чего переставить сами байты.
Перестановку бит в одном байте уже можно делать по таблице. Для нее нужно заранее приготовить массив reverse256 из 256 элементов. Этот массив будет содержать 8-битовые числа. Записываем туда числа от 0 до 255 и переставляем в каждом порядок битов.
Теперь этот массив применим для последней реализации функции reverse:
unsigned int reverse(unsigned int I, int T)
{
unsigned int R;
unsigned char *Ic = (unsigned char*) &I;
unsigned char *Rc = (unsigned char*) &R;
Rc[0] = reverse256[Ic[3]];
Rc[1] = reverse256[Ic[2]];
Rc[2] = reverse256[Ic[1]];
Rc[3] = reverse256[Ic[0]];
R >>= (32 - T);
Return R;
}
Обращения к массиву reverse256 переставляют в обратном порядке биты в каждом байте. Указатели Ic и Ir позволяют обратиться к отдельным байтам 32-битных чисел I и R и переставить в обратном порядке байты. Сдвиг числа R вправо в конце алгоритма устраняет различия между перестановкой 32 бит и перестановкой T бит. Ниже приводится наглядная геометрическая иллюстрация алгоритма, где стрелками показаны перестановки битов, байтов и сдвиг.
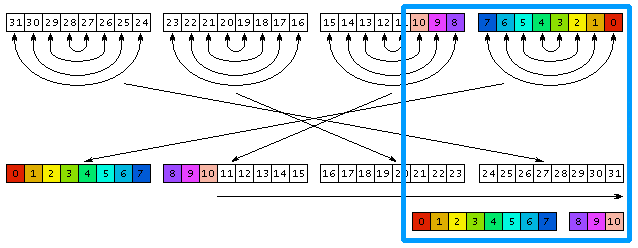
рис. 3
Оценим сложность описанных алгоритмов. Понятно, что все они пропорциональны N с каким-то коэффициентом. Точное значение коэффициента зависит от конкретной ЭВМ. Во всех случаях мы имеем N перестановок со сравнением I и J, которое предотвращает повторную перестановку некоторых элементов. Рядом присутствует некоторый обрамляющий код, применяющий достаточно быстрые операции над целыми числами: присваивания, сравнения, индексации, битовые операциии и условные переходы. Среди них в архитектуре Intel наиболее накладны переходы. Поэтому я бы рекомендовал последний алгоритм. Он содержит всего N переходов, а не 2N как в алгоритме со вложенными циклами или их эмуляцией и не NT как в самом первом алгоритме.
С другой стороны, предварительная перестановка занимает мало времени по сравнению с последующими операциями, использующими (N/2)log2N умножений комплексных чисел. В таком случае тоже есть смысл выбрать не самый короткий, но самый простой и наглядный алгоритм - последний описанный. Вот его окончательный вид с небольшой оптимизацией:
static unsigned char reverse256[]= {
0x00, 0x80, 0x40, 0xC0, 0x20, 0xA0, 0x60, 0xE0,
0x10, 0x90, 0x50, 0xD0, 0x30, 0xB0, 0x70, 0xF0,
0x08, 0x88, 0x48, 0xC8, 0x28, 0xA8, 0x68, 0xE8,
0x18, 0x98, 0x58, 0xD8, 0x38, 0xB8, 0x78, 0xF8,
0x04, 0x84, 0x44, 0xC4, 0x24, 0xA4, 0x64, 0xE4,
0x14, 0x94, 0x54, 0xD4, 0x34, 0xB4, 0x74, 0xF4,
0x0C, 0x8C, 0x4C, 0xCC, 0x2C, 0xAC, 0x6C, 0xEC,
0x1C, 0x9C, 0x5C, 0xDC, 0x3C, 0xBC, 0x7C, 0xFC,
0x02, 0x82, 0x42, 0xC2, 0x22, 0xA2, 0x62, 0xE2,
0x12, 0x92, 0x52, 0xD2, 0x32, 0xB2, 0x72, 0xF2,
0x0A, 0x8A, 0x4A, 0xCA, 0x2A, 0xAA, 0x6A, 0xEA,
0x1A, 0x9A, 0x5A, 0xDA, 0x3A, 0xBA, 0x7A, 0xFA,
0x06, 0x86, 0x46, 0xC6, 0x26, 0xA6, 0x66, 0xE6,
0x16, 0x96, 0x56, 0xD6, 0x36, 0xB6, 0x76, 0xF6,
0x0E, 0x8E, 0x4E, 0xCE, 0x2E, 0xAE, 0x6E, 0xEE,
0x1E, 0x9E, 0x5E, 0xDE, 0x3E, 0xBE, 0x7E, 0xFE,
0x01, 0x81, 0x41, 0xC1, 0x21, 0xA1, 0x61, 0xE1,
0x11, 0x91, 0x51, 0xD1, 0x31, 0xB1, 0x71, 0xF1,
0x09, 0x89, 0x49, 0xC9, 0x29, 0xA9, 0x69, 0xE9,
0x19, 0x99, 0x59, 0xD9, 0x39, 0xB9, 0x79, 0xF9,
0x05, 0x85, 0x45, 0xC5, 0x25, 0xA5, 0x65, 0xE5,
0x15, 0x95, 0x55, 0xD5, 0x35, 0xB5, 0x75, 0xF5,
0x0D, 0x8D, 0x4D, 0xCD, 0x2D, 0xAD, 0x6D, 0xED,
0x1D, 0x9D, 0x5D, 0xDD, 0x3D, 0xBD, 0x7D, 0xFD,
0x03, 0x83, 0x43, 0xC3, 0x23, 0xA3, 0x63, 0xE3,
0x13, 0x93, 0x53, 0xD3, 0x33, 0xB3, 0x73, 0xF3,
0x0B, 0x8B, 0x4B, 0xCB, 0x2B, 0xAB, 0x6B, 0xEB,
0x1B, 0x9B, 0x5B, 0xDB, 0x3B, 0xBB, 0x7B, 0xFB,
0x07, 0x87, 0x47, 0xC7, 0x27, 0xA7, 0x67, 0xE7,
0x17, 0x97, 0x57, 0xD7, 0x37, 0xB7, 0x77, 0xF7,
0x0F, 0x8F, 0x4F, 0xCF, 0x2F, 0xAF, 0x6F, 0xEF,
0x1F, 0x9F, 0x5F, 0xDF, 0x3F, 0xBF, 0x7F, 0xFF,
};
unsigned int I, J;
unsigned char *Ic = (unsigned char*) &I;
unsigned char *Jc = (unsigned char*) &J;
for(I = 1; I < N - 1; I++)
{
Jc[0] = reverse256[Ic[3]];
Jc[1] = reverse256[Ic[2]];
Jc[2] = reverse256[Ic[1]];
Jc[3] = reverse256[Ic[0]];
J >>= (32 - T);
if (I < J)
{
S = x[I];
x[I] = x[J];
x[J] = S;
}
}
Напомним основные формулы:
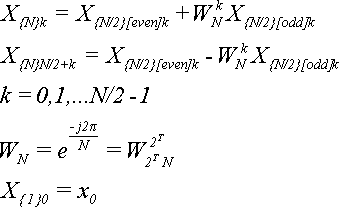(16)
На рисунке проиллюстрирован второй этап вычисления ДПФ. Линиями сверху вниз показано использование элементов для вычисления значений новых элментов. Очень удобно то, что два элемента на определенных позициях в массиве дают два элемента на тех же местах. Только принадлежать они будут уже другим, более длинным массивам, размещенным на месте прежних, более коротких. Это позволяет обойтись одним массивом данных для исходных данных, результата и хранения промежуточных результатов для всех T итераций.
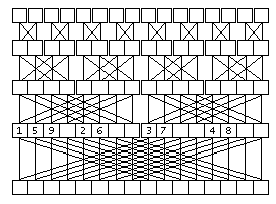
рис. 4
Итак, вот действия, которые нужно выполнить после первичной перестановки элементов.
#define T 4
#define Nmax (2 << T)
complex Q, Temp, j(0,1);
static complex x[Nmax];
static double pi2 = 2 * 3.1415926535897932384626433832795;
int N, Nd2, k, mpNd2, m;
for(N = 2, Nd2 = 1; N <= Nmax; Nd2 = N, N += N)
{
for(k = 0; k < Nd2; k++)
{
W = exp(-j*pi2*k/N);
for(m = k; m < Nmax; m += N)
{
mpNd2 = m + Nd2;
Temp = W * x[mpNd2];
x[mpNd2] = x[m] - Temp;
x[m] = x[m] + Temp;
}
}
}
Переменная Nmax содержит полную длину массива данных и окончательное количество элементов ДПФ. В таблице показано соответствие между выражениями в формуле (16) и переменными в программе.
|
В алгоритме |
В формуле |
|
N |
N |
|
Nd2 |
N/2 |
|
k |
k |
|
m |
k с поправкой на номер последовательности |
|
mpNd2 |
k+N/2 с поправкой на номер последовательности |
|
pi2 |
2π |
|
j |
j (мнимая единица) |
|
x[k] (в начале цикла) |
X{N/2}[even]k |
|
x[mpNd2] (в начале цикла) |
X{N/2}[odd]k |
|
x[k] (в конце цикла) |
X{N}k |
|
x[mpNd2] (в конце цикла) |
X{N}N/2+k |
|
W |
|
Внешний цикл - это основные итерации. На каждой из них 2Nmax/N ДПФ (длиной по N/2 элементов каждое) преобразуются в Nmax/N ДПФ (длиной по N элементов каждое).
Следующий цикл по k представляет собой цикл синхронного вычисления элементов с индексами k и k + N/2 во всех результирующих ДПФ.
Самый внутренний цикл перебирает Nmax/N штук ДПФ одно за другим.
Именно так, а не иначе: сначала вычисляются элементы с номерами 0 и N/2, во всех ДПФ в количестве Nmax/N штук, потом с номерами 1 и N/2 + 1 и так далее. На рис.4 показана последовательность вычислений для N = 8. Такая последовательность обеспечивает однократное вычисление 
.
Обратите внимание, что x[mpNd2] вычисляется раньше, чем x[k], чтобы значение x[k] не было модифицировано прежде, чем будет использовано.
Алгоритм обратного дискретного преобразования Фурье отличается только тем, что вместо -j надо использовать +j и после всех вычислений поделить каждое x[k] на Nmax.
Для справки: произведение, сумма и экспонента для комплексных чисел вычисляются по формулам:
(x,y)(x',y')=(xx'-yy')(xy'+x'y)
(x,y)+(x',y')=(x+x')(y+y')
e-jv=(cos v, - sinv)
где v - действительное число.
В приведенной выше программе велико искушение для вычисления поворачивающих множителей использовать формулу:
. (17)
Это позволило бы избавиться от возведений в степень и обойтись одними умножениями, если заранее вычислить WN для N = 2, 4, 8,…, Nmax. Но то, что можно делать в математике, далеко не всегда можно делать в программах. По мере увеличения k поворачивающий множитель будет изменяться, но вместе с тем будет расти погрешность. Ведь вычисления с плавающей точкой на реальном компьютере совсем без погрешностей невозможны. И после N/2 подряд умножений в поворачивающем множителе может накопиться огромное отклонение от точного значения. Вспомним правило: при умножении величин их относительные погрешности складываются. Так что, если погрешность одного умношения равна s%, то после 1000 умножений она может достигнуть в худшем случае 1000s%.
Этого можно было бы избежать, будь число WN целым, но оно не целое при N > 2, так как вычисляется через синус и косинус:
Как же избежать множества обращений к весьма медленным функциям синуса и косинуса? Здесь нам приходит на помощь давно известный алгоритм вычисления степени через многократные возведения в квадрат и умножения. Например:
В данном случае нам понадобилось всего 5 умножений (учитывая, что 
не нужно вычислять дважды) вместо 13. В худшем случае для возведения в степень от 1 до N/2-1 нужно log2N умножений вместо N/2, что дает вполне приемлемую погрешность для большинства практических задач.
Можно сократить вдвое количество умножений на каждом шаге, если использовать результаты прошлых вычислений
,
для хранения которых нужно дополнительно log2(Nmax) комплексных ячеек памяти:
Если очередное не было вычислено предварительно, то берется двоичное представление k и анализируется. Каждому единичному биту соответствует ровно один множитель. В общем случае единице в бите с номером b (младший бит имеет номер 0) соответствует множитель 
, который хранится в b-й ячейке упомянутого выше массива.
Есть способ уменьшить количество умножений для вычисления до одного на два цикла. Но для этого нужно отвести N/2 комплексных ячеек для хранения всех предыдущих . Алгоритм достаточно прост. Нечетные элементы вычисляются по формуле (17). Четные вычисляются по формуле:
То есть, ничего не вычисляется, а берется одно из значений, вычисленных на предыдущем шаге, когда N было вдвое меньше. Чтобы не нужно было копировать величины на новые позиции достаточно их сразу располагать в той позиции, которую они займут при N = Nmax и вводить простую поправку Skew (см. листинг программы).
И последние пояснения относительно листинга.
Во-первых, здесь присутствует реализация простейших операций над комплексными числами (классы Complex и ShortComplex), оптимизированная под данную задачу. Обычно та или иная реализация уже есть для многих компиляторов, так что можно использовать и ее.
Во-вторых, массив W2n содержит заранее вычисленные коэффициенты W2, W4, W8,...,WNmax.
В-третьих, для вычислений используются наиболее точное представление чисел с плавающей точкой в C++: long double размером в 10 байт на платформе Intel. Для хранения результатов в массивах используется тип double длиной 8 байт. Причина - не в желании сэкономить 20% памяти, а в том, что 64-битные и 32-битные процессоры лучше работают с выровненными по границе 8 байт данными, чем с выровненными по границе 10 байт.
Для чего нужно быстрое преобразование Фурье или вообще дискретное преобразование Фурье (ДПФ)? Давайте попробуем разобраться.
Пусть у нас есть функция синуса x = sin(t).
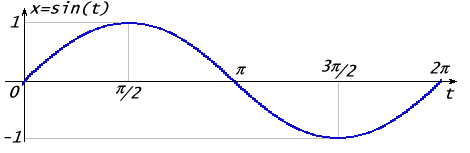
Максимальная амплитуда этого колебания равна 1. Если умножить его на некоторый коэффициент A, то получим тот же график, растянутый по вертикали в A раз: x = Asin(t).
Период колебания равен 2π. Если мы хотим увеличить период до T, то надо умножить переменную t на коэффициент. Это вызовет растяжение графика по горизонтали: x = A sin(2πt/T).
Частота колебания обратна периоду: ν = 1/T. Также говорят о круговой частоте, которая вычисляется по формуле: ω= 2πν = 2πT. Откуда: x = A sin(ωt).
И, наконец, есть фаза, обозначаемая как φ. Она определяет сдвиг графика колебания влево. В результате сочетания всех этих параметров получается гармоническое колебание или просто гармоника:
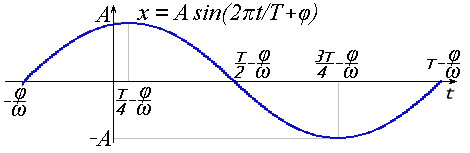
Очень похоже выглядит и выражение гармоники через косинус:
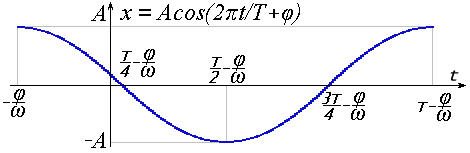
Большой разницы нет. Достаточно изменить фазу на π/2, чтобы перейти от синуса к косинусу и обратно. Далее будем подразумевать под гармоникой функцию косинуса:
x = A cos(2πt/T + φ) = A cos(2πνt + φ) = A cos(ωt + φ) (18)
В природе и технике колебания, описываемые подобной функцией чрезвычайно распространены. Например, маятник, струна, водные и звуковые волны и прочее, и прочее.
Преобразуем (18) по формуле косинуса суммы:
x = A cos φ cos(2πt/T) - A sin φ sin(2πt/T) (19)
Выделим в (19) элементы, независимые от t, и обозначим их как Re и Im:
x = Re cos(2πt/T) - Im sin(2πt / T) (20)
Re = A cos φ, Im = A sin φ
По величинам Re и Im можно однозначно восстановить амплитуду и фазу исходной гармоники:
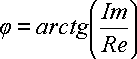и 
(21)
Рассмотрим очень распространенную практическую ситуацию. Пусть у нас есть звуковое или какое-то иное колебание в виде функции x = f(t). Пусть это колебание было записано в виде графика для отрезка времени [0, T]. Для обработки компьютером нужно выполнить дискретизацию. Отрезок делится на N-1 равных частей, границы частей обозначим tn = nT/N. Сохраняются N значений функции на границах частей: xn = f(tn) = { x0, x1, x2,..., xN }.
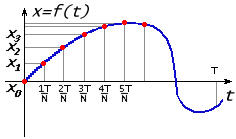
В результате прямого дискретного преобразования Фурье были получены N значений для Xk:
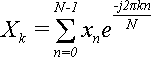(22)
Теперь возьмем обратное преобразование Фурье:
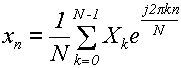(23)
Выполним над этой формулой следующие действия: разложим каждое комплексное Xk на мнимую и действительную составляющие Xk = Rek + j Imk; разложим экспоненту по формуле Эйлера на синус и косинус действительного аргумента; перемножим; внесем 1/N под знак суммы и перегруппируем элементы в две суммы:
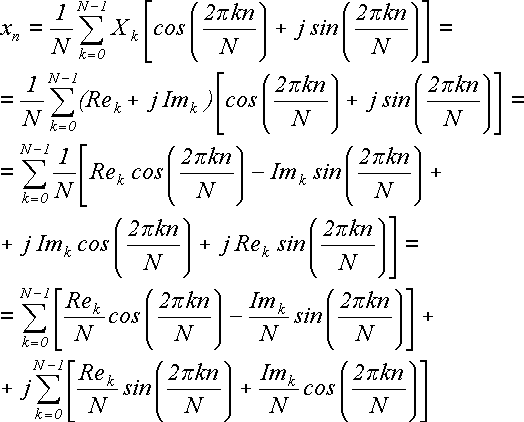(24)
Это была цепочка равенств, которая начиналась с действительного числа xn. В конце получилось две суммы, одна из которых помножена на мнимую единицу j. Сами же суммы состоят из действительных слагаемых. Отсюда следует, что вторая сумма должна быть равна нулю. Отбросим ее и получим:
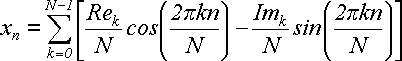(25)
Поскольку при дискретизации мы брали tn = nT/N и , то можем выполнить замену: n = tnN/T. Следовательно, в синусе и косинусе вместо 2πkn/N можно написать 2πktn/T. В результате получим:
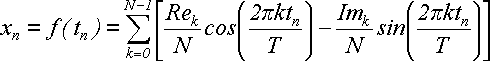(26)
Сопоставим эту формулу с формулой (20) для гармоники:
x = Re cos(2πt/T) - Im sin(2πt / T) (20)
Слагаемые суммы (26) аналогичны формуле (20), а формула (20) описывает гармоническое колебание. Значит сумма (26) представляет собой сумму из N гармонических колебаний разной частоты, фазы и амплитуды.
Выше объяснялось, каким образом формула вида (20) может быть преобразована в формулу вида (18):
x = A cos(2πt/T + φ) (18)
Выполним такое же преобразование для слагаемых суммы (26), преобразуем их из вида (20) в вид (18). Получим:
(27)
Далее будем функцию
Gk(t) = Ak cos(2πtk/T + φk) (28)
называть k-й гармоникой.
Для вычисления Ak и φk надо использовать формулу (21). Теперь выпишем в одном месте все формулы, которые связывают амплитуду, фазу, частоту и период каждой из гармоник с коэффициентами Xk:
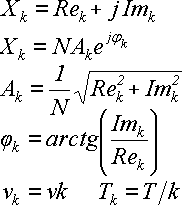(29)
Итак.
Физический смысл дискретного преобразования Фурье состоит в том, чтобы представить некоторый дискретный сигнал в виде суммы гармоник. Параметры каждой гармоники вычисляются прямым преобразованием, а сумма гармоник - обратным.
|
|
 |
