В этой главе на самых простых примерах мы разберем азы построений объектов.
Пока рассмотрим рисование только на плоскости, однако полученные знания постоянно
будут использоваться при переходе к рисованию в пространстве.
OpenGL является низкоуровневой библиотекой В частности это означает, что рисование
объемных фигур сводится к последовательному рисованию в пространстве плоских
фигур, образующих нужную объемную. Поэтому, даже если вас интересует только
использование 3D возможностей библиотеки, пропускать эту главу не рекомендуется.
Примеры располагаются на дискете в каталоге Chapter2.
Точка
Для начала скажем, что в OpenGL левый нижний угол области вывода имеет координаты
[-1; -1], правый верхний - [1, 1]
Начнем наше знакомство с примитивами OpenGL c самого простого из них - точки.
Нарисуем на экране пять точек, четыре по углам окна и одну в центре (проект
располагается в подкаталоге Ex01).
Обработчик события onPaxnt формы дополнился следующими строками
glViewPort (0, 0, ClientWidth, ClientHeight); // область вывода
glPointSize (20); // размер точек
glColor3f (1. 0, 1. 0, 1. 0); // цвет примитивов
glBegin (GL_POINTS); // открываем командную скобку
glVertex2f (-1, -1); // левый нижний угол
glVertex2f (-1, 1); // левый верхний угол
glVertex2f (0, 0);
glVertex2f (1, -1);
glVertex2f (l, 1); glEnd; SwapBuffers(Canvas. Handle)
// центр окна
// правый верхний угол
// правый нижний угол
// закрываем командную скобку
// содержимое буфера - на экран
Разберем каждую из строк программы подробно.
Первая строка задает область вывода указанием координат левого нижнего и правого
верхнего углов (в пикселах, в оконных координатах). Я взял в качестве области
вывода всю клиентскую часть окна. Если третий параметр процедуры glViewPort
записать как round (clientwidth / 2), то картинка вдвое сузится, но окрашено
будет все окно (проект из подкаталога Ex02).
Следующие две строки программы определяют параметры выводимых точек, размер
и цвет.
На примере команды glcolor3f разберем синтаксис команд OpenGL.
Из справки по этой команде вы узнаете, что она принадлежит к целому набору команд
glcolor с различными окончаниями: зb, 4i и прочие. Цифра в окончании соответствует
количеству требуемых аргументов, а следующая цифрой буква показывает требуемый
тип аргументов. To есть glColor3f требует в качестве аргументов тройку вещественных
(float) чисел, а glColor3i - тройку целых (int) чисел.
Аналогичный синтаксис мы встретим у многих других команд OpenGL
Здесь же, в справке, выясняем, что при записи функции в вещественной форме аргументы
лежат в интервале [0; 1], а в целочисленной форме - линейно отображаются на
этот интервал, т. e. для задания белого цвета целочисленная форма команды будет
выглядеть так:
glColor3i (2147483647, 2147483647, 2147483647); //цвет примитивов
где максимальное 8-битное целое без знака соответствует предельному значению
интервала.
Почти всегда предпочтительно использовать команду в вещественной форме, поскольку
OpenGL хранит данные именно в вещественном формате Исключения оговариваются
в файле справки.
Замечание
Если имя команды заканчивается на v (векторная форма), то аргументом ее служит
указатель на структуру, содержащую данные, например, массив To есть, например,
если последние три символа в имени команды 3fv, то ее аргумент - адрес массива
трех вещественных чисел Использование такой формы команды является самым оптимальным
по скоростным характеристикам.
Далее в программе следуют функции (командные скобки) glBegin и glEnd, между
которыми заключены собственно процедуры рисования. Разберемся подробнее с функциями
giBegm и glEnd ввиду их особой важности: большинство графических построений
связано с использованием именно этой пары функций.
Во-первых, необходимо уяснить, что это командные скобки библиотеки OpenGL, не
заменяющие операторные скобки языка Pascal и не имеющие к ним никакого отношения
Ошибка при использовании командных скобок не распознается компилятором. Если
в программе написана неправильная вложенность командных скобок OpenGL, то ошибка
проявится только в процессе диалога приложения с сервером.
Во-вторых, внутри этих скобок могут находиться любые операторы языка Pascal
и почти любые функции OpenGL (вернее, очень многие) Включенные в скобки команды
OpenGL отрабатываются так же, как и за пределами этих скобок Главное назначение
командных скобок - это задание режима (примитива) для команд givertex (вершина),
определяющих координаты вершин для рисования примитивов OpenGL.
В рассмотренном примере аргументом функции giBegin я взял символическую константу
GL^POINTS Из файла справки выясняем, что в этом случае все встретившиеся до
закрывающей скобки glEnd вершины (аргументы givertex) задают координаты очередной
отдельной точки. Команду givertex я взял в форме с двумя вещественными аргументами.
Получив справку по givertex, вы можете убедиться, что и эта команда имеет целый
ворох разновидностей.
Мы собирались нарисовать четыре точки по углам окна и одну в центре, поэтому
между командными скобками располагаются пять строк с вызовом givertex, аргументы
которых соответствуют положениям точек в системе координат области вывода библиотеки
OpenGL.
Сейчас обратите внимание на то, что вместе с изменением размеров окна рисуемое
изображение также изменяется: точки всегда рисуются на своих местах относительно
границ окна. Следующее замечание тоже очень важно обработчик события onResize
формы тот же, что и у события OnPaint.
Приведу еще несколько простых примеров на рисование точек
Если надо нарисовать десять точек по диагонали, то можно написать так (пример
располагается в подкаталоге Ех0З):
giBegin (GL_POINTS);
For i := 0 to 9 do
glVertex2f (i / 5 - 1, i / 5 - 1);
glEnd;
Ну а следующий код нарисует сотню точек со случайными координатами и цветами
(пример из подкаталога Ех04):
giBegin (GL_POINTS);
For i := 1 to 100 do begin
glColor3f (random, random, random); glVertex2f (random * 2 - 1, random * 2-1);
end;
glEnd;
Из этого примера мы видим, что команда, задающая цвет примитивов, может присутствовать внутри командных скобок OpenGL. Вызов же команды gipomtsize между командными скобками безрезультатен и будет генерировать внутреннюю ошибку OpenGL. Так что если мы хотим получать точки случайных размеров, цикл надо переписать так (проект из подкаталога Ех05):
For i := I to 100 do begin
glColorSf (random, random, random);
glPointSize (random (20)); // обязательно за пределами скобок
giBegin (GL_POINTS);
glVertex2f (random * 2 - 1, random * 2 - 1);
glEnd;
end;
Скорее всего, вас удивило то, что точки рисуются в виде квадратиков Чтобы получить точки в виде кружочков, перед giBegin вставьте строку
glEnable (GL_POINT_SMOOTH); // включаем режим сглаживания точек
Пара команд glEnable и giDisabie играет в OpenGL очень важную роль, включая
и отключая режимы работы следующих за ними команд. Нам придется еще не раз обращаться
к возможным аргументам этих функций, задающим, какой конкретно режим включается
или отключается.
Заканчивается обработчик события OnPaint вызовом SwapBuffers. Эта команда используется
в режиме двойной буферизации для вывода на экран содержимого заднего буфера.
Замечание
Вспомним в режиме двойной буферизации все рисование осуществляется в задний
буфер кадра, он является текущим на всем процессе воспроизведения По команде
SwapBuffers текущее содержимое переднего буфера подменяется содержимым заднего
буфера кадра, но текущим буфером после этого все равно остается задний.
Команда giciear с аргументом GL_COLOR_BUFFER_BIT очищает текущий буфер вывода.
Иногда в некоторых программах вы можете встретить, что серия команд рисования очередного кадра заканчивается командой giFimsh, ожидающей, пока все предыдущие команды OpenGL выполнятся, или же командой glFiush, ускоряющей выполнение предыдущих команд.
Замечание
В большинстве примеров этих лекций не используетя вызов glFinish или glFlush,
ускорение от них получается микроскопическим. Но в программах, не применяющих
двойную буферизацию, эти команды должны вызываться обязательно, иначе на экране
может оказаться "недорисованная" картинка.
Надеюсь, теперь каждая строка рассмотренной программы вам ясна Приведу еще одну иллюстрацию - занятный пример на использование полученных знаний. В разделе private опишите две переменные:
xpos: GLfloat; // координаты курсора в системе координат
OpenGL ypos: GLfloat;
Создайте следующий обработчик события MouseMove формы
xpos: = 2 * X / ClientWidth - 1;
ypos: = 2 * (ClientHeight - Y) / ClientHeight - 1;
Refresh; // перерисовываем окно
В обработчике события Paint опишите локальную целочисленную переменную i и содержательную часть кода приведите к виду
For i: = 1 to 40 do begin // сорок точек
glColor3f (random, random, random); // случайного цвета
glPointSize (random (10)); // случайного размера
glBegin (GL_POINTS}; // со случайными координатами вокруг курсора
glVertex2f (xpos + 0. 2 * random * sin (random (360)),
ypos + 0. 2 * random * cos (random (3 60)));
glEnd;
end;
Если все сделано правильно, при движении курсора по поверхности формы в районе
курсора появляется облачко разноцветных точек (готовый проект я поместил в подкаталог
Ex06). Разберитесь в этом примере с масштабированием значения переменных xpos
и ypos и обратите внимание, что обработчик движения мыши заканчивается вызовом
Refresh - принудительной перерисовкой окна при каждом движении курсора.
Предлагаю также разобрать простой пример из подкаталога Ex07 - построение синусоиды
средствами OpenGL:
procedure TfrmGL. FormPaint(Sender: TObject);
const
а = -Pi; // начало интервала
b = Pi; // конец интервала
num = 200; // количество точек на интервале
var
x: GLfloat;
l: GLint; begin wglMakeCurrent(Canvas. Handle, hrc);
glViewPort (0, 0, ClientWidth, ClientHeight);
glClearColor (0. 5, 0. 5, 0. 75, 1. 0);
glClear (GL_COLOR_BUFFER_BIT);
glEnable (GL_POINT_SMOOTH);
glColor3f (1. 0, 0. 0, 0. 5);
glBegin (GL_POINTS); For i: = 0 to num do begin x: = а + i * (b - а) / num;
glVertex2f (2 * (x - а) / (b - а) - 1. 0, sin(x) * 0. 75);
end;
glEnd;
SwapBuffers(Canvas. Handle);
wglMakeCurrent(0, 0);
end;
Пример из подкаталога Ex08 демонстрирует вывод средствами OpenGL прямо на поверхность рабочего стола. Напоминаю, окно с нулевым значением дескриптора соответствует поверхности рабочего стола, чем мы и пользуемся в этом примере для получения ссылки на контекст устройства:
dc: = GetDC (0);
Для завершения работы приложения нажмите клавиши <Alt>+<F4> или <Esc>. Обратите внимание, что по завершении работы приложения перерисовываем рабочий стол:
InvalidateRect (0, nil, False);
Перерисовка здесь необходима для восстановления нормального вида рабочего стола.
Замечание
Подобный прием для создания полноэкранного приложения прекрасно работает на
компьютерах без акселератора, чего не скажу о компьютерах, оснащенных ускорителем.
В заключение разговора о точках приведу одно маленькое, но важное замечание:
помимо константы GL_poiNTS в OpenGL имеется символическая константа GL_poiNT,
использующаяся в других, нежели glBegin, командах Но компилятор Delphi, конечно,
не сможет распознать ошибку, если вместо одной константы OpenGL указать другую,
когда типы констант совпадают. В этом случае ошибка приведет только к тому,
что не будет построено ожидаемое изображение, аварийное завершение работы приложения
не произойдет.
To же самое справедливо для всех рассматриваемых далее констант - необходимо
внимательно следить за синтаксисом используемых команд.
Команда glScissor
Вернемся к проекту из подкаталога Ex02, в котором область вывода задается на
половину экрана. Возможно, вас этот пример не удовлетворил: хотя картинка и
выводится на половину экрана, окрашивается все-таки весь экран, а иногда это
нежелательно и необходимо осуществлять вывод именно в пределах некоторой части
окна.
Решение может заключаться в использовании функции вырезки glscissor, определяющей
прямоугольник в окне приложения, т. e. область вырезания. После того как область
вырезки задана, дальнейшие команды воспроизведения могут модифицировать только
пикселы, лежащие внутри области (формулировка взята из файла справки).
Для использования этой функции необходимо включить режим учета вырезки:
glEnable(GL_SCISSOR_TEST);
После использования вырезки этот режим необходимо отключить парной командой
glDisable.
Разберите проект из подкаталога Ex09 (второй пример этой главы), дополненный
строками включения режима вырезки и командой, задающей область вырезки:
glEnable(GL_SCISSOR_TEST}; // включаем режим использования вырезки.
glScissor(0, 0, round(ClientWidth/2), ClientHeight); // область вырезки
Функция glScissor не заменяет команды glviewport, задающей область вывода: если в этом примере область вывода распространить на весь экран, то на экране будет рисоваться половина картинки, т. e. только то, что попадает в область вырезки.
Совместный вывод посредствомфункций GDi и
OpenGL
Возможно, вы заинтересовались вопросом, можно ли перемежать функции вывода GDI
и OpenGL. Вопрос этот, конечно, носит скорее академический, чем практический
характер.
Совместное использование поверхности окна возможно при условии, что канва будет
доступна для вывода, т. e. в этом случае надо обязательно освобождать контексты.
Замечание:
Многое также зависит от графической карты компьютера.
Посмотрите несложный пример из подкаталога Ex10, где код перерисовки окна первого
примера данной главы дополнен строками:
Canvas. Brush. Color: = clGreen;
Canvas. Ellipse (10, 10, 50, 50);
Обратите внимание, что эти строки располагаются после строки, освобождающей контекст воспроизведения. Если поставить вывод средствами GDI перед этой строкой, вывода не произойдет, а если поставить до строки, устанавливающей контекст воспроизведения, то картинка, выдаваемая OpenGL, закроет нарисованное изображение.
Отрезок
От точек перейдем к линиям. Разберем следующий возможный аргумент команды glBegm
- константу GL_LiNES, задающий примитив "независимый отрезок".
Для этого примитива следующие в командных скобках вершины (т. e. функции glvertex)
задают попарно координаты начала и конца каждого отрезка прямой. Снова вернемся
к первому примеру с точками и подправим код рисования следующим образом (готовый
проект можете найти в подкаталоге Ex11):
glBegin (GL_LINES);
glVertex2f (-1, 1);
glVertex2f (1, -1);
glVertex2f (-1, -1);
glVertex2f (1, 1);
glEnd;
Рисуются два отрезка, соединяющие углы окна по диагоналям.
Для увеличения толщины отрезков перед командными скобками укажите ширину линии:
glLineWidth (2. 5);
Эта функция также должна выноситься за командные скобки
Как и у точек, у линий можно устранять ступенчатость. Исправьте код следующим
образом (подкаталог Ex12):
glLineWidth (15);
glEnable (GL_LINE_SMOOTH);
glBegin (GL_LINES);
glVertex2f (-0. 7, 0. 7);
вызовом и без вызова и посмотрите результаты работы программы с
glEnable (GL_LINE_SMOOTH).
Итак, константа GL_LiNES задает примитив отдельных отрезков, определенных указанием
пар вершин. Понятно, что количество вершин должно быть четным.
Следующая константа - GL_LiNE_STRip - определяет примитив, когда перечисляемые
вершины последовательно соединяются одна за другой. Приводимый код поясняет
отличие этого примитива от предыдущего.
glBegin (GL_LINE_STRIP);
glVertex2f (-l, -1);
glVertex2f (-1, 1);
glVertex2f (1, 1);
glVertex2f (l, -l);
glEnd;
Результат - буква П по границе окна (проект из подкаталога Exl3) В примитиве, задаваемом константой GL_LiNE_Loop, также последовательно соединяются перечисляемые вершины, однако последняя вершина замыкается с самой первой. Если в предыдущем примере использовать GL_LiNE__ Loop, будет построен квадрат по границе окна (подкаталог Exl4). В примерах на отрезки мы пока использовали непрерывную линию. Для рисования пунктирной линией перед командными скобками добавьте следующие строки (проект из подкаталога Exl5):
glLineStipple (1, $FOFO);
glEnable (GL_LINE_STIPPLE);
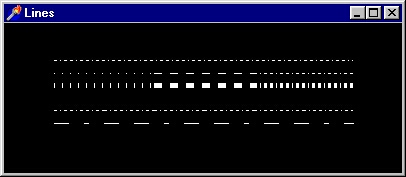
У функции glLinestipple первый аргумент - масштабный множитель, второй аргумент задает шаблон штриховки (побитовым способом). Разберем проект из подкаталога Exl6 - еще один пример на использование штриховки (рис. 2. 1).

Рис. 2. 1. Несколько готовых шаблонов штриховых линий
Пользовательская процедура drawOneLine вызывается для воспроизведения каждого
отдельного отрезка:
procedure TfrmGL. drawOneLine(xl, yl, x2, y2: GLfloat);
begin glBegin(GL_LINES);
glVertex2f glVertex2f glEnd;
end;
(2 * xl / ClientWidth - 1. 0, yl (2 * x2 / ClientWidth - 1. 0, y2
/ ClientHeight - 0. 5); / ClientHeight - 0. 5);
Содержательная часть кода перерисовки окна выглядит так:
glColor3f (1. 0, 1. 0, 1. 0); // все отрезки рисуются белым
// вторая строка: рисуется 3 отрезка, все с различной штриховкой
glEnable (GL_LINE_STIPPLE);
glLineStipple (1, $0101); // точечный
drawOneLine (50. 0, 125. 0, 150. 0, 125. 0);
glLineStipple (1, $OOFF); // штрихи
drawOneLine (150. 0, 125. 0, 250. 0, 125. 0);
glLineStipple (1, $1C47); // штрихпунктир
drawOneLine (250. 0, 125. 0, 350. 0, 125. 0);
// третья строка: рисуется три широких отрезка с той же штриховкой
glLineWidth (5. 0); // задаем ширину линии
glLineStipple (1, $0101);
drawOneLine (50. 0, 100. 0, 150. 0, 100. 0);
glLineStipple (1, $00FF);
drawOneLine (150. 0, 100. 0, 250. 0, 100. 0);
glLineStipple (1, $1C47);
drawOneLine (250. 0, 100. 0, 350. 0, 100. 0);
glLineWidth (1. 0);
// в первой строке рисуется 6 отрезков, шаблон "пунктир/точка/пунктир",
// как части одного длинного отрезка, без вызова процедуры
drawOneLine glLineStipple (1, $1C47);
glBegin (GL_LINE_STRIP);
for i: = 0 to 6 do
glVertex2f ( 2 * (50. 0 + (i * 50. 0)) / ClientWidth - 1. 0, 75. 0 / ClientHeight);
glEnd;
// Четвертая строка - аналогичный результат, но 6 отдельньк отрезков
for i: = 0 to 5 do
drawOneLine (50. 0 + i * 50. 0, 50. 0, 50. 0 + (i+l) * 50. 0, 50. 0); // пятая
строка - рисуется один штрихпунктирный отрезок, множитель = 5 glLineStipple
(5, $1С47);
drawOneLine (50.0, 25.0, 350.0, 25.0);
В заключение разговора по поводу линий посмотрите проект из подкаталоге Ех17 - модифицированный пример с отслеживанием позиции курсора Теперь картинка напоминает бенгальский огонь - рисуются отрезки случай ного цвета, длины, штриховки:
glEnable (GL_LINE_STIPPLE) ;
For i := 1 to 100 do begin ,
glColor3f (random, random, random);
glLineStipple (random (5), random ($FFFF) ) ;
glBegin (GL_LINES);
glVertex2f (xpos, ypos) ;
glVertex2f (xpos + 0.5 * random * sin (random (360)),
ypos + 0.5 * random * cos (random (360)));
glEnd;
end;
Треугольник
Закончив с линиями, перейдем к треугольникам - примитиву, задаваемому константой
GLJTRIANGLES. В этом примитиве последующие вершины берутся триплетами, тройками,
по которым строится каждый отдельный треугольник.
Следующий код служит иллюстрацией рисования одного треугольника (проект из подкаталога
Ех18).
glBegm (GLJTRIANGLES) ;
glVertex2f (-1, -1);
glVertex2f (-1, 1);
glVertex2f (1, 0);
glEnd;
Для рисования правильного шестиугольника из отдельных треугольников код должен выглядеть так (готовую программу можете найти в подкаталоге Ех19):
glBegm (GLJTRIANGLES) ;
For i := 0 to 5 do begin glVertex2f (0, 0);
glVertex2f (0.5 * cos (2 * Pi * i / 6), 0.5 * sin (2 * Pi * i / 6));
glVertex2f (0.5 * cos (2 * Pi * (i + 1) /6),
0.5 * sin (2 * Pi * (i + 1) / 6) ) ;
end;
glEnd;
В качестве опорных точек выбраны шесть точек на окружности.
Надеюсь, здесь не требуется дополнительных пояснений, и мы можем перейти к примитиву,
задаваемому константой GL_TRIANGLE_STRIP' связанная группа треугольников. Первые
три вершины образуют первый треугольник, вершины со второй по четвертую - второй
треугольник, с третьей по пятую - третий и т. д.
Проект из подкаталога Ех20 нарисует флажок, образованный наложением двух треугольников
(рис. 2.2):

Рис. 2.2. Флаг получается наложением Двух отдельных треугольников
glBegm (GL_TRIANGLE_STRIP) ;
glVertex2f (1,1);
glVertex2f (-1, I);
glVertex2f (-1, -1);
glVertex2f (1, -1);
glEnd;

Рис. 2.3. Эту картинку попробуйте нарисовать самостоятельно
А сейчас для тренировки попробуйте изменить код так, чтобы была нарисована
такая же картинка, как на рис. 2.3.
Попробуем поэкспериментировать с нашей программой: будем рисовать треугольники
разного цвета (проект из подкаталога Ех21):
glBegm (GL_TRIANGLE_STRIP) ;
glColorSf (0.0, 0.0, 1.0);
glVertex2f (1, 1);
glVertex2f (-1, 1);
glColor3f (1. 0, 0. 0, 0. 0);
glVertex2f (-l, -1);
glVertex2f (1, -1);
glEnd;
Результат окажется неожиданным и живописным: у фигуры возникнет плавный переход синего цвета в красный (рис. 2. 4).
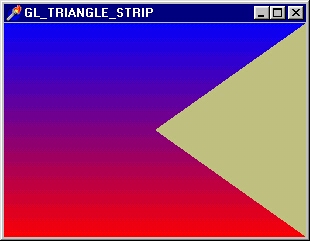
Рис. 2. 4. Плавный переход цвета
Вызов перед командными скобками функции glshadeModel(GL_FLAT), задающей правило
тонирования, избавит от градиентного заполнения фигуры, но результат все равно
будет неожиданным - оба треугольника станут красными, т. e. цвета второго из
них (проект находится в подкаталоге Ex22). Ознакомившись со справкой по этой
команде, мы обнаружим, что для связанных треугольников наложение цветов происходит
именно по правилу старшинства цвета второго примитива. Здесь же узнаем, что
по умолчанию тонирование задается плавным, как и получилось в предыдущей программе.
В продолжение экспериментов код рисования приведем к следующему виду:
glBegin (GL_TRIANGLE_STRIP);
glVertex2f (random * 2 - 1, random * 2 - 1);
For i: = 0 to 9 do begin
glColor3f (random, random, random);
glVertex2f (random * 2 - 1, random * 2 - 1);
glVertex2f (random * 2 - 1, random * 2 - 1);
end;
glEnd;
Результат получается также интересный: на экране рисуются калейдоскопические картинки, некоторые из них вполне могут порадовать глаз. Пример одной из таких картинок приведен на рис. 2. 5.

Рис. 2. 5. Результат работы программы из каталога Chapter2\Ex23
Предлагаю вам создать обработчик нажатия клавиши, включающий в себя вызов функции
Refresh, тогда по нажатию любой клавиши картинка будет меняться (в подкаталоге
Ex23 можете взять готовый проект).
Теперь добавьте в программу вызов glshadeModel с аргументом GL_FLAT и обратите
внимание, что треугольники окрашиваются попарно одинаковым цветом. Позже мы
поговорим о том, по какому правилу отображаемые примитивы накладываются друг
на друга, а пока просто понаблюдайте, как рисуется подобие смятой бумажной змейки
(треугольники последовательно накладываются друг на друга).
рисование шестиугольника путем наложения треугольников может быть реализовано
с помощью следующего кода (пример располагается в подкаталоге Ex24):
glBegin (GL_TRIANGLE_STRIP);
For i: = 0 to 6 do begin
glColor3f (random, random, random);
glVertex2f (0, 0);
glVertex2f (0. 5 * cos (2 * Pi * i / 6),
0. 5 * sin (2 * Pi * i / 6) );
end;
glEnd;
Обязательно посмотрите результат работы этой программы, а также потренируйтесь
в выборе различных моделей тонирования.
Проект из подкаталога Ex25 тоже советую не пропустить: здесь находится небольшая
модификация предыдущего примера. Увеличение количества опорных точек привело
к симпатичному результату: рисуется окружность с подобием интерференционной
картинки на поверхности компакт-диска. Картинка меняется при нажатии клавиши
и при изменении размеров окна. Следующий примитив, определяемый константой GL_TRiANGLE_FAN,
также задает последовательно связанные треугольники, однако фигура строится
по другому принципу: первая вершина является общей для всех остальных треугольников,
задаваемых перечислением вершин, т. e. треугольники связываются наподобие веера.
Для построения шестиугольника с использованием такого примитива цикл надо переписать
так (проект находится в подкаталоге Ex26):
glBegm (GL_TRIANGLE_FAN);
glVertex2f (0, 0); // вершина, общая для всех треугольников
For i: = о to 6 do begin
glColor3f (random, random, random);
glVertex2f (0. 5 * cos (2 * Pi * i / 6),
0. 5 * sin (2 * Pi * i / 6) );
end;
Теперь поговорим о режимах вывода многоугольников. Для устранения ступенчатости многоугольников используется команда:
glEnable с аргументом GL_POLYGON__SMOOTH.
Если в примеры на треугольники перед командными скобками поместить строку:
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
то треугольники будут рисоваться контурно - только линии границ (проект находится в подкаталоге Ex27).
Замечание
Запомните, что команда glPolygonMode задает режим воспроизведения для всех типов
многоугольников.
Ширину линий контура можно варьировать с помощью glLineWidth, пунктирные линии
контура задаются командой glLinestipple. Команда glPolygonMode позволяет выводить
вместо заполненных и контурных многоугольников только их вершины, если ее вторым
аргументом взять константу GL_POiNT (не путать с GL_PoiNTs!). Размеры точек
вершин и наличие сглаживания у них можно задавать так же, как и для обычных
точек. По умолчанию многоугольники строятся заполненными (включен режим GL_FILL).
Команда glPolygonMode заставляет обратить внимание на порядок перечисления вершин,
задающий лицевую и обратную сторону рисуемых фигур. Этот порядок для рассматриваемых
плоскостных построений задает пока только то, какую сторону рисуемой фигуры
мы видим, что в данном случае не особо существенно, но для будущего важно хорошо
разобраться в этом вопросе.
В программе из подкаталога Ex28 рисуется все тот же шестиугольник, но вершины
перечислены в обратном порядке. Контурный режим, включенный для лицевой стороны
вызовом:
glPolygonMode(GL_FRONT, GL_LINE);
не приводит ни к каким изменениям в рисунке, поскольку мы видим не лицевую,
а изнаночную сторону объекта, режим рисования которой мы не меняли, следовательно,
он остался принятым по умолчанию, т. e. сплошной заливкой.
Сейчас самое время поэкспериментировать с режимами воспроизведения многоугольников.
В последней программе задайте различные режимы и посмотрите, к каким изменениям
это приведет.
Мы изучили примитивы "точка", "линия", "треугольник".
В принципе, этих примитивов вполне достаточно, чтобы нарисовать все что угодно,
пусть подчас и чересчур громоздким способом. Даже более того, остальные примитивы
фактически являются усовершенствованными треугольниками и строятся из треугольников,
чем и вызваны их некоторые ограничения. Построения на основе треугольников являются
оптимальными по своим скоростным показателям: треугольники строятся наиболее
быстро, и именно этот формат чаще всего предлагается для аппаратного ускорения.
Замечание
По возможности старайтесь использовать связанные треугольники.
Но наш разговор о примитивах OpenGL был бы, конечно, не полным, если бы мы остановились
на данной этапе и оставили без рассмотрения оставшиеся примитивы-многоугольники.
Многоугольник
Для рисования прямоугольника на плоскости можно воспользоваться командой glRectf.
Это одна из версий команды glRect. Ее аргументом являются координаты двух точек
- противоположных углов рисуемого прямоугольника. Посмотрите проект, располагающийся
в подкаталоге Ex29 - простой пример на построение прямоугольника с использованием
этой команды.
Замечание
При использовании glRect необходимо помнить, что координата по оси Z в текущей
системе координат для всех вершин равна нулю.
Константа GL_QUADS задает примитив, когда перечисляемые вершины берутся по четыре
и по ним строятся независимые четырехугольники.
Следующий код - иллюстрация использования этого примитива: строятся два независимых
четырехугольника (взято из проекта, располагающегося в подкаталоге Ех30).
glBegin (GL_QUADS);
glColor3f (random, random, random);
glVertex2f (-0. 6, 0. 2);
glVertex2f (-0. 7, 0. 7);
glVertex2f (0. 1, 0. 65);
glVertex2f (0. 25, -0. 78);
glColor3f (random, random, random);
glVertex2f (0. 3, -0. 6);
glVertex2f (0. 45, 0. 7);
glVertex2f (0. 8, 0. 65);
glVertex2f (0. 9, -0. 8);
glEnd;
Результат работы программы иллюстрирует рис. 2. 6.
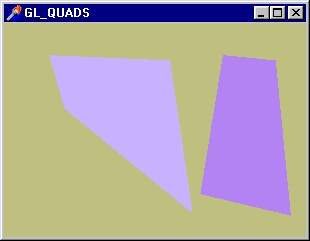
Рис. 2. 6. Для построения независимых четырехугольников используется
примитив, задаваемый константой
GL QUADS
Примитив, задаваемый константой GL_QUAD_STRip, состоит из связанных четырехугольников
Первый четырехугольник формируется из вершин номер один, два, три и четыре.
Второй четырехугольник в качестве опорных берет вторую, третью, пятую и четвертую
вершины Ну и так далее
Если в предыдущем примере поменять константу на CL_QUAD_STRip, как это сделано
в проекте из подкаталога Ex31, то изображение в окне получится таким, как на
рис. 2. 7.
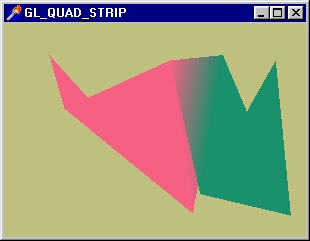
Рис. 2. 7. To же, что и рис 2. 6, но константа GL QUAD STRIP
Для рисования выпуклого многоугольника используется примитив GL_POLYGON. Многоугольник строится из связанных треугольников с общей вершиной, в качестве которой берется первая среди перечисляемых в командных скобках. Код для рисования шестиугольника может выглядеть так:
glBegin (GL_POLYGON);
For i: = 0 to 6 do glVertex2f (0. 5 *cos (2 * Pi * i / 6), 0. 5 * sin (2 * Pi
* i / 6));
glEnd;
Обратите внимание, что в отличие от предыдущих реализаций этой задачи вершины шестиугольника последовательно соединяются не с центром окна, а с крайней правой вершиной, указанной самой первой Это становится хорошо заметным, если менять цвет для каждой вершины, как это сделано в проекте из подкаталога Ex32
Замечание
Для воспроизведения треугольников и четырехугольников лучше не использовать
примитив GL_POLYGON, в таких случаях оптимальным будет использование примитивов,
специально предназначенных для этих фигур
Попробуем чуть усложнить наши построения: зададимся целью нарисовать фигуру, как на рис. 2. 8.

Рис. 2. 8. Невыпуклый многоугольник
Поскольку примитив GL_POLYGON позволяет строить только выпуклые многоугольники,
построение всей фигуры разбиваем на две части, каждая из которых представляет
собой выпуклый многоугольник Соответствующий проект располагается в подкаталоге
ЕхЗЗ, а на рис 2 9 я пометил эти части разными цветами.

Рис. 2. 9. Фигуру для построения разбиваем на несколько частей
Если же попытаться нарисовать эту фигуру "за один присест", то картинка может получиться, например, такой, как на рис 2 10.

Рис. 2. 10. Так выглядит попытка построения фигуры с использованием одной
пары командных скобок
Подкаталог Ex34 содержит проект, в котором эта же фигура строится с использованием
связанных четырехугольников и только одной пары командных скобок. При этом построении
также имеются потери эффективности: некоторые четырехугольники местами строятся
на уже закрашенных местах Для проверки достаточно включить контурный режим рисования
многоугольников, причем при включении такого режима выборочно для лицевой или
изнаночной стороны можно заметить, что одни многоугольники мы видим с лицевой
стороны, а другие - с изнаночной.
Замечание
Важно запомнить: базовые команды OpenGL предназначены для построения только
выпуклых фигур, поэтому сложные фигуры чаще всего рисуются этапами, по частям.
Возможно, вы уже задались вопросом, как нарисовать фигуру с внутренним отверстием.
Подкаталог Ex35 содержит проект для рисования диска, a Ex36 содержит проект,
в котором внутри квадрата рисуется круглое отверстие Всю фигуру разбиваем на
четыре четверти, каждая из которых - группа связанных четырехугольников. Если
включить режим контурного рисования многоугольников, картинка получится такой,
как на рис. 2. 11.

Рис. 2. 11. Так разбивается фигура, если требуется нарисовать внутреннее
отверстие
Если вы имеете опыт работы в графических редакторах, такой подход, возможно, вас несколько разочаровал. Конечно, было бы гораздо удобнее, если бы имелась, например, функция закраски замкнутой области, как это принято в большинстве графических редакторов. Но мы имеем дело с низкоуровневой библиотекой, и она не предоставляет подобных готовых функций.
Замечание
Как мы увидим дальше, есть несколько способов решения задачи построения сложных
объектов - невыпуклых многоугольников или объектов, содержащих отверстия, -
однако самый быстрый (в смысле скорости воспроизведения, а не кодирования) способ
состоит в том, чтобы вы сами полностью расписали алгоритм построения на основе
многоугольников, а в идеале - с использованием только треугольников.
Утешением может стать то, что аппаратные возможности растут стремительно и
подобные рекомендации теряют свою актуальность.
Сейчас самое время обратить ваше внимание на очень важный факт. Если в примере
на отверстие включить режим сглаживания многоугольников:
glEnable (GL_POLYGON_SMOOTH);
то построение фигуры замедляется, что хорошо заметно при изменении размеров окна, когда происходит его перерисовка. Использование режимов, их включение и отключение, может сильно сказаться на скорости воспроизведения, о чем необходимо постоянно помнить.
Команда glEdgeFlag
Режим вывода полигонов (так мы будем иногда называть многоугольники) позволяет
рисовать контуры фигур или только точки в опорных вершинах фигуры. Когда сложная
фигура разбивается на части, контурный режим может испортить картинку: станет
заметным поэтапное построение фигуры. В такой ситуации решение может состоять
в исключении некоторых вершин из построения границы фигуры, что осуществляется
вызовом команды glEdgeFlag. Аргумент этой команды имеет тип Boolean, если точнее
- GLboolean, и мы в главе говорили о небольшой проблеме с этим типом OpenGL.
Как оговаривается в справке, команда дает эффект только в режиме контурного
или поточечного вывода многоугольников. Также специально оговаривается возможность
использования этой команды внутри командных скобок.
Смысл команды следующий: вершины, указываемые после вызова команды с аргументом
False, при построении границы многоугольника не учитываются, как если бы мы
рисовали контур в этом месте прозрачным цветом.
Посмотрите пример, располагающийся в подкаталоге Ex37, в котором наша тестовая
фигура рисуется в двух режимах: полная заливка и контурно. Код при этом выполняется
один и тот же, но для того, чтобы скрыть от наблюдателя секторное разбиение
фигуры, некоторые вершины заключены между строками:
glEdgeFlag (FALSE);
glEdgeFlag (TRUE);
Поэтому при контурном режиме эти вершины просто пропускаются.
Режим вывода многоугольников меняется при нажатии пробела, после чего окно перерисовывается.
В качестве упражнения я бы посоветовал удалить строки, в которых вызывается
команда glEdgeFlag, и посмотреть на получающийся результат.
Массивы вершин
мы рассмотрели все десять примитивов, имеющихся в нашем распоряжении. Код практических
построений, включающих сотни и тысячи отдельных примитивов, подчас чересчур
громоздок, большая часть его в таких случаях - сотни и тысячи строк с вызовом
команды glVertex.
Библиотека OpenGL располагает средством сокращения кода, базирующимся на использовании
массивов вершин. В массиве вершин, т. e. массиве вещественных чисел, задаются
координаты опорных вершин, по которым вызовом одной команды giDrawArrays строится
последовательность примитивов заданного типа.
Поскольку эта команда не входит в стандарт OpenGL и является его расширением
(extension), для получения справки по ней необходимо вызвать контекстную помощьна
слово glDrawArraysEXT.
У команды giDrawArrays три аргумента: тип примитива и характеристики используемого
массива.
Для использования этой функции надо, как минимум, задать массив вершин, по которым
будет строиться множество примитивов. Ссылка на массив вершин создается командой
glvertexPointer, также являющейся расширением стандарта. Помимо массива вершин,
для украшения картинки будем также использовать массив цвета вершин, ссылка
на который задается командой glcolorPointer, тоже не входящей в стандарт. Прибавив
окончание Ехт к именам этих команд, можно получить контекстную подсказку, по
которой легко разобраться с их аргументами. Но, к сожалению, для использования
массива вершин полученной информации недостаточно, необходимо еще использовать,
как минимум, команду glEnableClientstate, справку по которой уже невозможно
получить никакими ухищрениями. Эта команда аналогична glEnable, но применяется
только в контексте массивов вершин У нее имеется парная команда - glDisableclientstate,
отключающая использование массива вершин.
В заголовочном файле opengl. pas, поставляемом с Delphi, отсутствуют прототипы
команд, не входящих в стандарт OpenGL, a также отсутствует описание констант,
используемых такими командами, что немного затруднит наше изучение этой библиотеки.
Обратимся к проекту из подкаталога Ex38.
Массив с именем vertex содержит координаты четырех точек - углов квадрата, а
в массиве цветов Colors содержатся соответствующие вершинам значения RGB:
Vertex: Array [0.. 3, 0.. 1] of GLFloat;
Colors: Array [0.. 3, 0.. 2] of GLFloat;
Код рисования выглядит так:
glVertexPointer(2, GL_FLOAT, 0, @Vertex);
glColorPointer(3, GL FLOAT, 0, @Colors);
// указатель на массив вершин
// указатель на массив цветов
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);
glDrawArrays(GL_POLYGON, 0, 4);
glDisableClientState(GL_COLOR_ARRAY);
glDisableClientState(GL_VERTEX_ARRAY);
// массив вершин - включаем режим
// массив цветов - включаем режим
// рисование множества полигонов
// выключаем режимы (в этом
// примере не обязательно)
Значение первого аргумента команды glvertexPointer равно двум, поскольку вершины
заданы указанием двух координат. To есть этот аргумент задает, по сколько вещественных
чисел считывать для каждой точки.
Результат работы программы показан на рис. 2 12.
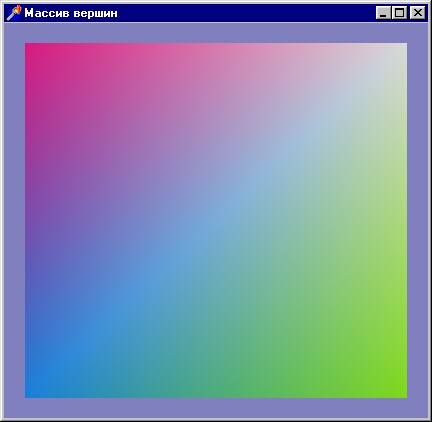
Рис. 2. 12. Иллюстрация к примеру на использование массива вершин
Для использования команд-расширений программу пришлось дополнить строками с описанием прототипов процедур:
procedure glVertexPointer (size: GLint; atype: GLenum;
stride: GLsizel; data: pointer);
stdcall;
external OpenGL32;
Procedure glColorPointer (size: GLint; atype: GLenum; stride: GLsizei;
data: pointer);
stdcall;
external OpenGL32;
procedure giDrawArrays (mode: GLenum; first: GLint; count: GLsizei);
stdcall;
external OpenGL32;
Procedure glEnableClientState (aarray: GLenum);
stdcall;
external OpenGL32;
Procedure glDisableClientState (aarray: GLenum);
stdcall;
external CpenGL32;
OpenGL32- константа, определяемая в модуле opengl. pas. Потребовалось также задать значение констант, используемых этими процедурами:
const
GL_VERTEX_ARRAY = $8074;
GL__COLOR_ARRAY = $8076;
Значения констант и информацию о типах аргументов процедур я почерпнул из заголовочных
файлов сторонних разработчиков и перепроверил по содержимому файла gl. h, поставляемым
с Visual C++. Информация о команде glEnableclientstate взята из описания OpenGL
фирмы SGI.
Первым аргументом giDrawArrays может быть любая константа, которую допускается
использовать в glBegin. Чтобы лучше разобраться с принципом построения, рекомендую
посмотреть результат работы программы с использованием отличных от GL_POLYGON
констант.
В примере по массиву вершин строится множество полигонов вызовом команды
glDrawArrays(GL POLYGON, 0, 4); // рисование множества полигонов
Эта команда является сокращением следующей последовательности команд (пример из подкаталога Ex39):
glBegin (GL_POLYGON);
glArrayElement(0);
glArrayElement(1);
glArrayElement(2);
glArrayElement(3);
glEnd;
Используемая здесь функция glArrayElement (также расширение стандарта) берет
в качестве вершины примитива элемент массива с заданным индексом. Индекс, как
видно из примера, начинается с нуля.
В продолжение этой темы разберите также проект из подкаталога Ex40 - мою адаптацию
и трансляцию под Delphi программы Polygons из книги [1], результат работы которой
иллюстрирует рис. 2. 13.

Рис. 2. 13. Уже сейчас вы умеете создавать высококачественные изображения
вы возможно, задаетесь вопросом, почему в заголовочном файле, поставляемом
с Delphi, отсутствуют прототипы процедур, хоть и не входящих стандарт OpenGL,
но документированных разработчиком библиотеки. Ответ на этот вопрос заключается,
по-видимому, в том, что этот файл является трансляцией заголовочных файлов gl.
h и glu. h, опубликованных SGI, и в него вошло только то, что документировано
в этих файлах. Как явствует из заголовка файла, за основу положены файлы версии
1993 года.
Помимо массивов вершин и массива цветов вершин, имеется массив границ - аналог
команды glEdgeFlag применительно к массивам вершин.
В этом случае необходимо использовать команду glEdgeFlagpointer. Прибавив суффикс
Ехт, вы можете получить справку по этой команде. В ней, в частности, говорится,
что включение режима использования массива границ осуществляется так:
glEnable (GL_EDGE_FLAG_ARRAY_EXT);
Однако это указание, по-видимому, является ошибочным. Я смог воспользоваться массивом флагов границ только с использованием следующего кода:
glEnableClientState (GL_EDGE_FLAG_ARRAY);
To же самое я могу сказать по поводу аргументов команды.
Посмотрите проект из подкаталога Ex41, где для иллюстрации используется все
та же тестовая фигура, изображенная на рис. 2. 8. В этом примере фигура выводится
с использованием команды giDrawArrays в двух режимах - сплошной заливкой и контурно.
При втором режиме сказывается действие подключения массива границ.
В коде программы добавился прототип процедуры glEdgeFlagPointer. Обратите внимание
на расхождение в описании прототипа с документацией: У прототипа два аргумента
вместо трех. Если попытаться в точности следовать документации, в результате
либо не используется массив границ, либо возникает сообщение об ошибке.
Прямое обращение к пикселам экрана
Библиотека OpenGL располагает командами, позволяющими осуществить непосредственный
доступ к пикселам экрана. Разберем проект из подкаталога Ex42 - простой пример
на вывод блока пикселов на экран вызовом двух команд:
glRasterPos2f (-0. 25, -0. 25);
glDrawPixels(ImageWidth, ImageHeight, GL_RGB, GL_UNSIGNED_BYTE, @Image);
Первая команда задает базовую точку для выводимого блока, вторая ocyществляет
собственно вывод массива пикселов. Высота при выводе может и отличаться от реального
размера массива, т е быть меньше, ширину же для корректного вывода желательно
не брать меньше действительного размера массива.
В этом простом примере выводимый массив заполняется значениями RGF так, что
в результате получается шахматная доска с сине-красными клетками
const
ImageWidth = 64;
ImageHeight = 64;
...
Image : Array [0..ImageHeight-1, 0..ImageWidth - 1, 0..2] of GLUbyte;
...
{=================================================
Создание образа шахматной доски}
procedure TfrmGL.Makelmage;
var i, j : Integer;
begin For i := 0 to ImageHeight - 1 do
For з := 0 to ImageWidth - 1 do begin
If ((i and 8) = 0) xor ( (j and 8) = 0)
then begin
Image[ i ] [ j ][ 0 ] :=0; // красный
Image [ i ] [ j ][1] : = 0; // зеленый
Image[i][j][2] := 255; // синий
end
else begin
Image[ i ] [ j ][0] := 255; // красный
Image[ i ][ j ][1] := 0; // зеленый
Image[ i ] [ j ][2] := 0; // синий
end;
end;
end;
В развитие темы разберем более интересный пример (подкаталог Ех43), где выводимый массив заполняется следующим образом" создается объект класса TBitmap, в который загружается растр из bmp-файла, последовательно считываются пикселы объекта, и в соответствии со значениями цвета каждого пиксела заполняются элементы массива. Все просто, только надо обратить внимание, что ось Y битовой карты направлена вниз, поэтому элементы массива заполняются в обратном порядке:
procedure TfrmGL.Makelmage;
var
i, ] : Integer;
PixCol : TColor;
Bitmap : TBitmap;
begin
Bitmap := TBitmap.Create;
Bitmap.LoadFromFile ('Claudia.bmp');
For i := 0 to ImageHeight - 1 do For ] := 0 to ImageWidth - 1 do begin
PixCol := Bitmap.Canvas.Pixels [j, i];
// перевод цвета из TColor в цвет для команд OpenGL
Image[ImageHeight - i - 1][3][0] := PixCol and $FF;
Image[ImageHeight - i - 1] [3] [1] := (PixCol and $FFOO) shr 8;
Image[ImageHeight - i - 1][3][2] := (PixCol and $FFOOOO) shr 16;
end,
Bitmap.Free;
end;
Обратите внимание на строку, задающую выравнивание пикселов - без нее массив пикселов будет выводиться некорректно
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
Возможно, при знакомстве с файлом справки вы обратили внимание на команду giBitMap, специально предназначенную для вывода битовых массивов Растр в таком случае может быть монохромным, а не 24-битным Обычно эта команда используется для вывода текста, мы рассмотрим ее в главе 6. Выводимые массивы пикселов легко масштабируются вызовом команды giPixeizoom, аргументы которой - масштабные множители по осям X и Y. Для иллюстрации посмотрите проект из подкаталога Ех44, где нажатием клавиш 'X' и 'Y' можно управлять масштабом по соответствующим осям Обратите внимание, что при отрицательном значении множителей изображение переворачивается по соответствующей оси тот пример демонстрирует также еще одно возможное использование команды glPixelStorei, позволяющей, в частности, прокручивать изображение по вертикали или горизонтали, что в нашей программе осуществляется нажатием клавиш 'R'1 и 'P'1
Замечание
Учтите, что при прокрутке изображения на величину, превышающую половину растра,
происходит аварийное завершение программы.
Команда glCopyPixeis позволяет копировать часть экрана в текущей позиции задаваемой
giRasterpos объекте из диалога Ех45 я воспользовался этой командой следующим
образом при нажатой кнопке мыши вслед за указателем мыши перемещается копия
левого нижнего угла экрана. Изображение восстанавливается при каждой перерисовке
экрана.
Здесь надо обратить внимание, что, в отличие от всех остальных примеров данной
главы, флаги окна не включают двойную буферизацию и что контекст воспроизведения
занимается приложением сразу по началу работы и не освобождается до завершения
работы. Обработка движения мыши заканчивается не перерисовкой окна, а командой
glFlush.
Команда glPixelTransfer позволяет задавать режимы вывода пикселов, в частности,
задавать цветовые фильтры. В примере, располагающемся в подкаталоге Ex46, нажатием
клавиш 'R', 'G', 'B' можно изменить составляющую долю соответствующего цвета.
Замечание
Надо отметить, что команды непосредственного доступа к пикселам экрана работают
сравнительно медленно, поэтому используются только в исключительных случаях.
Команда glReadPixels позволяет считывать содержимое всего экрана или части
его. Это одна из самых важных для нас команд, мы еще неоднократно будем к ней
обращаться.
Для иллюстрации ее работы я подготовил проект (подкаталог Ex47), выводящий на
экран простейшие стереокартинки. Одна из них показана на рис. 2. 14.

Рис. 2. 14. Если вы умеете смотреть на стереокартинки, то увидите здесь парящий квадрат. Картинка рассчитана на размеры монитора, не ручаюсь, что в лекциях эффект повторится
В примере реализован следующий алгоритм: экран заполняется множеством маленьких черно-белых квадратиков, создающих хаос. Затем небольшая обасть экрана размером 50x50 пикселов считывается в массив и последовательно копируется восемь раз, в две строки по четыре квадрата впритык. Вот фрагмент кода для первой копии:
Pixel: Array [0.. 50, 0.. 50, 0.. 2] of GLUbyte;
// считываем в массив часть образа экрана вблизи центра
glReadPixels(round(ClientWidth / 2), round(ClientHeight / 2), 50, 50,
GL_RGB, GL_UNSIGNED_BYTE, @Pixel);
glRasterPos2f (-0. 5, 0. 0); // устанавливаем точку вывода
glDrawPixels(50, 50, GL_RGB, GL_UNSIGNED_BYTE, @Pixel}; // вывод копии
В принципе, достаточно однократного копирования, но тогда требуется особое
мастерство для того, чтобы увидеть объемное изображение. Чтобы скрыть уловку,
можно еще набросать на экране немного точек или линий, но разглядеть после этого
спрятанный квадрат становится труднее.
При нажатии клавиши <пробел> экран перерисовывается, так что у вас есть
возможность подобрать наиболее удачную картинку.
Команда glGetString
Вы, наверное, обратили внимание, изучая справки по командам-расширениям, что
приложение может получить информацию об имеющихся расширениях OpenGL с помощью
команды glGetstring. Из соответствующей справки выясняем, что результат работы
команды - строка типа Pchar, а аргументом может быть одна из четырех констант.
В зависимости от используемой константы строка содержит информацию о фирме-производителе
или способе воспроизведения, версии OpenGL и имеющихся расширениях стандарта.
На основе использования этой функции построен пример, располагающийся в подкаталоге
Ex48. Результат работы программы представлен на рис. 2. 15.
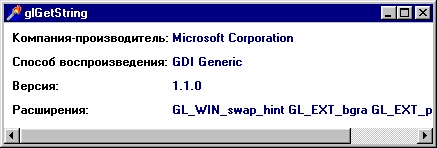
рис. 2. 15. Пример получения информации с помощью команды glGetString
При разборе программы обратите внимание на две вещи:
Этот пример дает еще одну подсказку, как распознать наличие графического акселератора:
при отсутствии такового glGetstring с аргументом GL_RENDERER возвращает строку
'GDI Generic'.
В файле справки можно также прочитать, что glGetstring с аргументом GL_EXTENSiONS
возвращает строку, где через пробел перечисляются поддерживаемые текущим соединением
расширения.
В частности, согласно документации, командой glDrawArrays можно пользоваться,
только если в расширениях присутсвует GL_EXT_vertex_array. Это одно из спорных
мест, потому что я с успехом применяю расширение массива вершин, хотя в указанном
списке ссылка на его наличие отсутствует Поэтому я бы не советовал полностью
доверяться возвращаемому списку Не стоит и в программах сразу же прекращать
выполнение, если вы опираетесь на расширение стандарта OpenGL, которое не определяется.
По-моему, в такой ситуации достаточно просто предупредить пользователя о возможных
сбоях в работе программы.
Обработка ошибок
Использующее OpenGL приложение по ходу работы может выполнять некорректные действия,
приводящие к ошибкам в работе Часть ошибок носит фатальный характер, ведущий
к аварийному завершению работы приложения Другие могут и не приводить к такому
финалу, но код воспроизведения, содержащий ошибку, не выполняется. Пример такой
ошибки, который я уже приводил - неверная константа в качестве аргумента функции
glBegin или неверное количество вершин для воспроизведения примитива Конечно,
компилятор не может и не должен распознавать подобные ошибки, но и OpenGL не
может отработать такие указания клиента В документации по OpenGL к каждой команде
прикладывается раздел "Errors", содержащий указания, какие ошибки
могут возникнуть при использовании этой команды.
Команда OpenGL glGetError возвращает информацию об ошибке в виде оД-ной из семи
констант Обратите внимание, что в свою очередь эта команда сама может генерировать
ошибку, если вызывается внутри командных скобок OpenGL.
На использовании этой функции построен пример, располагающийся в подкаталоге
Ex49 В программе из-за заведомо неверного аргумента функции giBegm генерируется
ошибка библиотеки
OpenGL типа GL_iNVALiDENUM
Соответствующее сообщение выводится в заголовке окна, использовать диалоговые окна в такой ситуации нежелательно, поскольку это приведет к перерисовке окна, т e снова будет сгенерирована ошибка В программе также введена пользовательская функция, возвращающая строку с описанием ошибки:
function GetError: String;
begin Case glGetError of
GL__INVALID_ENUM: Result: = 'Неверный аргумент1';
GL INVALID_VALUE: Result: = 'Неверное значение аргумента1';
GL INVALID_OPERATION: Result: = 'Неверная операция1';
GL STACK_OVERFLOW: Result: = 'Переполнение стека1';
GL STACK_UNDERFLOW: Result: = 'Потеря значимости стека'';
GL OUT OF_MEMORY: Result: = 'He хватает памяти1';
GL_NO_ERROR: Result: = 'Нет ошибок. ';
end;
end;
Масштабирование
Мы уже знаем, что границы области вывода лежат в пределах от -1 до 1 Это может
привести к неудобству при подготовке изображений К счастью, OpenGL предоставляет
удобное средство на этот случай - масштабирование
Разберем его на примере программы построения фигуры, показанной на рис 2. 8.Для
изменения масштаба используется команда glScalef с тремя аргументами, представляющими
собой масштабные множители для каждой из осей.
Например, если перед командными скобками вставим строку
glScalef (0. 5, 0. 5, 1. 0);,
то будет нарисована уменьшенная в два раза фигура (готовый проект располагается в подкаталоге Ex50).После команд рисования необходимо восстановить нормальный масштаб, т. e в данном случае добавить строку:
glScalef (2. 0, 2. 0, 1. 0);.
Есть и другой способ запоминания/восстановления текущего масштаба, но о нем
мы поговорим позднее. Восстанавливать масштаб необходимо для того, чтобы каждое
последующее обращение к обработчику перерисовки экрана не приводило бы к последовательному
уменьшению/увеличению изображения В принципе, можно ис- пользовать и флаги для
того, чтобы обратиться к строке единственный раз в ходе работы приложения.
Масштабные множители могут иметь отрицательные значения, при этом изображение
переворачивается по соответствующей оси. Иллюстрирующий это свойство проект
находится в подкаталоге Ex51.
При двумерных построениях значение коэффициента по оси Z безразлично, единица
взята без особых соображений.
Поворот
Для поворота используется команда glRotatef с четырьмя аргументами: угол поворота,
в градусах, и вектор поворота, три вещественных числа.
Для двумерных построений наиболее нагляден поворот по оси Z, чем я и пользуюсь
в приводимых примерах.
В предыдущем примере перед командными скобками вставьте строку:
glRotatef (5, 0. 0, 0. 0, 1. 0);
и создайте обработчик события Keypress с единственной командой Refresh. Теперь
при нажатии любой клавиши окно перерисовывается, при этом каждый раз фигура
поворачивается на пять градусов по оси Z (проект из подкаталога Ex52).
Здесь надо обратить внимание на две вещи: на то, что при положительном значении
компоненты вектора поворот осуществляется против часовой стрелки и то, что важно
не само значение компоненты, а ее знак и равенство/неравенство ее нулю.
Хотя мы пока ограничиваемся плоскостными построениями, поворот по любой из осей
сказывается на воспроизводимой картинке. Проверьте: при повороте по осям X и
Y мы получаем правильную картинку в проекции с учетом поворота по осям.
Поворот часто используется при построениях, поэтому важно разобраться в нем
досконально. Точно так же, как было с масштабом, поворот действует на все последующие
команды воспроизведения, так что при необходимости текущее состояние восстанавливается
обратным поворотом.
Например, если надо нарисовать повернутый на 45 градусов квадрат, т e. ромб,
то код должен выглядеть так (готовый проект можете взять в подкаталоге Ex53):
glRotatef (45, 0. 0, 0. 0, 1. 0);
glBegin (GL_POLYGON);
glVertex2f (-0. 6, -0. 1);
glVertex2f (-0. 6, 0. 4);
glVertex2f (-0. 1, 0. 4);
glVertex2f (-0. 1, -0. 1);
glEnd; lRotatef (-45, 0. 0, 0. 0, 1. 0);
Этот пример очень занимателен и вот почему. Удалим восстановление угла поворота
и запустим приложение. Увидим не ромб, а квадрат. При внимательном рассмотрении
обнаружим, что квадрат был повернут дважды Произошло это потому, что сразу после
появления окна на экране (функция API showWindow) происходит его перерисовка
(функция API updateWindow). Если вы были внимательны, то могли заметить, что
такой же эффект наблюдался и в предыдущем примере.
При выполнении операции поворота можно спросить: поворачивается изображение
или точка зрения? Мы будем для ясности считать, что поворачивается именно изображение.
Следующий пример пояснит это.
Замечание
Точный ответ такой все объекты в OpenGL рисуются в точке отсчета системы координат,
а команда glRotate осуществляет поворот системы координат.
Нарисуем две фигуры: квадрат и ромб, причем ромб получим путем поворота квадрата.
Текст программы будет такой (проект из подкаталога Ex54):
glRotatef (45, 0. 0, 0. 0, 1. 0);
glBegin (GL_POLYGON);
glVertex2f (-0. 6, -0. 1);
glVertex2f (-0. 6, 0. 4);
glVertex2f (-0. 1, 0. 4);
glVertex2f (-0. 1, -0. 1);
glEnd;
glRotatef (-45, 0. 0, 0. 0, 1. 0);
glBegin (GL_POLYGON);
glVertex2f (0. 1, -0. 1);
glVertex2f (0. 1, 0. 4);
glVertex2f (0. 6, 0. 4);
glVertex2f (0. 6, -0. 1);
glEnd;
Точно так же нам придется поступать всегда, когда на экране присутствует несколько
объектов, повернутых относительно друг друга: перед рисованием очередного объекта
осуществлять поворот, а после рисования - возвращать точку зрения или осуществлять
следующий поворот с учетом текущего положения точки зрения.
Пожалуйста, будьте внимательны! Начинающие пользователи OpenGL пoстоянно задают
вопрос, как повернуть примитив, не поворачивая остальные примитивы. Еще один
раз перечитайте предыдущий абзац В заключение разговора о повороте рассмотрите
проект (подкаталог Ex55) основанный на примере с диском. При нажатой кнопке
или движении кур, сора происходит перерисовка окна и поворот диска на 60 градусов.
Чтобы вы могли оценить преимущества использования "низкоуровневых"
приемов, окно перерисовывается в этих случаях по-разному:
procedure TfrmGL. FormKeyPress(Sender: TObject; var Key: Char);
begin
Refresh
end;
procedure TfrmGL. FormMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
InvalidateRect(Handle, nil, False);
end;
При нажатии кнопки хорошо видно мерцание на поверхности окна, которого не появляется при движении указателя мыши по его поверхности.
Перенос
Перенос точки зрения (системы координат) осуществляется командой glTranslatef
с тремя аргументами - величинами переноса для каждой из осей.
Все сказанное по поводу восстановления точки зрения справедливо и в отношении
переноса.
Рассмотрите пример из подкаталога Ex56, иллюстрирующий использование переноса
системы координат. Думаю, особых пояснений здесь не потребуется, поэтому перейдем
к вопросу о совместном использовании поворота и переноса - это чаще всего и
используется при построениях. Программа из подкаталога Ex57 строит узор, показанный
на рис. 2. 16.
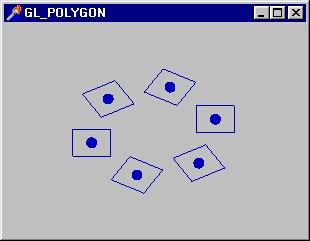
Рис. 2. 17. Еще один пример на поворот и перенос
Стоит разобрать этот пример подробнее. В цикле шесть раз происходит перенос
и поворот системы координат:
glTranslatef (-0. 3, 0. 3, 0. 0);
glRotatef (60, 0, 0, 1);
Кружочки рисуются в текущей точке отсчета системы координат, относительно которой происходят каждый раз преобразования. По завершении цикла точка зрения возвращается точно в начальное положение, поэтому дополнительных манипуляций с системой координат не требуется. Перед циклом делаем перенос для выравнивания картинки на экране:
glTranslatef (0. 4, 0. 1, 0. 0);
После цикла, конечно, требуется восстановить первоначальное положение системы координат:
glTranslatef (-0. 4, -0. 1, 0. 0);
Разобравшись с этим примером, перейдите к примеру, располагающемуся в следующем подкаталоге, Ex58. Здесь строятся шесть квадратов по кругу, как показано на рис. 2. 17.

Рис. 2.17. Еше один пример на поворот и пепренос
Как и все предыдущие, этот пример тоже не отличается особой сложностью. В цикле
перед рисованием очередного квадрата смешаем и поворачиваем систему координат:
glTranslatef (-0. 7 * cos (Pi * i / 3), 0. 7 * sin (Pi * i / 3), 0. 0);
glRotatef (-60 * i, 0, 0, 1);
а после рисования очередного квадрата делаем обратные действия:
glRotatef (60 * i, 0, 0, 1);
glTranslatef (0. 7 * cos (Pi * i / 3), -0. 7 * sin (Pi * i / 3), 0. 0);
Все, надеюсь, просто и понятно. Здесь только надо хорошенько уяснить, что порядок манипуляций с системой координат поменять нельзя: вначале пе-ренос, затем поворот, по окончании рисования - в обратном порядке: поворот, затем перенос. Если поменять порядок в любой из пар этих действий либо в обеих парах, будет рисоваться другая картинка - обязательно проверьте это самостоятельно.
Сохранение и восстановление текущего положения
По предыдущим примерам вы должны были очень хорошо уяснить, на-cколько важно
восстанавливать текущую систему координат. При каждой следующей перерисовке
окна она сдвигается и поворачивается, поэтому нам приходится постоянно следить,
чтобы после рисования система координат вернулась в прежнее место. Для этого
мы пользовались обратными поворотами и перемещениями. Такой подход неэффективен
и редко встречается в примерах и профессиональных программах, т. к. приводит
к потерям скорости воспроизведения. Если вы прочитаете справку по функциям glRotatef
и glTranslatef, то узнаете, что эти функции реализуются как перемножение текущей
матрицы на матрицы поворота и переноса, соответственно.
Обычно в состоянии, к которому потребуется затем вернуться, запоминают значение
текущей матрицы. Вместо того чтобы заново перемножать матрицы и тратить время
на операции, связанные с математическими расчетами, возвращаемся сразу к запомненному
значению.
Команды glPushMatrix и glPopMatrix позволяют запомнить и восстановить текущую
матрицу. Эти команды оперируют со стеком, то есть, как всегда в подобных случаях,
можно запоминать (проталкивать) несколько величин, а при каждом восстановлении
(выталкивании) содержимое стека поднимается вверх на единицу данных.
Использование этих функций делает код более читабельным, а воспроизведение -
более быстрым, поэтому во всех оставшихся примерах мы, как правило, не будем
производить малоэффективные действия по обратному перемножению матриц, а будем
опираться на использование рассмотренных команд.
Для большей ясности рассмотрите пример из подкаталога Ex59 - модификацию примера
на шесть квадратов. В цикле перед операциями поворота и переноса запоминаем
текущую систему координат (обращаемся к glpushMatrix), а после рисования очередного
квадрата - восстанавливаем ее (вызываем giPopMatrix). Надеюсь, понятно, что
в стек помещается и извлекается из него пять раз одна и та же матрица, причем
в этой программе в стеке содержится всегда не больше одной матрицы.
Библиотека OpenGL позволяет запоминать и возвращать не только текущую систему
координат, но и остальные параметры воспроизведения.
Посмотрите документацию по функции glGet, а конкретно, список модификаций этой
функции, различающихся по типу аргумента в зависимости от запоминаемого параметра.
Обратите внимание, что второй аргумент функции - всегда указатель на переменную
соответствующего типа, поэтому все функции заканчиваются на "v". Первый
аргумент - символическая константа, указывающая, какой параметр запоминаем.
Закрепим изученный материал разбором проекта из подкаталога Ex60. Рисуем три
точки, первую и третью одинаковым цветом. Код следующий:
glColor3f (1. 0, 0. 0, 0. 0);
glGetFloatv (GL CURRENT COLOR, @Color);
glBegm (GL_POINTS);
glVertex2f (-0. 25, -0. 25);
glColor3f (0. 0, 0. 0, 1. 0);
glVertex2f (-0. 25, 0. 25);
glColor3f (Color [0], Color [1], Color [2]);
glVertex2f (0. 25, 0. 25);
glEnd;
Для сохранения текущего цвета используется переменная color типа TGLArrayf3 (массив трех вещественных чисел). В качестве пояснения напомню, что вторым аргументом glGet должен быть указатель на переменную, в которой сохраняется значение параметра.
Первые шаги в пространстве
Во всех предыдущих примерах для задания вершин мы использовали версию команды
glvertex с указанием двух координат вершин. Третья координата, по оси Z, устанавливалась
нулевой.
Для дальнейшего знакомства с OpenGL нам необходимо выяснить одну важную вещь,
для чего попробуем рисовать примитивы с заданием третьей координаты, не равной
нулю.
Взгляните на пример из подкаталога Ex6l. Здесь рисуется треугольник со значением
координаты вершин по Z равным текущему значению переменной h. При нажатии клавиш
<пробел>+<Shift> значение этой переменной увеличивается на единицу,
если нажимать просто <пробел>, то значение переменной на единицу уменьшается.
Значение переменной выводится в заголовке окна. После этого картинка перерисовывается.
Поработав с этим примером, вы можете обнаружить, что пока координата по оси
Z не превышает по модулю единицу, треугольник виден наблюдателю. Вы можете уменьшить
шаг изменения переменной h, чтобы повысить достоверность вывода, но результат
окажется таким же: как только примитив выходит за пределы воображаемого куба
с координатами вершин, имеющими по модулю единичное значение, примитив перестает
быть видимым.
Точнее, нам становится не видна часть примитива, выходящая за пределы этого
куба. В примере из подкаталога Ex62 мы манипулируем координатой только одной
из вершин треугольника, остальные не перемещаются и располагаются точно на плоскости.
При движении третьей вершины в пространстве мы видим только ту часть треугольника,
которая помещается в куб.
Этот пример иллюстрирует еще одну важную вещь. Помимо треугольника, здесь строится
квадрат. Первым строится квадрат, вторым - треугольник. Треугольник частично
перекрывает квадрат так, как если бы он был нарисован сверху. Если поменять
порядок рисования примитивов, квадрат рисуется "выше" треугольника.
Замечание
Итак, OpenGL воспроизводит только те части примитивов, координаты которых не
превышают по модулю единицу. Примитивы с одинаковыми координатами рисуются по
принципу "каждый последующий рисуется поверх предыдущего". Если вы
не теряли внимание по ходу наших уроков, то должны были убедиться в правильности
второго вывода, еще разбираясь с примером на связанные четырехугольники
Последний пример этой главы достоин того, чтобы разобраться с ним подробнее.
Обратите внимание, что при отрицательном значении переменной h треугольник строится
все равно "выше" квадрата, т. e. пока мы не можем получить действительно
пространственных построений, учитывающих взаимное положение примитивов в пространстве.
|
|