Замечательные эксперименты Кауфмана по электрическому и магнитному отклонению бета-лучей радия приводят к убеждению, что масса частиц или электронов зависит от их скорости и полностью электромагнитной природы. Существование их электрической инерционности и изменчивости со скоростью предполагалась теорией, которая на первый взгляд кажется получила замечательное подтверждение. Тем не менее при рассмотрении области применимости этих выводов желательно проанализировать являются ли они совершенно необходимыми.
Давайте вернемся к тому, что в этих экспериментах бета-луч одновременно подвержен действию электрического поля E, производящего отклонение y, и в магнитного поля H параллельного E, производящего отклонение z перпендикулярное первому. Фотографическая пластинка, перпендикулярная неотклонённому лучу, регистрирует интенсивность луча и позволяет произвести прямомые измерения y и z. Если m - масса, v - скорость электрона, e - его заряд, a и b две константы прибора, то, согласно теории Лоренца, Радий в определенных пределах выдает бета-лучи всех скоростей.
![]()
Эти уравнения, где v играет параметрическую роль, представляют определенную параболу, если m не зависит от v. Но на кривой, полученной Кауфманом - другое. Это явление может быть объяснено по-разному.
1. Согласно Лоренцу, перемещение электрически заряженного тела по отношению к эфиру является эквивалентом электрическому току, чье поле, благодаря эффекту, аналогичному самоиндукции, реагирует на тело и производит усилие, которое в наиболее общей гипотезе является линейной функцией ускоряющихся частиц, а коэффициенты (для поперечной и продольной массы) являются функциями, определяемыми абсолютной скоростью v известной, например, для сферы и эллипсоида. В случае экспериментов Кауфмана, играет роль только поперечная масса μ(v). Если использовать μ(v) в функции (16) вместо m, то можно получить очень точную аппроксимацию наблюдаемой кривой, рассматриваем ли мы электрон как жесткую сферу (Абрахам [Abraham]), или же считаем, что только его объем является постоянным (Бюхерер, Ланжевен [Bucherer и Langevin]).
Чтобы оценить важность такой интерпретации, давайте вспомним, что вычисление электродинамической массы однозначно соотносится к движению электрически заряженного тела по отношению к эфиру, позиция и скорость других тел являются несущественными. Это абсолютная скорость тела, которая используется в формуле. Такая интерпретация эксперимента Кауфмана будет, следовательно, первой для того, чтобы подтвердить наличие абсолютного движения. Теперь, относительно такого деликатного вопроса, как теория Лоренца, которая по крайней мере в той форме, как это изложено в разделе 1, несогласуется с экспериментом, и это расхождение переносится в конкретное выражение электромагнитной движущей силы G, из которой Абрахам вывел величины для продольных и поперечных масс. На самом деле, из вычисления G, которое мы выводим [1], для случая заряженного конденсатора, передвигаемого вдоль движения Земли, возникает впечатление существования пары второго порядка, действующей на конденсатор. Но Троутон и Нобель (Trouton, Noble), которые делали этот эксперимент [2], не наблюдали эту пару. Следовательно величина G не зависит от абсолютной скорости или, по крайней мере не так, как в теории Лоренца. Отсюда мы должны заключить, что, даже если бы согласие между теорией Абрахама с экспериментами Кауфмана было бы превосходным, эта теория должна тем не менее считаться сомнительной.
2. В борьбе за устранение влияния абсолютного движения в своих уравнениях Лоренц пришел к определенным новым гипотезам, к которым я возвращусь в следующем разделе. Размеры электронов, в частности, должны уменьшаться до величины (1-v2/c2)-1/2, когда он разогнан до абсолютной скорости v. Эта гипотеза привела к новым формулам для массы, которые Кауфман считал несовместимыми с его последними экспериментами [3]. Но этот вывод кажется мне сомнительным. На самом деле, давайте примем за H, E, a, b, непосредственно наблюдаемые величины, где вместо величины![]()
![]()
затем Абрахама
![]()
и, наконец, того же Лоренца
![]()
Это означает умножение на коэффициенты 1, 1.040, 1.070 и 1.130, абсцисс и ординат, вычисленных Кауфманом для (см. цит., стр. 534). Мы таким образом находим три кривых для которых ошибки находятся в пределах ошибки эксперимента, как мы можем убедиться глядя на отображение этих величин на кривой фиг.11 Кауфмана. Этот ученый сделал прямые наблюдения и затем, используя метод наименьших квадратов, вывел из различных предлагаемых формул очевидную константу: E/Mc, независимую от гипотез разработанных для e/mo. Формула Лоренца даёт недопустимую величину. Наши вычисления показывают, что величина E/Mc, определенная таким способом, включает значительную неопределенность, для взятых нами непосредственно наблюдаемых величин, ошибки, происходящие из этого, будут превосходить допустимую величину.
Что касается величины
![]()
ее приложение к бета-распаду радия может не быть разрешено, как это вообще не применимо к эффекту Зеемана. Короче говоря, эти наблюдения не дают предпочтения к любой из этих формул перед другими, и это легко показать.
Однако, важно видеть, что новые гипотезы Лоренца, включающие модификацию в выражении для силы, которая возникает, когда два движущихся заряженных тела оказывают влияние друг на друга, как показано на простом примере, ощутимы только для скоростей сравнимых со скоростью света. То есть только для эксперимента Кауфмана.
3. Это ведет к следующему общему замечанию. Можно легко ввести условия, представляющие эту особенность в уравнения электродинамики. Так что система уравнений с (I) по (IV) может быть заменена элементарными действиями, и это будет достаточно для их рассмотрения здесь. Теперь усилие, оказанное частицей e', имеющей скорость v', на частицу e, имеющую скорость v, выражается при этом последнем подходе в линейной форме фактора 1/c2, что выражается для последнего случая в однородном движении, данном в очень усложненной форме Шварцшильдом. Мы видeли в разделе 6, что член первого порядка для условия расширения v'/c - мал. Асиметрия, установленная ранее между v и v' не подтверждается экспериментом, и, как мы увидим во второй части, возникает бесконечность в формулах, содержащих только относительные скорости и следовательно, отличие от тех же самых условий Лоренца. Было бы более оправданным добавить условия, содержащие v/c, третьего и четвертого порядков, без которых формулы не могут отвечать всем экспериментам при малых v/c. Элементарные формулы Лоренца могут служить только для первого приближения. Мы сможем избавиться от произвольной функции v таким образом введенной в (16) для того, чтобы сохранить согласие с экспериментами Кауфмана и гипотезой о постоянстве массы, и до некоторой степени с тем, чтобы полностью сохранить относительность движения. Это будет показано более детально во второй части этой работы.
Но есть более важное. Сама форма кривой, и существование точки, где отклонения y и z - недействительны, и равны скорости c, остается сомнительным. На самом деле, давайте предположим, что
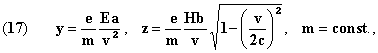
откуда мы получаем параболу
![]()
Поскольку, согласно Лоренцу, для m = const мы имеем сравнимую параболу
![]()
![]()
y' calc. - y' obs.
z' y' obs. I. II.
0.1350 0.0246 +0.0015 +0.0014
0.1919 0.0376 -0.0011 -0.0009
0.2400 0.0502 -0.0022 -0.0018
0.2890 0.0645 -0.0020 -0.0011
0.3359 0.0811 -0.0020 -0.0007
0.3832 0.1001 -0.0025 -0.0008
0.4305 0.1205 -0.0015 -0.0010
0.4735 0.1405 +0.0002 +0.0030
0.5252 0.1667 +0.0025 +0.0063
Различие между разными индивидуальными величинами y', наблюденными Кауфманом и кривой, которая представляет среднее для его экспериментов часто больше, чем 0.0030. Следовательно, ошибки третьей колонки, хотя систематические, могут считаться допустимыми. Те же в четвертой колонке, что соотносятся с гипотезой - полностью объяснимы как экспериментальные ошибки, за исключением последних двух. Но мы должны иметь в виду, что однопроцентная ошибка в абсолютном измерении магнитного поля, которая может очень легко возникнцть при накоплении ошибок, которые сопровождают различные наблюдения, необходимые для этого эксперимента, была бы особенно значительной в этих двух примерах и изменять их y' до 2%, то есть, до величины 0.0034. Эти последние точки были наблюдены только два раза, и измерения Кауфмана, от которых мы отклонились в концах кривой, где интенсивность слаба, чтобы принимать во внимание ее касательную там, где она составляет величину слишком малую для y'. Этих двух соображений было бы достаточно, чтобы объяснить ошибки в четвертой колонке. Но, на этой кривой для (17) скоростью света c не является такой критичной, как максимальная относительная скорость 2c двух лучей света в пределах той же фиксированной системы, для которой нет ничего удивительного в теории, которая рассматривает только относительные скорости.
Магнитная девиация z' в этой точке равна нулю, но не электрическая, которая всегда равна половине ширины (0.03) кривой. Мы видим, что произвольное расширение поля является пищей для гипотез. В заключение, позвольте заметить, что скорость v просто выполняет параметрическую роль, и определяется в каждой точке кривой посредством наблюдаемых величин y и z. Результат будет различным в зависимости от использованной теории, и мы можем представить кривую бесконечным множеством направлений по данному параметру. Это случилось бы и в противном случае, если прямые и точные эксперименты, как например, те что выполнены де-Кудре (Des Coudres) и Вихертом (Wiechert) посредством генерирования катодных лучей Герца, могли дать прямое определение v, но такие эксперименты не кажутся осуществимыми.
Эксперименты Кауфмана могут одинаково объяснены модификацией существующих законов электродинамики до некоторой степени, что устраняет абсолютное движение и оставляя электродинамическую массу постоянной. Мы не можем вывести из этих экспериментов, что масса электронов электромагнитной природы, но это остается возможным и объединяющим природу физических сил в этой гипотезе. Какой бы замечательной вещью ни была теория, - эксперименты будут играть ту же важную роль.
Ссылки
Copyright © 1980, 2000 Robert S. Fritzius
Русский перевод Карима Хайдарова, 2003
|
|