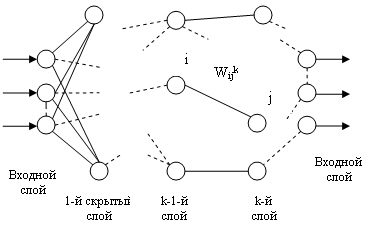
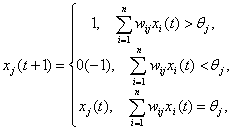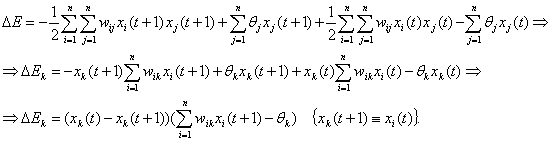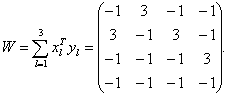В основе методов обучения многослойных нейросетей наиболее часто лежит так
называемое дельта-правило. Дельта-правило используется при обучении с учите
лем и реализуется следующим образом:
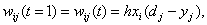
где h — параметр (шаг
обучения);
d — эталонное (требуемое) значение выхода
элемента.
Таким образом, изменение силы связей происходит в соответствии с
ошибкой выходного сигнала 5 = ( d — у) и уровнем
активности входного элемента х.. Обобщение дельта-правила , называемое
обратным распространением ошибки ( Back — propagation ), применимо к сетям с
любым числом слоев.
Обучение сети в этом случае состоит из следующих шагов:
1. Выбрать очередную обучающую пару ( х , d ). Подать входной вектор
на вход сети.
2. Вычислить выход сети у.
3. Вычислить
разность между выходом сети и требуемым выходом (ошибку).
4.
Подкорректировать веса сети так, чтобы минимизировать ошибку.
5.
Повторять шаги с 1-го по 4-й для каждой обучающей пары, пока ошибка
не
достигнет приемлемого уровня.
Ошибка функционирования сети обычно
определяется как
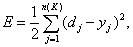
г де у j
= 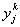 — выход сети.
— выход сети.
Для уменьшения этой ошибки следует изменить веса сети по правилу
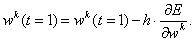
Эта формула описывает процесс градиентного
спуска в пространстве весов. Очевидно, для выходного слоя
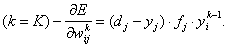
Т ак как
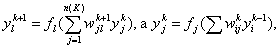
то для промежуточных
(скрытых)
слоев (то есть для
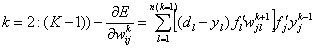
Если в качестве нелинейной преобразующей функции используется
сигмоидная функция, то удобно использовать рекуррентные формулы:
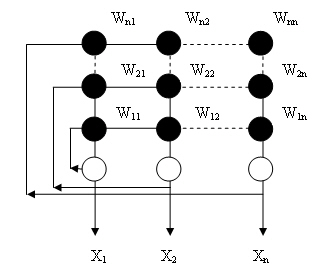
Рис. 13.4. Полносвязная сеть Хопфилда
Поскольку сигнал с выхода каждого
нейрона подается на входы всех остальных, >входной вектор начинает
циркулировать, преобразуясь по сети до тех пор, пока сеть не придет в устойчивое
состояние (то есть когда все нейроны на каждом пос ледующем цикле будут
вырабатывать тот же сигнал, что и на предыдущем). Оче видно, возможны
случаи бесконечной циркуляции входного вектора без достиже ния устойчивого
состояния.
Выберем функцию элементов в виде:
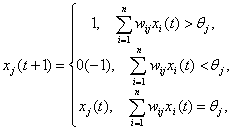
Состояние сети —
множество текущих значений сигналов
х от всех нейронов.
Функционирование сети геометрически может быть представлено как движение вектора
х , характеризующего состояние сети, на кубе [0,1]
п.
Когда подается но вый входной вектор, сеть переходит из вершины в вершину,
пока не стабилизиру ется. Устойчивая вершина определяется сетевыми весами,
текущими входами и величиной порога. Если входной вектор частично неправилен или
неполон, то сеть стабилизируется в вершине, ближайшей к желаемой.
В общем
случае все возможные состояния сети образуют некое подобие холмис той
поверхности, а текущие состояния сети аналогичны положениям тяжелого шарика,
пущенного на эту поверхность, — он движется вниз по склону в ближайший локальный
минимум. Каждая точка поверхности соответствует некоторому сочетанию активностей
нейронов в сети, а высота подъема поверхности в данной точке характеризует
«энергию» этого состояния. Энергия данного сочетания активностей определяется
как сумма весов связей между парами активных нейронов, взятая со знаком минус
(при 0 = 0).
Таким образом, если связь между двумя какимито нейронами имеет
большой положительный вес, то сочетания, в которых эти нейроны активны,
характеризуются низким уровнем энергии — именно к таким сочетаниям и будет
стремиться вся сеть. И, наоборот, нейроны с отрицательной связью при активации
добавляют к энергии сети большую величину, так что сеть стремится избегать
подобных состояний.
Динамику сети Хопфилда удобно описывать так называемой
функцией энергии, которая в достаточно общем виде может быть определена как
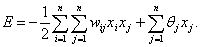
Функция энергии
определяет устойчивость сети, другими словами — это функ ция Ляпунова сети
Хопфилда , то есть функция, которая всегда убывает при изме нении состояния
сети. В конце концов эта функция должна достичь минимума и прекратить изменение,
гарантируя тем самым устойчивость сети.
Изменение состояния какого-либо
элемента сети всегда вызывает уменьшение энергии сети. Действительно, пусть
изменил свое состояние элемент
k ( k = 1 :
n ) , то есть его состояние изменилось с
+1 на 0 (или -1) или наоборот, тогда
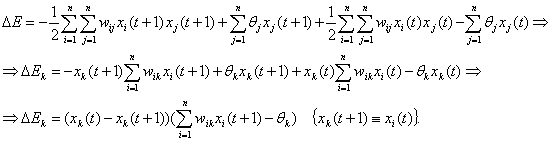
Видно, что в результате изменения
k -
ro элемента ∆
Ek ≤ 0, ∆
Ek = 0,, когда в сети не происходит никаких
изменений. Благодаря такому непрерывному стремлению к уменьшению энергия, в
конце концов, должна достигнуть минимума и прекра тить изменение. По определению
такая сеть является устойчивой. Сети Хопфил да называются также сетями,
минимизирующими свою энергию. Сети Хопфилда имеют многочисленные применения.
Некоторые из них связа ны со способностью этих сетей запоминать , а затем
восстанавливать даже по неполной входной информации различные образы. Другие
применения связаны с возможностью использования сетей Хопфилда для решения
оптимизационных задач.
13.6.3. Двунаправленная ассоциативная память
Основной причиной неудач исследователей в области искусственного
интеллек та, потративших свыше 20 лет на безуспешные попытки моделирования
интеллектуальной деятельности на базе обычных цифровых ЭВМ, является,
по-види мому, тот факт, что в современных ЭВМ существует прямая зависимость
времени поиска от количества хранимых образцов. Компьютер запоминает отдельные
объекты в отдельных ячейках, как бы заучивает сведения наизусть, и при
изуче нии наук примеры для него, в отличие от человека, отнюдь не полезнее
правил. НейроЭВМ , построенная на базе нейросетей , обладает ассоциативной
памятью и классифицирует поступившие образы со скоростью, которая не зависит от
коли чества уже поступивших образцов, — она немедленно связывает новый
образ с ближайшим имеющимся.
Память человека является ассоциативной — один
предмет напоминает нам о дру гом, а тот, в свою очередь о третьем и т. д. Наши
мысли как бы перемещаются от предмета к предмету по цепочке умственных
ассоциаций. Способность к ассоциа циям может быть использована для
восстановления забытых образов («мы с вами где-то встречались»).
Двунаправленная ассоциативная память является гетероассоциативной ; входной
вектор поступает на один набор нейронов, а соответствующий выходной вектор
вырабатывается на другом наборе нейронов. Как и сеть Хопфилда , двунаправлен ная
ассоциативная память способна к обобщению, вырабатывая правильные ре акции,
несмотря на возможные искажение входа.
Очевидно, состояние нейронов можно
рассматривать, как кратковременную память, так как она может быстро изменяться
при появлении другого входного вектора. В то же время значения коэффициентов
весовой матрицы образуют долговременную память (ассоциации) и могут изменяться
на более длительном отрезке време ни, используя соответствующий метод
обучения. Обучение производится с ис пользованием обучающего набора из пар
векторов х и у. Предположим, что все запомненные образцы представляют собой
двоичные векторы.
Решение задачи с помощью двунаправленной ассоциативной
памяти можно разбить на два этапа: режим обучения и непосредственно решение
(распознавание). Рассмотрим оба эти этапа на примере.
Каждый нейрон а.
в первом слое А имеет синапсы, соединяющие его с нейронами
Ь. во втором слое В. Пусть нейроны имеют следующий «смысл»: а, —
валюта, я2 — дол лары, а3 — марки, а4 —
рубли, bt — США, b 2
— Россия, b 3 —Канада, b
4 — Германия.
Режим обучения бинарными образами
Подадим на нейросеть три
бинарных связи ( x 1, y 1 ), ( x 2, y 2 ), ( x 3, y 3 ).
Пусть
x 1 = (1,1,0,0) → y 1 = (1,1,1,0);
x 2 = (1,0,1,0) →
у2 = (0,1,0,1);
x
3 = (1,0,0,1) → y 3 = (0,1,0,0);
Смысл
обучающих связей очевиден: если возбуждены нейроны a 1 и а 2
(в нашем распоряжении есть доллары), то по соответствующим синапсам
возбудятся ней роны b 1
, b 2 , b 3 (мы можем ими воспользоваться в США,
России и Канаде), и т. д. От бинарных связей перейдем к биполярным (это сделано
исключительно для про стоты, чтобы не нужно было вводить ненулевой порог
срабатывания нейронов):
x 1
= (1,1-1,-1) → y 1 =
( 1 ,1 -1,-1 );
x 2
= ( 1,-11,-1 → у2 = ( 1,-11,-1
x 3 = ( 1,-1-1,1 →
y 3 = ( 1,-1-1,1 ;
Составим матрицу весов:
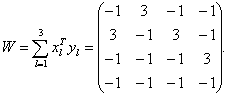
Режим распознавания Оценим эффективность запоминания обучающих
связей. Убедимся, что матрица W хранит связи ( x 1, y 1 ), ( x 2, y 2 ), ( x 3, y 3 ). Подадим на вход x 1 тогда x 1 = (2, 2, 2, -2) — это
означает, что в слое В возбудятся первые три нейрона (порог
срабатывания принят равным нулю). Тогда в бинарной форме у = (1, 1, 1,0),
что является требу емой ассоциацией. Это означает, что подача на вход x 1 , приводит к y 1, то есть ЭВМ
действительно «запомнила» связь ( x
1, y 1 ).
Аналогично проверяется запоминание остальных связей.
Сеть является
двунаправленной: y 1 W
T = (1, 5, -3, -3) → (1, 1, 0, 0) → x 1 , и т. д. Определим
энергию связей в памяти:
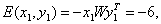
аналогично
Е( х2, у2) - 4 и
Е(х3 у3) = -2. Следует ожидать, что при ошибке в
исходной информации связь (
x 1,
y 1 ) будет
притягивать к себе больше образов, так как это точка устойчивого равновесия
с
минимальным энергетическим уровнем. Действительно, подадим на вход
образ
x ' = (1,1,0,1) — искажен
ный на один бит
x 1 и
х3 тогда
x ' W = (1,1,1, -3)→
(1,1,1,0) →
y 1 .
Аналогично, если взять
х " = (1, О, 1, 1) — вектор, расположенный
«между»
х 2 и
х3, то получим (-3, 1, -3, 1)
→ (0, 1, 0, 1) →
у2 — связь (
x 2, y 2 ) , притягивает к себе,
так как ее энер гия меньше энергии (
x 3, y 3 ).
Работа с
неопределенными данными. Рассмотрим случай, когда тип валюты неопределен x '-
(1,0, 0,0), тогда
x ' W = (-1, 3, -1, -1) → (0, 1,
0, 0) →
у3. Это означает, что она может быть использована
только в той стране, где в ходу любая валюта.
Если валюта может быть любой, например, доллары и марки, то она может исполь
зоваться везде:
x '-(1, 1, 1,0) → x 'М = (1, 1,1,1) → у’.
Проведенное исследование показывает, что построенная нейросеть способна за
помнить необходимую информацию на этапе обучения, а в рабочем режиме по зволяет
решать задачи распознавания, то есть реализует функции ассоциативной памяти. Вся
полученная при обучении информация сосредоточена в матрице W . За
счет параллельной структуры сеть решает задачу «мгновенно» — за одно дей
ствие — умножение входного вектора на матрицу памяти. Так как информация как бы
интегрирована в матрицу W , сеть способна достаточно эффективно
решать задачу и при частичных искажениях в исходных данных.
13.6.4. Самоорганизующиеся сети Кохонена
Характерной особенностью мозга является то, что его структура,
по-видимому ,, отражает организацию внешних раздражителей, которые в него
поступают. На пример, известно соответствие относительного положения
рецепторов на поверх ности кожи и нейронов в мозге, которые воспринимают и
обрабатывают сигналы от этих рецепторов, а участки кожи, которые плотно
«населены» рецепторами (лицо, руки), ассоциированы с пропорционально большим
числом нейронов. Это соответствие образует то, что называется соматотропической
( somatotropic ) кар той, которая отражает поверхность кожи в часть мозга —
соматосенсорную кору которая и воспринимает ощущение касания.
Системы, построенные на базе, например, многослойных сетей с обратным
распределением ошибок имеют очевидный недостаток, заключающийся в том, что мы
(как учитель) должны заранее заготовить входы и запастись соответствующи ми
правильными ответами для обучения сети. Принципы функционирования природной
соматотропической карты легли в основу создания самоорганизую щихся сетей
(карт, решеток) Кохонена , для которых не требуется предваритель ное
обучение на примерах. Сеть Кохонена воспринимает только вход и способна
вырабатывать свое собственное восприятие внешних стимулов.
Самоорганизующиеся сети Кохонена — это карты или многомерные решетки, d
каждым узлом которой ассоциирован входной весовой вектор, то есть набор из k
входных весов нейрона трактуется как вектор в ^- мерном пространстве.
(На рис. 13.5 представлена сеть при k = 2.) Входной весовой
вектор имеет ту же размерность, что и вход в сеть. Обучение происходит в
результате конкуренции, возникающей между узлами сети за право отклика на
полученный входной сигнал. Элемент сети, который выигрывает в этой конкуренции
(победитель), и его ближайшее окружение (свита) модифицируют веса своих входных
связей. Перед обучением каждая компонента входного весового вектора
инициализирую ется случайным образом. Обычно каждый вектор нормализуется в
вектор с единичной длиной в пространстве весов. Это делается делением
соответствующего веса на корень из суммы квадратов компонент этого весового
вектора. Входные вектора нормализуются аналогично. Обучение сети состоит из
следующих этапов:
1. Вектор х = (х 1 ,
х2,..., xk ) подается на вход сети.
2. Определяется расстояние dij (в k -мерном пространстве) между х и
весовыми векторами ij
каждого нейрона, например: dtj = 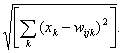
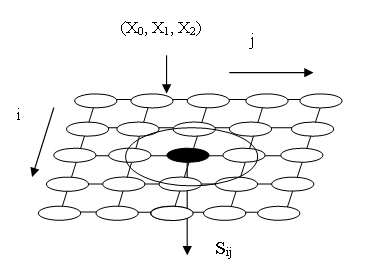
Рис. 13.5. Самоорганизующаяся карта Кохонена
3. Нейрон, который
имеет весовой вектор, самый близкий к х , объявляется
«победителем». Этот весовой вектор 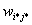 становится основным в группе входных весовых
векторов, которые лежат в пределах расстояния D от
становится основным в группе входных весовых
векторов, которые лежат в пределах расстояния D от 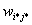 . Таким образом определяется "свита"
победителя.
. Таким образом определяется "свита"
победителя.
4. Группа
входных весовых векторов модифицируется (поощряется) в соответ ствии со
следующим выражением 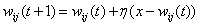 для всех
весо вых векторов в пределах расстояния D от
для всех
весо вых векторов в пределах расстояния D от 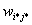 .
.
5.
Шаги 1 — 4 повторяются
для каждого входного вектора.
В процессе обучения значения D и
постепенно уменьшаются: η : 1 → 0, D в начале обучения
может равняться максимальному расстоянию между весовыми векторами, а к концу
обучения доходить до величины, при которой будет обучаться толь ко один
нейрон.
Из формулы адаптации входного весового вектора следует, что он (для
победите ля и его «свиты») сдвигается по направлению к входному вектору. Таким
обра зом, по мере поступления новых входных векторов весовые векторы сети
разде ляются на группы, формирующиеся в виде облаков (сгустков, кластеров)
вокруг входных векторов. По мере обучения плотность весовых векторов будет выше
в тех позициях пространства, где входные векторы появляются чаще, и наоборот. В
результате сеть Кохонена адаптирует себя так, что плотность весовых векторов
будет соответствовать плотности входных векторов. Так, если, например, на вход
сети подать поток равномерно распределенных случайных величин, то сетевые веса
будут самоприводиться в порядок в регулярную решетку. На рис. 13.6 приведен
пример самообучения двухмерной сети Кохонена .
ПРИМЕЧАНИЕ
В общем случае h = h (
r , t ), где г — расстояние между
нейронами, f — параметр, характеризую щий время обучения. Эта функция
традиционно имеет вид «мексиканской шляпы» (зависи мость силы связи от
расстояния до победителя), которая по мере увеличения параметра f делается более
узкой.
Обучающий алгоритм настраивает входные весовые векторы в окрестности
воз бужденного нейрона таким образом, чтобы они были более «похожими» на
вход ной вектор. Если все векторы нормализованы в векторы с единичной
длиной, то они могут рассматриваться как точки на поверхности единичной
гиперсферы . В процессе обучения группа соседних весовых точек перемещается
ближе к точке входного вектора.
Очевидно, так как S = 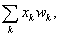 то победитель может быть
найден так:
то победитель может быть
найден так:
( i * , j * ) = arg max (
Sij ) — наиболее активный нейрон.
Самоорганизующиеся сети, как
уже отмечалось, не требуют предварительного обучения на примерах (учитель не
нужен) и используются в задачах распознава ния — классификации образов,
представленных векторными величинами, в которых каждая компонента вектора
соответствует элементу образа. После обучения подача входного вектора из данного
класса будет приводить к возбуждению нейронов; тогда нейрон с максимальным
возбуждением и будет представлять класси фикацию. Очевидно, в общем случае
можно формировать выход, зависящий как от активности победителя, так и от его
свиты. Так как обучение проводится без указания целевого вектора, то априори
невозможно определить, какой нейрон будет соответствовать данному классу входных
векторов. Однако после обучения такие соответствия легко идентифицируются и
могут быть использованы, напри мер, в задачах управления.
Знаете ли Вы, что в 1965 году два американца Пензиас (эмигрант из Германии) и Вильсон заявили, что они открыли излучение космоса. Через несколько лет им дали Нобелевскую премию, как-будто никто не знал работ
Э. Регенера, измерившего температуру космического пространства с помощью запуска болометра в стратосферу в 1933 г.? Подробнее читайте в
FAQ по эфирной физике.
НОВОСТИ ФОРУМА

Рыцари теории эфира | | 10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров.
10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров.
10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров.
10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров.
10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров.
10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров.
10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров.
10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров.
10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров.
10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров.
10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров.
10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.
|