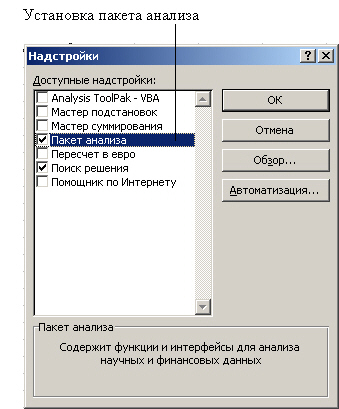
Если процесс установки Завершается успешно, то в меню Сервис появляется еще один пункт - Анализ данных (рис. 6.17), а также при создании формул становится доступной новая группа функций - статистические.
Проблема изучения взаимосвязей различного рода показателей является одной из
важнейших в экономическом анализе. В конечном счете, основное содержание любой
экономической политики может быть сведено к регулированию экономических переменных,
осуществляемому на базе выявленной тем или иным образом информации об их взаимовлиянии.
Целью статистического исследования является обнаружение и исследование соотношений
между статистическими (экономическими) данными и их использование для изучения,
прогнозирования и принятия решений.
Любые экономические данные представляют собой количественные характеристики
каких-либо экономических объектов. Они формируются под действием множества факторов,
не все из которых доступны внешнему контролю. Неконтролируемые факторы могут
принимать случайные значения из некоторого множества значений и тем самым обусловливать
случайность данных, которые они определяют. Стохастическая природа экономических
данных обусловливает необходимость применения специальных статистических методов
для их анализа и обработки.
Поэтому фундаментальными понятием статистического анализа являются понятия вероятности
и случайной величины.
Конечно, Excel не предназначен для комплексного статистического анализа и обработки
данных (в отличие от специального статистического программного обеспечения,
такого как STATISTICA, Eviews, TSP, SPSS, Microfit и др.). Однако и на базе
электронных таблиц можно провести некоторую статистическую обработку данных.
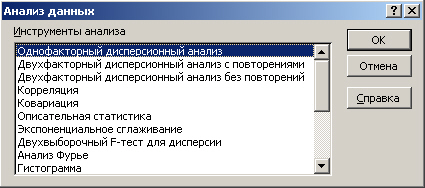
В частности, в рамках Excel с помощью команд, доступных из окна Анализ данных
(рис. 6.17), можно провести:
- описательный статистический анализ (Описательная статистика);
- ранжирование данных (Ранг и персентиль);
- графический анализ данных (Гистограмма);
- прогнозирование данных (Скользящее среднее, Экспоненциальное сглаживание);
- регрессионный анализ (Регрессия) и др.
Термин "регрессия" широко применяется в научной литературе для обозначения
так называемой статистической зависимости между двумя (несколькими) сериями
значений каких-либо величин. Определение "статистическая" предполагает,
что рассматриваемая зависимость реализуется как некоторая общая тенденция, от
которой возможны случайные отклонения в ту или иную сторону.
Практические методы определения параметров регрессии (или, как еще говорят,
регрессионного анализа) базируются на достаточно сложном математическом аппарате,
составляющем предмет таких дисциплин, как математическая статистика, многомерный
статистический анализ и др.
В табл. 6.2 приведены статистические функции, позволяющие пользователю реализовывать
операции регрессионного анализа (выявления зависимостей между рядами данных)
непосредственно на рабочем листе электронной таблицы.
Таблица 6.2. Статистические функции для регрессионного анализа
| Функция | Назначение функции и ее аргументы | Тип |
| ЛИНЕЙН | Определяет параметры линейного тренда для заданного
массива ЛИНЕЙН(знач.У; знач. X; констанста; стат.) |
Встроенная |
| ТЕНДЕНЦИЯ | Определяет предсказанные значения в соответствии
с линейным трендом для заданного массива (метод наименьших квадратов) ТЕНДЕНЦИЯ(знач.У; знач. X; новые знач.Х; константа;) |
Встроенная |
| ПРЕДСКАЗ | Определяет предсказанное значение функции в
заданной точке на основе линейной регрессии ПРЕДСКАЗ(Х; знач.У; знач. X) |
Встроенная |
| НАКЛОН | Определяет коэффициент для независимой переменной
в уравнении парной регрессии НАКЛОН(знач.У; знач. X) |
Встроенная |
| ОТРЕЗОК | Определяет отрезок, отсекаемый на оси ординат
линией линейной регрессии ОТРЕЗОК(знач.У; знач. X) |
Встроенная |
| КВПИРСОН |
Определяет квадрат коэффициента корреляции Пирсона |
Встроенная |
| ПИРСОН | Определяет коэффициент корреляции Пирсона (степень
линейной зависимости между двумя множествами данных) ПИРСОН(массив 1 ; массив 2) |
Встроенная |
| СТОШУХ | Определяет стандартную ошибку предсказанных
значений У для каждого X СТОШУХ(знач.У; знач. X) |
Встроенная |
| РОСТ | Аппроксимирует данные экспоненциальной кривой
РОСТ(знач.У; знач. X; новые знач.Х; константа;) |
Встроенная |
Перечисленные функции имеют очень широкий спектр экономических приложений. Например,
в качестве иллюстрации техники использования статистических функций Excel рассмотрим
задачу построения парной линейной регрессии между доходностью отдельно взятой
акции и доходностью рыночного портфеля.
Сформулированная проблема основывается на подходе к описанию поведения финансового
рынка с помощью так называемой модели САРМ. Не вдаваясь в подробности ее описания, заметим,
что одним из базовых ее допущений является предпосылка о возможности описания
связи между доходностью акции и доходностью рыночного портфеля с помощью уравнения.
Capital Asset Pricing Model (Модель оценки финансовых активов) (CAPM) - экономическая модель для оценки акций, ценных бумаг, деривативов и/или активов путем соотношения риска и ожидаемого дохода. CAPM основывается на той идее, что инвесторы требуют дополнительный ожидаемый доход (рисковую премию), если их просят взять на себя дополнительный риск.
Описание CAPM. Объяснение Capital Asset Pricing Model (Модель оценки финансовых активов).
CAPM была разработана Treynor ('61), Sharpe ('64) и Lintner ('65). Введя понятия систематического и специфического риска, она расширила теорию портфельного выбора (portfolio theory). В 1990, William Sharpe стал лауреатом Нобелевской премии по экономике. «За его вклад в теорию ценообразования финансовых средств, так называемую Capital Asset Pricing Model (Модель оценки финансовых активов) (CAPM).»
Модель CAPM утверждает, что ожидаемый доход, который потребуют инвесторы равен: ставке по безрисковой ценной бумаге плюс рисковая премия. Если ожидаемый доход не равен или выше, чем требуемая доходность, то инвесторы откажутся инвестировать, и инвестиции не будут сделаны.
CAPM анализирует портфельный риск в форме систематического риска (systematic risk) и специфического риска (specific risk). Систематическим риском обладает рыночный портфель (market portfolio). Когда происходят движения на рынке, каждый индивидуальный актив подвергается влиянию в той или иной степени. В той степени, в какой актив движется вместе с изменениями на рынке, он подвержен систематическому риску. Специфическим риском называется риск уникальный для индивидуального актива. Он представляет составляющую доходности актива, не взаимосвязанную с общими движениями на рынке.
Согласно CAPM, рынок компенсирует инвесторов за принятие систематического риска, но не за принятие специфического риска. Это потому, что специфический риск можно диверсифицировать. Когда инвестор держит рыночный портфель, каждый индивидуальный актив в портфеле подвержен специфическому риску. Но посредством диверсификации, чистая подверженность инвестора риску составляет лишь систематический риск рыночного портфеля.
Формула CAPM
Формула CAPM является следующей:
Ожидаемая доходность/Expected Security Return = Безрисковая доходность/Riskless Return + Beta x (Ожидаемая премия за рыночный риск/Expected Market Risk Premium)
или:
r = Rf + Beta x (RM - Rf)
{ Другой вариант формулы является следующим: r-Rf = Beta x (RM - Rf) }
где:
- r норма ожидаемого дохода по ценной бумаге;
- Rf ставка «безрисковой» инвестиции, т.е. по денежным средствам;
- RM норма доходности сопоставимого типа актива.
Beta - совокупный риск от инвестирования в общий рынок, как например, на Нью-Йоркской фондовой бирже. Beta, по определению приравнивается точно к 1.00000 .
Каждая компания также имеет Beta. Beta компании - риск компании по сравнению с Beta (риском) общего рынка. Если компания имеет Beta 3.0, то предполагается, что ее активы в 3 раза более рискованны, чем общий рынок. Beta показывает волатильность ценной бумаги, относительно типа актива.
Коэффициент Beta в данном уравнении (с точки зрения геометрической интерпретации
он является угловым коэффициентом графика) служит важнейшей характеристикой
риска изучаемого актива, о котором в зависимости от значения р можно заключить:
- Beta = 1 - риск ценной бумаги равен рыночному (рыночный риск - стандартное отклонение
доходности рыночного портфеля), а доходность изменяется точно так же, как и
рыночная;
-Beta>1 - риск ценной бумаги выше рыночного. В результате этого доходность ценой
бумаги изменяется в том же направлении, что и рыночная, но в большей степени.
Таким свойством, как правило, обладают ценные бумаги компаний, оперирующих в
энергично развивающихся высокотехнологичных отраслях;
- 0<Beta<1 - риск ценной бумаги ниже рыночного, а ее доходность изменяется
в том же направлении, что и рыночная, но в меньшей степени. Это часто встречается
у компаний в традиционных отраслях, особенно связанных с пищевой промышленностью
и коммунальным хозяйством;
- Beta<0 - данный теоретически возможный вариант означает, что доходность такой
ценной бумаги изменяется в направлении, противоположном изменению рыночной доходности.
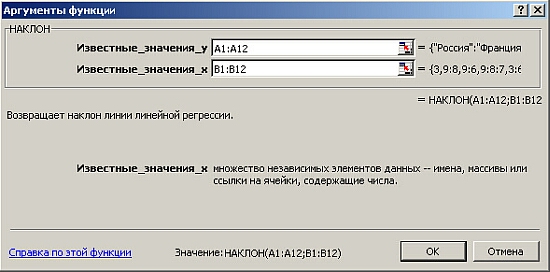
Если в качестве исходной информации мы имеем серии значений доходностей акций
и доходностей рыночного (индексного) портфеля по периодам, то, применяя функцию
НАКЛОН, мы можем легко получить оценку значения р-коэффициента (рис. 6.18).
Заметим, что для оценки значения свободного члена линейного уравнения (ос) применяется
функция ОТРЕЗОК.
В случае, если мы хотим провести полный статистический анализ имеющихся серий значений и, в частности, проверить статистические характеристики (значимость) полученных коэффициентов и всего уравнения регрессии в целом, нужно воспользоваться упомянутой выше надстройкой Пакет анализа (команда меню Пакет анализа > Регрессия).
|
|
 |