|
|
|
Кисть (canvas.Brush)
используется методами, обеспечивающими вычерчивание замкнутых областей, например
геометрических фигур, для заливки (закрашивания) этих областей. Кисть, как объект,
обладает двумя свойствами, перечисленными в табл. 10.5.
Таблица 10.5.
Свойства объекта TBrush (кисть)
|
Свойство |
Определяет |
||
|
Color Style |
Цвет закрашивания замкнутой области Стиль (тип) заполнения
области |
||
Область внутри контура
может быть закрашена или заштрихована. В первом случае область полностью перекрывает
фон, а во втором — сквозь незаштрихованные участки области будет виден фон.
В качестве значения
свойства Color можно использовать любую из констант типа TColor (см. список
констант для свойства Pen.color в табл. 10.2).
Константы, позволяющие
задать стиль заполнения области, приведены в табл. 10.6.
Таблица 10.6.
Значения свойства Brush, style определяют тип закрашивания
|
Константа |
Тип заполнения (заливки)
области |
||
|
bsSolid |
Сплошная заливка |
||
|
bsClear |
Область не закрашивается |
||
|
bsHorizontal |
Горизонтальная штриховка |
||
|
bsVertical |
Вертикальная штриховка |
||
|
bsFDiagonal |
Диагональная штриховка
с наклоном линий вперед |
||
|
bsBDiagonal |
Диагональная штриховка
с наклоном линий назад |
||
|
bsCross |
Горизонтально-вертикальная
штриховка, в клетку |
||
|
bsDiagCross |
Диагональная штриховка,
в клетку |
||
В качестве примера
в листинге 10.1 приведена программа Стили заполнения областей, которая
в окно (рис. 10.2) выводит восемь прямоугольников, закрашенных черным цветом
с использованием разных стилей.
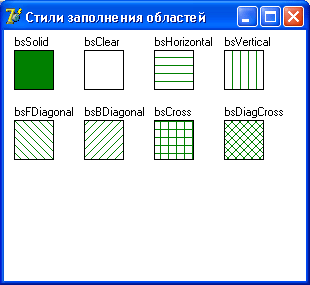
Рис. 10.2. Окно
программы Стили заполнения областей
Листинг 10.1.
Стили заполнения областей
unit brustyle_;
interface
uses
Windows, Messages, SysUtils, Classes,
Graphics,
Controls, Forms, Dialogs, ExtCtrls;
type
TForm1
= class(TForm)
procedure FormPaint(Sender: TObject);
private
{ Private declarations}
public
{ Public declarations )
end;
var
Form1:
TForm1;
implementation
{$R
*.DFM}
//
перерисовка формы
procedure
TForm1.FormPaint(Sender: TObject);
const
bsName:
array[1..8] of string =
('bsSolid','bsClear','bsHorizontal',
'bsVertical','bsFDiagonal','bsBDiagonal',
'bsCross','bsDiagCross');
var
x,y:
integer; // координаты левого верхнего угла прямоугольника
w,h:
integer; // ширина и высота прямоугольника
bs:
TBrushStyle;// стиль заполнения области
k:
integer; // номер стиля заполнения
i,j: integer;
begin
w:=40;
h:=40; // размер области(прямоугольника)
у:=20;
for
i:=l to 2 do
begin
х:=10;
for
j:=1 to 4 do
begin
k:=j+(i-1)*4; // номер стиля заполнения
case
k of
1:
bs = bsSolid;
2:
bs = bsClear;
3:
bs = bsHorizontal;
4:
bs = bsVertical;
5:
bs = bsFDiagonal;
6:
bs = bsBDiagonal;
7:
bs = bsCross;
8:
bs = bsDiagCross; end;
//
вывод прямоугольника
Canvas.Brush.Color := clGreen;
// цвет закрашивания — зеленый
Canvas.Brush.Style := bs;
// стиль закрашивания
Canvas
. Rectangle (x, y, x+w, y-t-h) ;
// вывод названия стиля
Canvas.Brush.Style
:= bsClear;
Canvas.TextOut(x, y-15, bsName[k]);
// вывод названия стиля
x := x+w+30;
end;
у := y+h+30;
end;
end;
end.
|
|
|
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|
 |
