Лекция 9. Физические модели баз данных

Рассмотрим файлы с плотным индексом. В этих файлах основная область содержит последовательность записей одинаковой длины, расположенных в произвольном порядке, а структура индексной записи в них имеет следующий вид:

Здесь значение ключа — это значение первичного ключа, а номер записи — это порядковый номер записи в основной области, которая имеет данное значение первичного ключа.

Так как индексные файлы строятся для первичных ключей, однозначно определяющих запись, то в них не может быть двух записей, имеющих одинаковые значения первичного ключа. В индексных файлах с плотным индексом для каждой записи и основной области существует одна запись из индексной области. Все записи в индексной области упорядочены по значению ключа, поэтому можно применить более эффективные способы поиска в упорядоченном пространстве.

Длина доступа к произвольной записи оценивается не в абсолютных значениях, а в количестве обращений к устройству внешней памяти, которым обычно является диск. Именно обращение к диску является наиболее длительной операцией по сравнению со всеми обработками в оперативной памяти. Наиболее эффективным алгоритмом поиска на упорядоченном массиве является логарифмический, или бинарный, поиск. Очень хорошо изложил этот алгоритм барон Мюнхгаузен, когда он объяснял, как поймать льва в пустыне. При этом все пространство поиска разбивается пополам, и так как оно строго упорядочено, то определяется сначала, не является ли элемент искомым, а если пет, то в какой половине его надо искать. Следующим шагом мы определенную половину также делим пополам и производим аналогичные сравнения, и т. д., пока не обнаружим искомый элемент. Максимальное количество шагов поиска определяется двоичным логарифмом от общего числа элементов в искомом пространстве поиска:

Однако в нашем случае является существенным только число обращений к диску при поиске записи по заданному значению первичного ключа. Поиск происходит в индексной области, где применяется двоичный алгоритм поиска индексной записи, а потом путем прямой адресации мы обращаемся к основной области уже по конкретному номеру записи. Для того чтобы оценить максимальное время доступа, нам надо определить количество обращений к диску для поиска произвольной записи.

На диске записи файлов хранятся в блоках. Размер блока определяется физическими особенностями дискового контроллера и операционной системой. В одном блоке могут размещаться несколько записей. Поэтому нам надо определить количество индексных блоков, которое потребуется для размещения всех требуемых индексных записей, а потому максимальное число обращений к диску будет равно двоичному логарифму от заданного числа блоков плюс единица. Зачем нужна единица? После поиска номера записи в индексной области мы должны еще обратиться к основной области файла. Поэтому формула для вычисления максимального времени доступа в количестве обращений к диску выглядит следующим образом:

Давайте рассмотрим конкретный пример и сравним время доступа при последовательном просмотре и при организации плотного индекса. Допустим, что мы имеем следующие исходные данные:

Длина записи файла (LZ) — 128 байт. Длина первичного ключа (LK) — 12 байт. Количество записей в файле (KZ) — 100000. Размер блока (LB) — 1024 байт.

Рассчитаем размер индексной записи. Для представления целого числа в пределах 100000 нам потребуется 3 байта, можем считать, что у нас допустима только четная адресация, поэтому нам надо отвести 4 байта для хранения номера записи, тогда длина индексной записи будет равна сумме размера ключа и ссылки на номер записи, то есть:

Определим количество индексных блоков, которое требуется для обеспечения ссылок на заданное количество записей. Для этого сначала определим, сколько индексных записей может храниться в одном блоке:

KIZB = LB/LI = 1024/16 = 64 индексных записи в одном блоке. Теперь определим необходимое количество индексных блоков: KIB = KZ/KZIB = 100000/64 = 1563 блока.

Мы округлили в большую сторону, потому что пространство выделяется целыми блоками, и последний блок у нас будет заполнен не полностью.

А теперь мы уже можем вычислить максимальное количество обращений к диску при поиске произвольной записи:

Т_поиска ⁼ log₂KIB + 1 = log₂1563 + 1 = 11 + 1 = 12 обращений к диску.

Логарифм мы тоже округляем, так как считаем количество обращений, а оно должно быть целым числом.

Следовательно, для поиска произвольной записи по первичному ключу при организации плотного индекса потребуется не более 12 обращений к диску. А теперь оценим, какой выигрыш мы получаем, ведь организация индекса связана с дополнительными накладными расходами на его поддержку, поэтому такая организация может быть оправдана только в том случае, когда она действительно дает значительный выигрыш. Если бы мы не создавали индексное пространство, то при произвольном хранении записей в основной области нам бы в худшем случае было необходимо просмотреть все блоки, в которых хранится файл, временем просмотра записей внутри блока мы пренебрегаем, так как этот процесс происходит в оперативной памяти.

Количество блоков, которое необходимо для хранения всех 100 000 записей, мы определим по следующей формуле:

И это означает, что максимальное время доступа равно 12500 обращений к диску. Да, действительно, выигрыш существенный.

Рассмотрим, как осуществляются операции добавления и удаления новых записей.

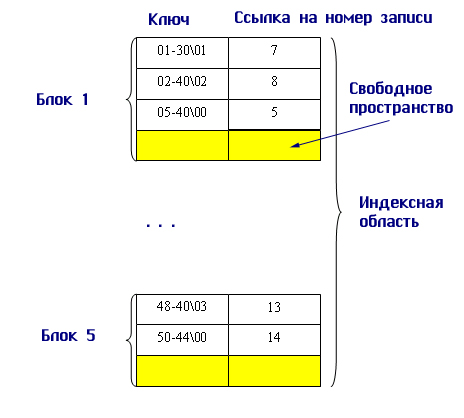
При операции добавления осуществляется запись в конец основной области. В индексной области необходимо произвести занесение информации в конкретное место, чтобы не нарушать упорядоченности. Поэтому вся индексная область файла разбивается на блоки и при начальном заполнении в каждом блоке остается свободная область (процент расширения) (рис. 9.7):

Рис. 9.7. Пример организации файла с плотным индексом

После определения блока, в который должен быть занесен индекс, этот блок копируется в оперативную память, там он модифицируется путем вставки в нужное место новой записи (благо в оперативной памяти это делается на несколько порядков быстрее, чем на диске) и, измененный, записывается обратно на диск. Определим максимальное количество обращений к диску, которое требуется при добавлении записи, — это количество обращений, необходимое для поиска записи плюс одно обращение для занесения измененного индексного блока и плюс одно обращение для занесения записи в основную область.

Естественно, в процессе добавления новых записей процент расширения постоянно уменьшается. Когда исчезает свободная область, возникает переполнение индексной области. В этом случае возможны два решения: либо перестроить заново индексную область, либо организовать область переполнения для индексной области, в которой будут храниться не поместившиеся в основную область записи. Однако первый способ потребует дополнительного времени на перестройку индексной области, а второй увеличит время на доступ к произвольной записи и потребует организации дополнительных ссылок в блоках па область переполнения.

Именно поэтому при проектировании физической базы данных так важно заранее как можно точнее определить объемы хранимой информации, спрогнозиро-вать ее рост и предусмотреть соответствующее расширение области хранения.

При удалении записи возникает следующая последовательность действий: запись в основной области помечается как удаленная (отсутствующая), в индексной области соответствующий индекс уничтожается физически, то есть записи, следующие за удаленной записью, перемещаются на ее место и блок, в котором хранился данный индекс, заново записывается па диск. При этом количество обращений к диску для этой операции такое же, как и при добавлении новой записи.

Знаете ли Вы, что релятивистское объяснение феномену CMB (космическому микроволновому излучению) придумал человек выдающейся фантазии Иосиф Шкловский (помните книжку миллионного тиража "Вселенная, жизнь, разум"?). Он выдвинул совершенно абсурдную идею, заключавшуюся в том, что это есть "реликтовое" излучение, оставшееся после "Большого Взрыва", то есть от момента "рождения" Вселенной. Хотя из простой логики следует, что Вселенная есть всё, а значит, у нее нет ни начала, ни конца... Подробнее читайте в FAQ по эфирной физике.


	Значение ключа	Номер записи

Файлы с плотным индексом, или индексно-прямые файлы