1. Введение

В 1992 Эндерс с соавторами продемонстрировал [1], что фотонное туннелирование происходит со сверхсветовой скоростью сигнала. Эксперименты были выполнены в микроволновом диапазоне. В то время какого-либо применения сверхсветового туннелирования не ожидалось несмотря на популярность полупроводникового туннелного диода. Десят лет спустя я собираюсь представить некоторые потенциальные приложения сверхсветового туннелирования в фотонике и электронике. Некоторые особенности кратковременных мод туннелирования и волнового механического туннелирования представлены в этом параграфе. В следующих параграфах существенные свойства сигнала, также как и универсальное время туннелирования будут представлены. Последующие параграфы посвящены приложениям процесса туннелирования и дано резюме о странных свойствах туннелирования.

Туннелирование - это механико-волновое представление кратковременных мод [2, 3]. Кратковременнные моды в основном находятся в маломерных волноводах, в запрещенных частотных полосах периодической гетероструктуре диэлектрика, а также в бипризмах в случае расстроенного полного отражения [4, 5]. Эти яркие примеры фотонных туннельных барьеров показаны на рисунке. 1. Диэлектрическая решетчатая структура эквивалентна электронной решетчатой структуре полупроводников с запрещенными энергетическими щелями.

Кратковременные моды и туннельные волновые функции характеризуются полностью мнимым волновым числом. Например, волновое уравнение для электрического поля E (z) дает

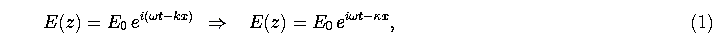
Где ω - угловая частота, t время, x интервал, k волновое число, и к мнимое волновое число кратковременной моды.

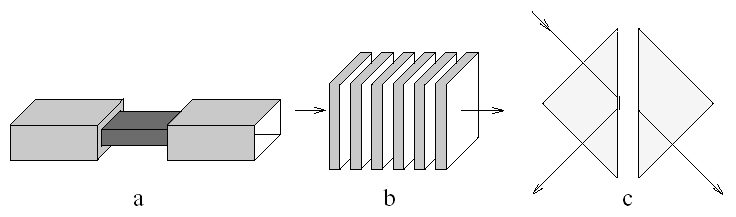
Рисунок 1. Эскиз трех явных фотонных барьеров. а) иллюстрирует маломерный волновод (центральная часть волновода имеет поперечное сечение меньше, чем половина длины волны в обоих перпендикулярных направлениях к распространению), b) фотонная решетчатая структура (периодический диэлектрик гетероструктуры), и c) расстроенное полное внутреннее отражение бипризмы, где полное отражение происходит на границе от более плотной к менее плотной диэлектрической среде.

В трех приведенных примерах моды характеризуются экспоненциальным ослаблением передачи из-за отражения фотонными барьерами и недостаточным сдвигом фаз внутри барьера. Последнее означает нулевое время преодоления барьера согласно фазо-временного подхода.

Где τ, φ, ω, являются фазовым временем, фазой, и угловой частотой, соответственно. Наблюдаемое очень короткое время туннелирования вызвано свойствами фронта барьера. Здесь время туннелирования будет определено как время группы или время затрачиваемое сигналом на пересечение барьера.

Время измерялось вне барьера детекторами, установленными впереди и сзади барьера. Это время соответствует фазово-временной групповой задержке, см., например, ссылки [6, 7, 8].

На рисунке 2 дан набросок импульса (то есть волнового пакета), который представляет собой цифровой сигнал. Фронт пакета очень плавный, соответственно узкой полосе занимаемых им частот. Частотная полоса менялась в зависимости от барьера, рассматриваемого так, что импульс содержит по существу лишь короткоживущие частотные компоненты. Такой короткоживущий импульс перемещается за нулевое время через непрозрачные барьеры, что в свою очередь приводит к бесконечной скорости при фазово-временнном подходе, пренебрегающем сдвигом фаз во фронте барьера [1, 9].

В обзоре квантово-механического туннелирования проблема времени снова рассмотрена Коллинзом и другими [10], которые утверждают следующее:

"Фазово-временной результат первоначально полученный Вигнером и Хартманом является лучшим приближением для использования в широком диапазоне параметров барьеров, энергий и волновых пакетов".

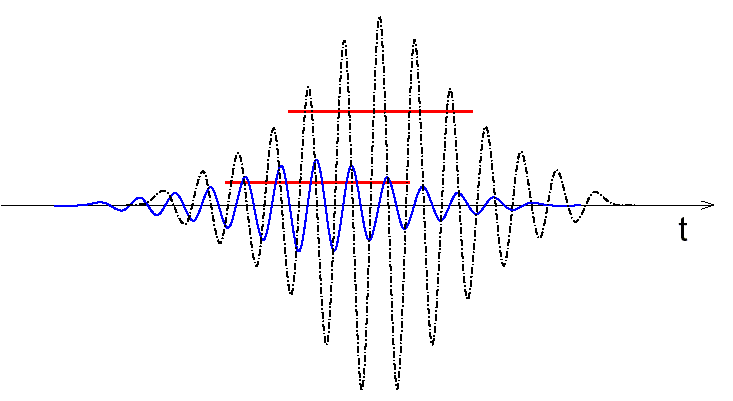
Рисунок 2. Амплитудо-временнная эпюра двух волновых пакетов (то есть импульсов). Большой пакет перемещался медленнее, чем малый. Горизонтальные полосы указывают половину ширины пакетов и не зависят от величины пачки. Эпюра иллюстрирует постепенно начало пакетов.

Передний фронт пакета может быть описан , например, соотношением

[1-exp (-t/τ)] [sin (τt)]

где τ - временная константа.

Эйнштейнова причинная связь запрещает сверхсветовую скорость сигнала в вакууме и в средствах с реальным показателем преломления. Это правило не соблюдается для сред, характеризующихся мнимым показателем преломления, где сдвиг фаз равен нулю, как в случае короткоживущих мод. Чтобы избежать искажения сигнала из-за дисперсии особых сред, сигнал должен быть ограничен в частотной полосе. Проблема ограниченной частотной полосы и ограничении длительности сигналов была обсуждена и объяснена квантово-механическими аргументами в [11, 12]. Фактически, сигналы ограниченной частотной полосы и ограниченной длительности передаются в мультиплексной телефонии уже более ста лет. Теория для этих технических сигналов и еще более общая для всех физических сигналов, представляется теоремой отсчетов (Теоремой Котельникова), которая была введена в практику Шенноном около 50 лет назад [13]. Более подробно о свойствах сигналов представлено в параграфе "Сигналы".

Короткоживущие моды - это решения классических уравнений Максвелла, однако, они проявляют некоторые неклассические свойства, как например:

1. По всей видимости короткоживущие моды представлены нелокальными полями, как это было предсказано и позже показано передачей и частичным отражением в экспериментах [4, 9, 14]. Туннелирование и время отражения равны и независимы от длины барьера.
2. Короткоживущие моды имеют отрицательную энергию и, таким образом, они не могут быть измерены [15, 16].
3. Короткоживущие моды могут быть описаны виртуальными фотонами [17].
4. Короткоживущие моды не являются лоренцевым инвариантом, так как имеет место
   (v_φ/c)²→ ∞, где v' = x/τ - фазовая скорость и c - скорость света в вакууме, а x - длина барьера.

Очевидно, что короткоживущие моды не полностью поддаются описанию максвелловскими уравнениями, и здесь должны быть учтены квантово-механические аспекты.

Этот случай аналогичен фотоэффекту, который был объяснен Эйнштейном с позиций квантовой механики, то есть фотонами. В общем случае электрические поля обнаружимы только квантовым обменом энергией.

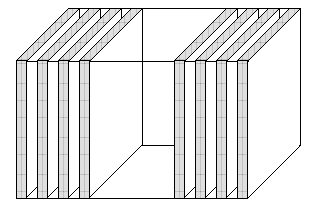
Рисунок 3. Пример резонансной электромагнитной туннельной структуры, решенной с помощью короткоживущих мод (запрещенных частотных полос) в области микроволновых частот. Две периодические четвертьволновые гетероструктуры из плексигласа и воздуха, которые отделены интервалом 18.9 см, формирующим резонансную полость, с полной длиной 30 см.

Задержка туннелирования, которая возникает на передней поверхности непрозрачных барьеров, является постоянной величиной и независит от толщины барьера. Таким образом с увеличивающейся толщиной барьера скорость сигнала увеличивается в той же самой пропорции, что и длина. Это явление часто называется эффектом Хартмана [18, 19].

Эффективная толщина барьера может быть значительно увеличена на резонансных барьерных структурах без уменьшения пропускания. Резонансные туннельные структуры на запрещенных частотных полосах выгодны для скоростных узкополосных сигналов [4, 20]. Рисунок 3 показывает резонансный барьер, построенный из двух фотонных барьеров на решетчатых структурах.

Дисперсионные отношения для соответствующих коэффициентов передачи и скорости сигналов в периодических диэлектрических четвертьволновых гетероструктурах показаны в Рис. 4.

Рисунок 4. Диаграмма (a) показывает дисперсионное отношение для резонансной гетероструктуры в зависимости от частоты (Рис. 3 (a)). Передаточная дисперсия периодической гетероструктуры показывает запрещенные щели, разделенные резонансными пиками. Запрещенные частотные щеои соответствуют режиму туннелирования, подробнее см. в [4]. Короткоживущий режим характеризуется сильным ослаблением из-за отражения. В (b) показана групповая (сигнальная) скорость в единицах с для резонансной периодической диэлектрической четвертьволновой гетероструктуры в зависимости от частоты.

Поскольку узкая частотная полоса ограничивает сигналы, то не имеется никакого значительного дисперсионного эффекта, если несущая частота помещена в центр запрещенной частотной щели. Каждый из трех барьеров, показанных на рисунке 1, имеет различное дисперсионное отношение. Один из них описывает расстроенное полное внутреннее отражение бипризмы. В этом случае проходящее электрическое поле и мнимое волновое число к дается соотношениями [3]:

Где θ - угол падающего луча света, E₀ электрическое поле на входе барьера, n₁ и n₂ - показатели преломления, и (n₁/n₂sinθ > 1. Коэффициент передачи t = E_t/E₀ как функция воздушного зазора бипризмы был измерен в микроволновом диапазоне и показан на рисунке 5. Показанные данные находятся в согласии с уравнениями (3), (4).

Время туннелирования в случае расстроенного полного внутреннего отражения (РПВО) было повторно исследовано недавно [21, 22]. Однако, в теоретическом описании поведения времени РПВО имеется тот недостаток, что он основан на рассмотрении лишь идеально плоских волн. Этот подход пригоден для неограниченного диаметра луча, но не вписывается должным образом в методику опыта с ограниченными диаметрами луча [22, 23].

В настоящей работе описано два простых эксперимента, которые демонстрируют сверхсветную скорость сигнала в фотонных барьерах. Сигнал представлен импульсом, как те, что используется в цифровых системах связи [11, 16]; один эксперимент был проведен в микроволновом диапазоне, а другой - в инфракрасном частотном диапазоне, как это показано на рисунках 6, 7.

Цифровой сигнал, показанный на рисунке. 6 туннелируется с шириной полосы частот меньше, чем 10^-2 на скорости 8c. Несущая частота составляла 9.15 GHz. Старт обнаружения огибающей туннелированного сигнала - приблизительно на 0.8 ns ранее, чем таковой для сигнала по воздуху. Частотная полоса сигнала содержит по существу только короткоживущие сомпоненты. Экспериментальное устройство для определения и демонстрации сверхсветовой групповой скорости показано на рисунках 8 и 9. Прибытие группы волн было измерено в вакууме, где групповая, энергеническая и сигнальная скорости равны c [24, 25], (фактически, свойства сигнала не зависят от его амплитуды, как это показано на рисунке 2). Амплитудное модулирование микроволн с частотой 9.15 GHz (λ=3.28 cm) производилось свип-генератором HP8341B (10 MHz - 20 GHz). Параллельный луч передавался параболической антенной. Переданный сигнал принимался другой параболической антенной, выпрямлялся диодом (HP8472A (NEG)) и выводился на осциллограф (HP54825A).

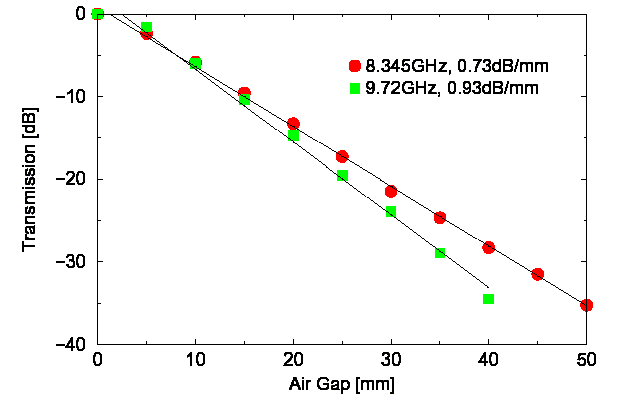
Рисунок 5. Передача сигнала через воздушный зазор, измеренная на двух частотах [22]. Данные соответствуют теоретическим соотношениям (3), (4).

Время распространения сигнала было измерено по воздушному промежутку между передатчиком и приемником и по тому же самому промежутку, но частично, заполненому барьером 28-ми сантиметровой длины. Структура барьера формировалась четвертьволновыми плитками из плексигласа, показанными на рисунках 3, 4 и рассмотренными ранее. Каждая пластина 0.5 см толщины, а интервал между двумя плитками - 0.85 см. Две структуры отделены воздушным интервалом 18.9 см, формирующим резонансную туннельную структуру [4]. При сравнении этих двух времен пробега мы видим, что туннелированный сигнал прибыл к детектору приблизительно на 900 ps ранее, чем тот импульс, который шел тем же самым путем через воздух. Результат соответствует скорости импульса туннелированного сигнала 8·c.

Выполненные измерения были асимптотическими. Не было никакой связи между процессом генерации, процессом детектирования и фотонным барьером. Кроме того эксперимент не был стационарным, и сигнал измерен в дисперсии свободного вакуума. Экспериментальное окружение - то же самое, что и в интерферометре Хонг-У-Манделя, в котором измерение также является асимптотическим и выдает групповую, энергетическую и сигнальную скорости в одно и то же время [12, 26]. Эксперимент по измерению сверхсветовой скорости сигнала в инфракрасном диапазоне показан на рисунке 7.

До сих пор мы обсуждали только эксперименты по передаче. Экспериментальная установка для измерения частичного отражения фотонными барьерами на микроволновых частотах представлена на рисунке 9. Процедура варьирования длины барьера в таком эксперименте показана на рисунке 10.

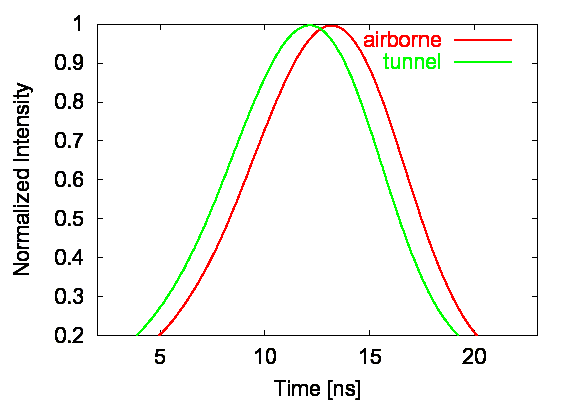
Рисунок 6. Измеренное время распространения двух сигналов. Более быстрый был туннелирован через запрещенную щель в фотонном барьере длиной 28 cm. Величины импульсо нормализованы. Туннелированный сигнал (полуширина импульса представляла один бит) пересекал барьер более, чем на 800 ps быстрее чем воздушный сигнал. Соответствующая этому времени скорость туннелируемого сигнала была 8·c.

2. Сигналы

Для примера, сигналом может быть фотон, который возбуждается атомом с хорошо известной энергией и поляризацией, или это может быть слово, сообщаемое приемнику. Оба примера описываются волновыми пакетами ограниченной полосы частот и ограниченной продолжительности. Огибающая фотона также, как огибающая такого слова распространяется со скорости света в вакууме. В вакууме групповая и энергетическая скорости сигнала равны c. Физические и, конечно, все технические сигналы подобны тем, что показаны на рисунках 6, 7, 11 - ограниченной полосы частот. Технические сигналы модулируются по амплитуде (AM) или по частоте (FM). Определения ширины полосы частот, длительности, и произведения интервала на полосу частот объяснены, например, в [29]. Частотные компоненты сигнала вне полосы частот, отвечающей гипотетическому фронту сигнала, обычно менее -60 dB по сравнению с пиковым значением сигнала. Локализация энергии Фурье-преобразования в полосе частот ограничивает сигналы по скорости распространения и времени и, следовательно, по поведению, нарушающему причинность. Однако, компоненты, нарушающие причинность никогда не обнаруживались. В случае неограниченной полосы частот волновой пакет представлен аналитической функцией, и информация, содержащаяся во фронте пакета, определяет весь пакет [30]. Это математически правильно, но не уместно для сигналов с физической точки зрения.

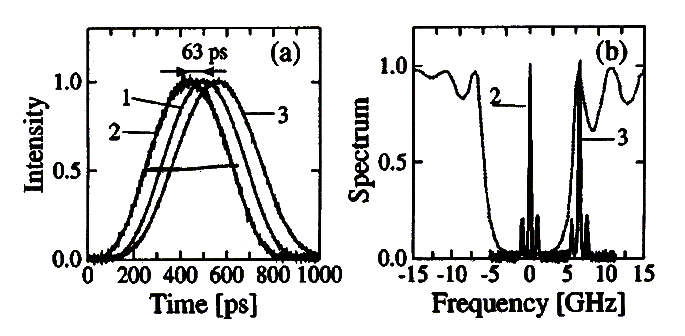
Рисунок 7. Измеренное время распространения трех цифровых сигналов [35]. (а) Траектория импульса 1 была зарегистрирована в вакууме. Импульс 2 пересекал фотонную решетчатую структуру в центре щели полосы частот (см. часть (b) рисунка), а импульс 3 был зарегистрирован для импульса, прошедшего по стекловолокну вне щели запрещенной зоны. Фотонная решетчатая структура представляла собой периодическую диэлектрическую гетероструктуру из стекловолокна.

Как отмечено выше, инженеры передавали сигналы ограниченной полосы частот и ограниченной продолжительности по мультиплексной технологии уже сотню лет назад. Историческая картинка такой мультиплексной системы передачи данных показана на рисунке 12. Очевидно, пять сигналов, переданных по одному проводу - это ограниченная частотная полоса и ограниченная длительность сигнала. В этом примере ширина полосы частот была 2 кГц, а длительность составляла приблизительно 0.3 мс. Шеннона и многие другие исследователи и теоретики выдали в результате, что произведение частотной полосы на длительность представляет количество информации. Фурье-преобразование такой мультиплексной схемы нарушает причинность. Это показывает, что временных компонент, нарушающих причинность в результате применения Фурье-преобразования не обнаруживается [11, 12].

3 универсальных времени туннелирования

Анализ данных о времени туннелирования, полученных в различных экспериментах с непрозрачными барьерами, (то есть при кz > 1) указывает на существование универсального времени [31]. Отношение

найденное независимо от частоты и типа барьера, было изучено в [31, 32], где τ, η и T - время туннелирования, несущая частота или энергия волнового пакета W относящиеся через константу Планка h, и T - время колебания волны. Микроволновые эксперименты вблизи 10 GHz показали время туннелирования приблизительно 100 ps, эксперименты в оптическом частотном диапазоне на 427 THz показали время туннелирования 2.2 fs. В работе [31] было предположено, что это отношение соблюдается также для волновых пакетов с массой покоя, имея в виду математическую аналогию между уравнениями Гельмгольца и Шрёдингера. Квантово-механические исследования указывают на правильность этой догадки [9, 10, 33]. Недавно время туннелирования электрона было измерено в эксперименте по автоэлектронной эмиссии [34]. Измеренные времена составили величины между 6 fs и 8 fs. Принимая энергию электрона 0.6 eV (высота барьера 1.7 eV), эмпирическое уравнение (5), получим время туннелирования 7 fs.

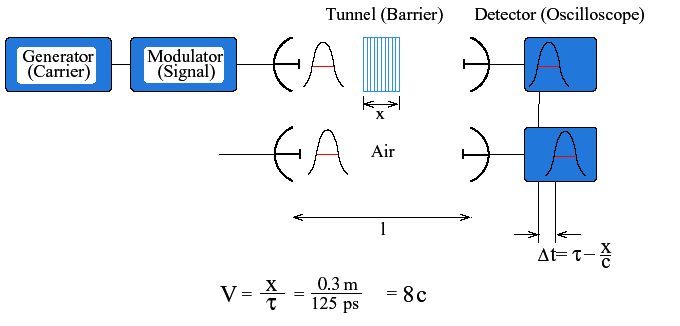
Рисунок 8. Экспериментальное устройство на периодической диэлектрической геретроструктуре из четвертьволновых элементов для измерения групповой скорости, то есть скорости сигнала.

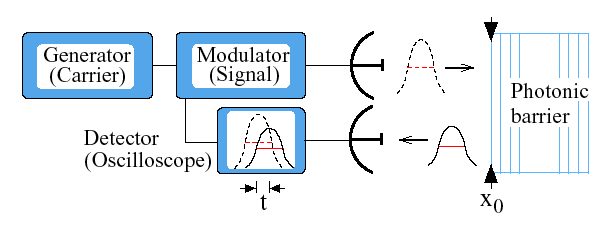
Рисунок 9. Экспериментальное устройство на периодической структуре из четвертьволновых диэлектрических элементов для измерения частичного отражения как функции длины барьера.

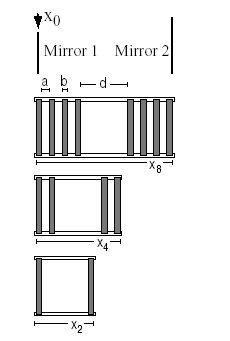
Рисунок 10. Методика опыта измерения частичного отражения сигнала в зависимости от строения фотонной решетки.

4. Приложения в фотонике

Туннельная передача имеет экспоненциальное уменьшение сигнала с глубиной барьера, потерь передачи из-за отражения. Фактически, потерянная энергия не диссипируется в теплоту и может быть возвращена повторными циклами в специально спроектированных схемах.

4.1 Туннелирование

a) Недавно Лонги и другие [35] выполнили туннелирование узкополосных инфракрасных импульсов на расстояние 20 тысяч длин волн, соответствующее приблизительно 80 тысячам слоев четвертьволновых элементов.

Их результаты представлены на рисунке 7. Полная длина оптоволоконной решетчатой структуры была 2 см (в масштабе длины барьера для 10 GHz микроволновый барьер был бы 400 м длиной). Периодическая вариация показателя преломления по стекловолокну между двумя различными слоями четвертьволновых отрезков составляла величину порядка 10^-4. Измеренная групповая скорость была 2c, а коэфициент передачи барьера был 1.5 %.

b) Аналогичный туннельный барьер 16.81 м. длиной находится в стадии изготовления в Университете Кобленца. Длинная структура предназначена для микроволновых сигналов на частоте 9.15 GHz, то есть на длине волны 3.28 cm. 159 диэлектрических слоев, отличающихся по показателю преломления от 1.00 (воздух) до 1.05 (пластик). Время передачи огромного барьера будет составлять 14 нс по сравнению с временем в вакууме 56 нс. Ожидаемая скорость сигнала будет 4c с коэффициентом передачи 0.16 % [36]. Туннелируемый сигнал достигнет детектора на 49 нс ранее, чем он же в воздухе.

4.2 Частичное отражение фотонными барьерами

Отражение фотонного барьера было испытано на длине волны 1.5 µm в волоконной оптике. Барьеры выполнены как 2 см стекловолокна со слабо периодически изменяемым показателем преломления, подобным барьеру, использованному в эксперименте по сверхсветовой передачи Лонги и других, описанном в [35]. Потери на отражение фотонным барьером (мнимый импеданс) меньше чем таковые металла. Фотонные барьеры представляют собой более эффективные зеркала, чем металл. Например фотонные барьеры эффективно используются для стабилизации инфракрасных лазерных диодов в оптоэлектронике.

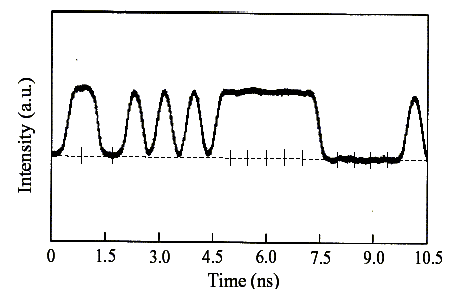
Рисунок 11. Сигналы: измеренный сигнал в произвольных единицах измерения. Половина ширины в блоках 0.2 нс соответствует числу битов. Слева направо: 1,1,0,0,1,0,1,0,1,0,1,1,1,1,1,1,1, ..... инфракрасная несущая частота сигнала 2·10¹⁴ Hz (длина волны 1.5 µm). - ширина полосы частот сигнала - приблизительно 2·10¹⁰ Hz отношение к несущей частоте 10^-4 [27].

b) Рисунок 13 показывает время - зависимые данные об отражении двумя зеркалами в различных положениях и фотонными барьерами различных длин. Изменяется иолько величина отраженного импульса, но не отражательное время с длиной барьера. Наблюдаемое отражательное время приблизительно 100 пс эквивалентно времени туннелирования в барьерной передаче. Нелокальное поведение мод туннелирования дает информацию относительно длины барьера в пределах времени одного колебания на фронте барьера.

Нами разработан ультрабыстрый модулятор на основе частичного отражения. Эффективная длина барьера модулируется электрическим полем вынуждающим изменение показателя преломления в половину полной длины барьера. Это приводит к амплитудному изменению отражения, см. рис. 13. Другой тип модуляции может быть получен путем локального изменения показателя преломления сигналами, возбуждающими оптически активную диэлектрическую среду. Например, этот принцип применялся в экспериментах с отрицательной групповой скоростью, см. например, работу [38]. В случае вышеупомянутого микроволнового эксперимента модуляции на расстоянии 15 см от входа барьера появляются во фронте барьера в пределах 100 пс, принимая во внимание, что соответствующее время распространения света в пять раз более медленное.

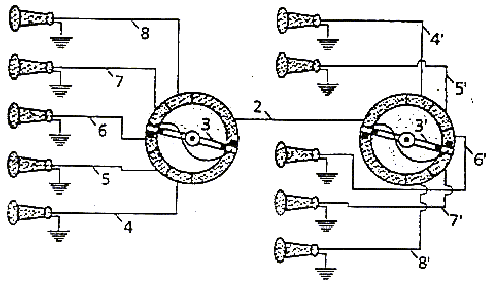
Рисунок 12. Историческая картина системы мультиплексной передачи [28].

5. Приложения в электронике

5.1. Туннельные диоды

Первым туннельным устройством, сделанным человеком, был туннельный диод. Он был изобретен Есаки около 1960. Это нелинейное электронное устройство все шире используется начиная с того самого времени. Однако, время туннелирования, которое дало бы окончательную динамическую характеристику такого диода, все же никогда не было измерено. Наша догадка: универсальное время фотонного туннелирования [31] имеет силу также для процесса туннелирования электронов. Фактически, недавние эксперименты по туннелированию электронов поддерживают эту догадку [34]. Экспериментальные данные находятся в согласии с отношением уравнения (6).

5.2. Сверхсветовая передача электронов

Как показано в нескольких квантово-механических исследованиях, например, Лоу и Менде, частица, перемещающаяся через длинный, высокий барьер, существенно локализована в пространстве и времени так, как будто это тунеллирование за нулевое время. [33]. Конечно, рассматривалось только время, необходимое на преодоление внутренней части барьера. Снова, как и в случае фотонного туннелирования скорость обхода барьера была сверхсветовой даже в случае релятивистского подхода [10, 33, 37].

Движение электронов в полупроводнике довольно медленно по сравнению с скоростью света. Предельная самая высокая скорость электрона приписывается баллистическим электронам подобно случаю с электронным микроскопом или некоторыми полупроводниковыми структурами нано-устройств.

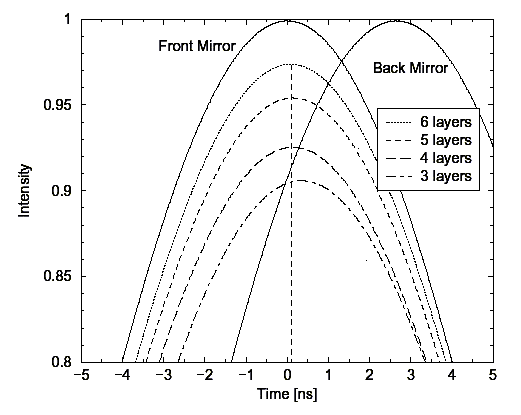
Рисунок 13. Измеренные частично отраженные микроволновые импульсы ко времени. Параметр - композиция барьера, как показано на рисунке 10. Показаны отражения сигналов от металлических зеркал или от фронта барьера или обратной стороны [14]. В этом примере длина волны была 3.28 см, а эффективная длина барьера - 41 см.

Напряжение на электронных устройствах имеет порядок 1V. Это приводит к баллистической скорости электронов порядка 10⁶ м/с, что на два порядка меньшее чем c.

5.2.1 Структуры на электронных решетках

Мы предлагаем структуру на электронной решетке с чередующимися слоями четвертьволновых элементов различной шириной запрещенной зоны, которая может быть пересечена на сверхсветовой скорости. Длина волны электрона зоны проводимости имеет порядок 1 нм. Ультрабыстрая связь электронных элементов устройства в цепи может исполнять роль ускорителя скорости компьютеров. Например, периодическая структура из четвертьволновых элементов Si/SiGe представляет электронную решетчатую структуру. Такое легирование структуры Si-полупроводника сплавом SiGe дает небольшую вариацию ширины щели, аналогично периодической диэлектрической оптоволоконной структуре, упомянутой выше. Электронная структура может иметь протяженность до 1 µm и может использоваться в роли ультра-быстрого соединения между элементами устройства.

5.2.2 pn-туннельный переход

Туннелирование через барьер классического туннельного диода также может быть использовано для быстрых электронных соединений. Соответствующим легированием профиля путь туннелирования, можно регулировать его длину приблизительно от 100 нм до нескольких тысяч нанометров.

Однако, имеется проблема, не решенная всеми туннельными приложениями - это высокое отражение на входе барьера. Однако, туннелирование - не диссипативный процесс с диссипацией энергии. Отраженная электронная мощность должна использоваться в цикле грамотным проектированием интегральных микросхем.

6. Выводы

Процессы туннелирования показывают удивительные свойства в случае непрозрачных барьеров, к которым мы не привыкли в классической физике. Время туннелирования универсально и возникает на фронте барьера. Оно равняется приблизительно обратно несущей частоте или энергии волнового пакета, деленной на постоянную Планка h. Для преодоления барьера волновой пакет не тратит никакого времени. Это свойство приводит к сверхсветовым сигнальной и энергетической скоростям. Последнее стало очевидным в однофотонном эксперименте, где детектор измеряет сверхсветовую энергетическую скорость фотона [39]. Другой странный опыт состоит в том, что короткоживущие моды поля не поддаются описанию уравнениями Максвелла полностью. Например, они несут энергию диссипации, которая делает невозможным их обнаружение [15, 16, 40], и они нелокальны. В частности, их свойства в согласии с механико-волновым туннелированием. Это аналогично тому, как в атоме водорода и в фотоэмиссии, где квантовая механика необходима для объяснения стабильности атома и взаимодействии электрона и фотона. Энергия сигналов всегда конечна, что приводит к ограниченному спектру частот. Это есть следствие планковского квантования радиации с энергетическим минимумом hω [11]. Электрическое поле не может быть измерено непосредственно. Все детекторы нуждаются по крайней мере в одном кванте энергии hω, чтобы сработать. Это есть фундаментальная неточность классической физики, которая манипулирует с любым малым количеством поля и заряда.

Физический сигнал не имеет явного фронта огибающей. Последнее нуждалось бы в бесконечно высокочастотных компонентах и, соответственно, в бесконечной энергии [6, 12]. Кроме того сигналы не могут бвть представлены аналитической функцией, иначе полная информация содержалась бы во фронте сигнала [30]. Другое следствие ограничения частотной полосы сигналов состоит в том, что если они имеют только короткоживущие моды, они могут нарушать эйнштейнову причинную связь, которая утверждает, что сигнальная и энергетическая скорости <= c. Несмотря на такое широкое обсуждение нарушения эйнштейновой причинной связи [5], все свойства, введенные выше полезны для новых быстрых устройств, как в фотонике, так и в электронике. Согласно Коллинзу и другим [10] споры о нулевом времени туннелирования (время пересечения внутренней части барьера) излишни после прочтения работ Вигнера и Хартмана. Обсуждения относительно сверхсветового туннелирования напоминают мне проблеме мультиплексной передачи, показанной на рисунке 12. Здесь продолжительность конечного промежутка времени сигнала и ограничение частотной полосы нарушают причинную связь согласно Фурье-преобразования. Однако, ни один телефон не звонит прежде, чем другой телефон будет включен. Это указывает на критическую роль конечных частотных полос и продолжительность конечного промежутка времени сигналов без того, чтобы нарушить принцип причинности связи [12].

7. Благодарности

Я с благодарностью подтверждаю обсуждение настоящей работы с A. Хейбелем, A. Стальхофеном, и Р.-М. Веттер.

Ссылки

Перевод с английского - Карим Хайдаров, Bourabai Research, 2007