 .
.На занятии 2 уже шла речь о таких программах. Программы линейной структуры: присвоение значений переменным, производство вычислений, вывод результатов. Цель занятия: развить и закрепить умения составлять несложные программы линейных структур, с тем, чтобы эти умения успешно применять при разработке более сложных конструкций. Повторите содержание предыдущих занятий.
Учимся на конкретных, ярких примерах.
Вначале составим программы с комментариями. Внимательно разберитесь в каждом символе этих программ, задайте вопросы.
1.Дана прямая ax + by + c = 0 и точка с координатами x0; y0. Найти расстояние от точки до прямой по формуле  .
.
************************Программа 4.1***********************************
PRINT”Дано общее уравнение прямой ax + by + c = 0”
INPUT”Введите коэффициенты a, b, c”;a, b, c
INPUT”Введите координаты точки x,y”;x0, y0
d = ABS(a*x0 + b*y0 + c)
r = SQR(a^2 + b^2)
PRINT”Искомое расстояние равно”; d/r
2. По введенным катетам прямоугольного треугольника вычислить площадь, гипотенузу, высоту, проведенную из вершины прямого угла на гипотенузу, и острые углы. Значения углов выразить в градусах и минутах.
************************Программа 4.2***********************************
PRINT”По традиции а и b – катеты, с - гипотенуза”
INPUT”Введите катеты a, b”;a, b
с = SQR(a^2 + b^2):’***Вычислили гипотенузу***********
s = a*b/2:’***Вычислили площадь***********
h = a*b/c:’***Вычислили высоту***********
ta = а/b:’***Нашли тангенс угла А***********
ua = ATN(ta) :’***Вычислили угол А в радианах***********
ub = pi/2 – ua:’****Вычислили угол В радианах*******
uag = 180*ua/pi:’**Градусная мера угла А в десятичной записи
uac = int(uag):’****Градусы – целая часть*******
mina = cint((uag-uac)*100):’****Целое число минут угла А***********
‘******Аналогично определяем градусы и минуты угла В********
ubg = 180*ub/pi:’**Градусная мера угла B в десятичной записи
ubc = int(ubg):’****Градусы – целая часть*******
minb = cint((ubg-ubc)*100):’****Целое число минут угла B***********
‘**Выводим ответы****************
PRINT”Гипотенуза”; c
PRINT”Площадь”; s ; “кв. ед.”
PRINT”Высота”; h
PRINT”Угол А”;uac;” градусов “;mina; “минут”
PRINT”Угол B”;ubc;” градусов “;minb; “минут”
3.Дана функция y = f(x), значение аргумента x0 и приращение аргумента D x. Найти приращение функции. Как помните из курса математики
D f(x0) = f(x0 + D x) – f(x0)
Для контрольного примера введем функцию:
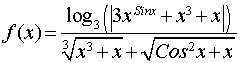
************************Программа 4.3***********************************
DEF FNA(x) = …проделайте это самостоятельно……
?”Введите х0”;: INPUN x
?”Введите приращение”;:INPUN h
f1 = DEF FNA(x + h): f2 = DEF FNA(x)
?”Приращение”; f1 – f2
4. Дано значение синуса аргумента первой четверти. Вычислить значения других тригонометрических функций.
************************Программа 4.4**********************************
?”Введите значение синуса, помните, что 0 < Sinx < 1”;: INPUN s
c = SQR(1- s^2)
t = s/c: ct = 1/t
?”Записывайте”
?”Косинус”;с
?”Тангенс”; t
?”Котангенс”; ct
5.Две точки на плоскости заданы своими координатами. Найти расстояние между ними.
************************Программа 4.5**********************************
INPUN “Введите координаты первой точки x1,y1”; x1,y1
INPUN “Введите координаты второй точки x2,y2”; x2,y2
d = SQR((x2 – x1)^2 + (y2 – y1)^2))
?”Расстояние между точками”; d
6.Решить систему двух линейных уравнений с двумя неизвестными методом Крамера.
************************Программа 4.6**********************************
REM***Здесь коэффициенты при неизвестных и свободный член первого уравнения******
DATA 3,5,-7
REM***Здесь коэффициенты при неизвестных и свободный член второго уравнения******
DATA 1,8,12
READ a1,b1,c1,a2,b2,c2
d = a1*b2 – a2*b1: dx = c1*b2 – c2*b1: dy = c2*a1 – a2*c1
x = dx/d: y = dy/d
?”Записывайте решение”; x,y
Следующие задачи рассмотрите самостоятельно и программы в электронном виде представьте на проверку преподавателю.
7.Два вектора заданы своими координатами. Найти их скалярное произведение и угол между ними.
8.Составить программу, которая бы спрашивала имя пользователя и здоровалась с ее обладателем.
9.Вычислить площадь поверхности и объема цилиндра. Известен радиус и высота цилиндра.
10.Известна длина окружности L. Найти площадь круга, ограниченного этой окружностью.
11.Найти площадь кольца, внутренний радиус которого равен r1, а внешний r2
12.Размеры комнаты axb, высота 2,3м. Дверь и окна занимают 15% площади стен. Комнату необходимо оклеить обоями, при оклейке 10% идут на обрезки. Размеры рулона обоев 10х0,7м. Сколько рулонов обоев необходимо приобрести, чтобы оклеить комнату?
13.Составить программы перевода одних единиц в другие, если: 1 дюйм = 2.54 см., 1 доллар = 29.78 руб.,1 миля = 1.609 км.
Задача 14 для домашней работы.
14.Треугольник задан длинами своих сторон. Найти его площадь по формуле Герона, высоты по формуле ha = ![]() , медианы по формуле ma =
, медианы по формуле ma = ![]() , биссектрисы по формуле
, биссектрисы по формуле
ta = ![]() , радиус описанной окружности R =
, радиус описанной окружности R = ![]() , радиус вписанной окружности r =
, радиус вписанной окружности r = ![]() .
.
А теперь выполните письменную самостоятельную работу и представьте на проверку.
Вычислить значение функции при заданном пользователем значении аргумента. Вариант (t,p,z,q,m,w) укажет преподаватель.
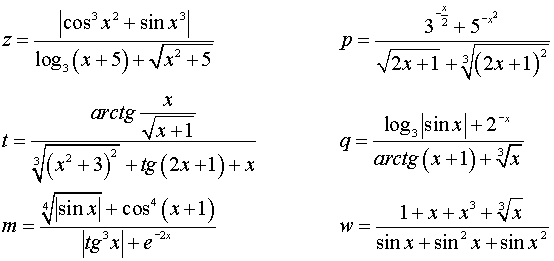
Чему Вы научились на занятии №4 ?
|
|